Question: (12 points, suggested time 25 minutes)
A group of students design an experiment to investigate the relationship between the density and pressure of a sample of gas at a constant temperature. The gas may or may not be ideal. They will create a graph of density as a function of pressure. They have the following materials and equipment.
- A sample of the gas of known mass Mg in a sealed, clear, cylindrical container, as shown
- above, with a movable piston of known mass mp
- A collection of objects each of known mass mo
- A meterstick
(a)
i. Describe the measurements the students should take and a procedure they could use to collect the data needed to create the graph. Specifically indicate how the students could keep the temperature constant. Include enough detail that another student could follow the procedure and obtain similar data.
ii. Determine an expression for the absolute pressure of the gas in terms of measured quantities, given quantities, and physical constants, as appropriate. Define any symbols used that are not already defined.
iii. Determine an expression for the density of the gas in terms of measured quantities, given quantities, and physical constants, as appropriate. Define any symbols used that are not already defined.
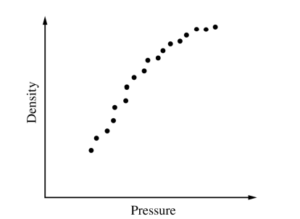
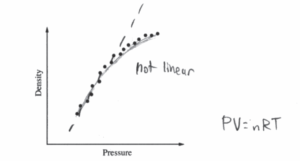
iv. The graph above represents the students’ data. Does the data indicate that the gas is ideal?
Describe the application of physics principles in an analysis of the graph that can be used to arrive at your answer.
Another group of students propose that the relationship between density and pressure could also be obtained by filling a balloon with the gas and submerging it to increasing depths in a deep pool of water.
(b) Why could submerging the balloon to increasing depths be useful for determining the relationship between the density and pressure of the gas?
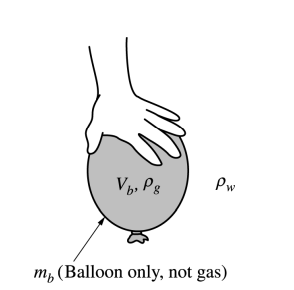
(c) The balloon is kept underwater in the deep pool by a student pushing down on the balloon, as shown above. Let Vb represent the volume of the inflated balloon, mb represent the mass of just the balloon (not including the mass of the gas), pg represent the density of the gas in the balloon, and pw represent the density of the water. Derive an expression for the force the student must exert to hold the balloon at rest under the water, in terms of the quantities given in this part and physical constants, as appropriate.
▶️Answer/Explanation
Ans:
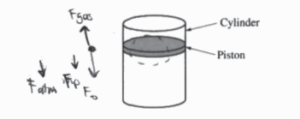
(a)
i.
The temperature should remain constant if the container remains sealed and away from direct sunlight. Place objects on to the piston one at a time. Density will be Mg divided by the current volume of the gas (πr2h, r and h measured by meter stick). Pressure is equal to the added weight of the piston and objects divided by the area of the piston. Graph density as a function of pressure and repeat with different numbers of objects.
ii.
\(P_{0}=\frac{F_{atm}}{A}\)
Fatm = P.A
\(P = \frac{F}{A}= \frac{F_{p}+nF_{0}+P_{0}A}{\pi r^{2}}\)
\(\frac{g(m_{p}+m_{0})+P_{0}\pi r^{2}}{\pi r^{2}}=P\)
r = radius of piston
P0 = atm pressure
iii.
\(P = \frac{m}{V}\)
\(P = \frac{Mg}{\pi r^{2}h}\)
r = radius of piston
h = height of piston
iv.
The graph shows that density 2 is proportional to pressure. In an ideal gas, pressure in inversely proportional to volume, and volume is inversely proportional to density. Therefore, in an ideal gas, density should be directly proportional to pressure. Since this is not the case for this gas, this gas is not an ideal gas.
(b)
The pressure of the water increases with depth, which would decreases the volume (increasing the density since density is inversely proportional to volume) because of the pressure difference. This allows volume and density to be varied and graphed.
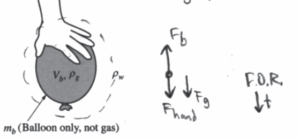
(c)
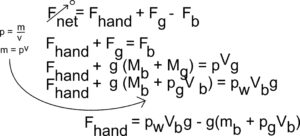
Question
An air bubble is formed at the bottom of a swimming pool and then released. The air bubble ascends toward the surface of the pool.
(A) In a clear, coherent, paragraph-length response, describe any changes in the bubble size and describe the motion of the bubble as it ascends to the surface. Explain the factors that affect the size of the bubble and the bubble’s motion. Include a description of any forces acting on the bubble from the time it is at the bottom of the pool until the bubble is just below the surface of the pool.
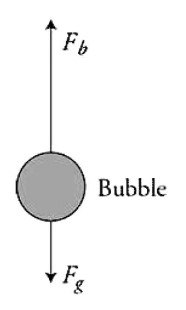
(B) On the figure, draw a vector for each force acting on the bubble. Make sure all vectors are drawn in correct proportion to each other.

(C) The bubble does not collapse under the pressure of the water. Explain how the behavior of the gas atoms keeps the bubble from collapsing.
(D) The bubble begins at a depth of D below the surface of the water where the bubble has an initial volume of \(V_{D}\). The atmospheric pressure at the surface of the pool is \(\rho\). The density of the water in the pool is \(P_{S}\). Assume that the air temperature in the bubble remains constant as it rises to the surface. Derive an expression for the volume (\(V_{S}\)) of the bubble when it reaches the surface of the pool.
(E) In part (D) it was assumed that the temperature of the bubble remains constant. Now assume that the air temperature in the bubble can change but that the bubble rises so quickly to the surface that there is negligible thermal energy transfer between the bubble and the swimming pool water. Base your answers on this assumption.
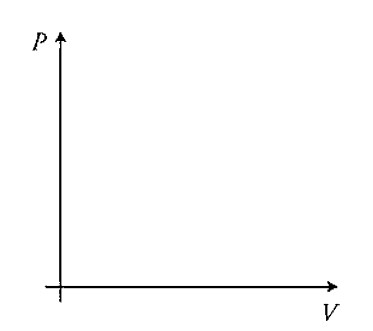
I. Sketch the process on the PV diagram. Indicate on the axis the initial and final pressures and volumes.
II. How does the value \(P_{S}V_{S}\) compare to the value \(P_{D}V_{D}\)?
_Greater than \(P_{D}V_{D}\) _Equal to \(P_{D}V_{D}\) _Less than \(P_{D}V_{D}\)
Justify your answer.
▶️Answer/Explanation
Ans:
Part (A)
The amount of air inside the bubble remains the same during ascent. The external pressure from the water on the bubble decreases as the
bubble rises. The bubble increases in volume as it moves upward. As the bubble volume increases, the buoyancy force increases, but the gravity force on the bubble remains constant. The bubble accelerates upward at an increasing rate as it ascends.
Part (B)
For buoyancy force upward and gravity force downward. Buoyancy must be drawn larger than gravity. If extra vectors are drawn, this point is not awarded.
Part (C)
The atoms inside the gas collide with and bounce off the water molecules. This causes a change in momentum of the gas atoms. This generates an equal and opposite force between the water and gas that keeps the bubble from collapsing.
Part (D)
For the correct relationship between the pressure at the surface of the water and at a depth D: \(P_{D}=P_{S}+\rho gD\)
For the correct application of the ideal gas law and the correct final expression:
\(P_{S}V_{S}=P_{D}V_{D}\)
\(P_{S}V_{S}=(P_{S}+\rho gD)V_{D}\)
\(V_{S}=\frac{(P_{S}+\rho gD)V_{D}}{P_{S}})
Part (E)
(i) 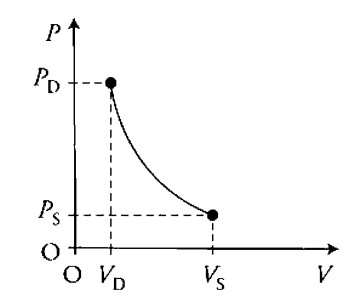
(ii) The process is an adiabatic expansion. There is no heat transfer between the water and the bubble. Therefore: \(Q=0\), and \(\Delta U=W\). Since the work is negative as the bubble expands, the internal energy of the bubble must also decrease. Therefore, the temperature and the PV value must also decrease.
Question
In the laboratory, you are given a cylindrical beaker containing a fluid and you are asked to determine the density ρ of the fluid. You are to use a spring of negligible mass and unknown spring constant k attached to a stand. An
irregularly shaped object of known mass m and density D (D >> ρ) hangs from the spring. You may also choose from among the following items to complete the task.
• A metric ruler
• A stopwatch
• String
(a) Explain how you could experimentally determine the spring constant k.
(b) The spring-object system is now arranged so that the object (but none of the spring) is immersed in the unknown fluid, as shown. Describe any changes that are observed in the spring-object system and explain why they occur.
(c) Explain how you could experimentally determine the density of the fluid.
(d) Show explicitly, using equations, how you will use your measurements to calculate the fluid density ρ. Start by identifying any symbols you use in your equations.

▶️Answer/Explanation
Ans:
a) Example 1: Measure the unstretched length of the spring. Hang it with the object at rest and measure the stretched length. Call the difference in these lengths ∆x. Equating the weight of the object and the force exerted by the extended spring gives mg = k∆x from which k can be determined.
Example 2: Set the hanging mass into oscillation. Determine the period T by timing n oscillations and dividing that time by n. The equation T = 2π√ m / k can then be used to find k. b) The spring is stretched less when the object is at rest in the fluid. The fluid exerts an upward buoyant force on the object. Since the net force on the object is still zero, the spring does not need to exert as much force as before and thus stretches less.
c&d)
1) Measure the length of the spring when the object is immersed in the liquid, and subtract the unstretched length to determine the amount the spring is stretched. This will allow calculation of the force exerted by the spring on the object.
2) The volume of fluid displaced is equal to the volume of the object, which can be determined from the given mass and density of the object.
3) The buoyant force on the object is equal to the difference of the object’s weight and the force exerted by the spring.
4) The buoyant force also equals the weight of the displaced fluid, which equals the product of the fluid density, displaced volume, and g.
Symbol Quantity
ρ fluid density
V object volume = displaced water volume
g acceleration of gravity
m mass of object
x spring stretch in air
xw spring stretch in water
First solving for k in air. mg = kx
Then in the fluid. Fsp = kxw
Fnet = 0 Fb = mg – Fsp ρVg = mg –kxw ρVg = mg – (mg / x) xw solve for ρ
