Question
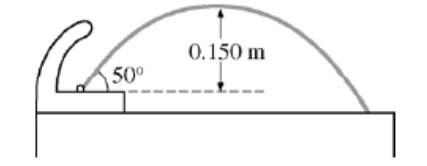
A drinking fountain projects water at an initial angle of 50° above the horizontal, and the water reaches a maximum height of 0.150 m above the point of exit. Assume air resistance is negligible.
(a) Calculate the speed at which the water leaves the fountain.
(b) The radius of the fountain’s exit hole is 4.00 x 10-3 m. Calculate the volume rate of flow of the water.
(c) The fountain is fed by a pipe that at one point has a radius of 7.00 x 10-3 m and is 3.00 m below the fountain’s opening. The density of water is 1.0 x 103 kg/m3 . Calculate the gauge pressure in the feeder pipe at this point.
▶️Answer/Explanation
Ans:
a) Using projectile methods. vfy2 = viy2 + 2ady 0 = (visin50)2 + 2(–9.8)(0.15) vi = 2.24 m/s
b) Volume flow rate = Q = Av = π(4×10–3)2 (2.24) = 1.13×10–4 m3/s
c) If you don’t understand the wording, here is what the problem is saying
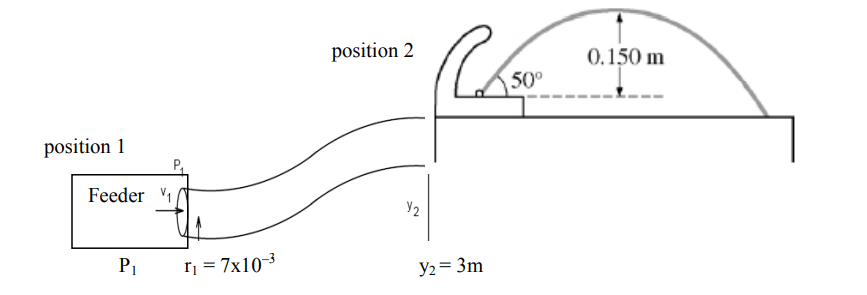
First we need to find the velocity of the water at the feeder using continuity
A1v1 = Q2 π(7×10–3)2(v1) = 1.13×10–4 v1 = 0.73 m/s
Bernoulli. Position 2 is the fountain spigot which is open so at atmospheric pressure. y1=0 no height.
P1 + ρgy1 + ½ ρv12 = P2 + ρgy2 + ½ ρv22
P1 + 0 + ½ (1000)(0.73)2 = (1.01×105) + (1000)(9.8)(3m) + ½ (1000)(2.24)2
P1 = 1.32×105 Pa which is the absolute pressure of the feeder.
To find the gauge pressure of the feeder. Pabs = Pgauge + Po 1.32×105 = Pgauge + 1.01×105
Pgauge = 31600 Pa.
Note: This gauge pressure could be determined directly in Bernoulli’s equation by realizing that P1 includes atmospheric pressure as part of its total value and that P2 was equal to atmospheric pressure, so by elimination of the term P2, P1 becomes the gauge pressure. This should be stated in the solution if it is the chosen solution method.
Question
An air bubble is formed at the bottom of a swimming pool and then released. The air bubble ascends toward the surface of the pool.
(A) In a clear, coherent, paragraph-length response, describe any changes in the bubble size and describe the motion of the bubble as it ascends to the surface. Explain the factors that affect the size of the bubble and the bubble’s motion. Include a description of any forces acting on the bubble from the time it is at the bottom of the pool until the bubble is just below the surface of the pool.
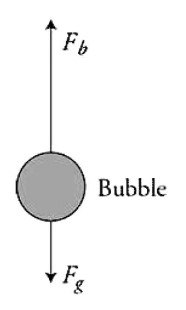
(B) On the figure, draw a vector for each force acting on the bubble. Make sure all vectors are drawn in correct proportion to each other.

(C) The bubble does not collapse under the pressure of the water. Explain how the behavior of the gas atoms keeps the bubble from collapsing.
(D) The bubble begins at a depth of D below the surface of the water where the bubble has an initial volume of \(V_{D}\). The atmospheric pressure at the surface of the pool is \(\rho\). The density of the water in the pool is \(P_{S}\). Assume that the air temperature in the bubble remains constant as it rises to the surface. Derive an expression for the volume (\(V_{S}\)) of the bubble when it reaches the surface of the pool.
(E) In part (D) it was assumed that the temperature of the bubble remains constant. Now assume that the air temperature in the bubble can change but that the bubble rises so quickly to the surface that there is negligible thermal energy transfer between the bubble and the swimming pool water. Base your answers on this assumption.
I. Sketch the process on the PV diagram. Indicate on the axis the initial and final pressures and volumes.
II. How does the value \(P_{S}V_{S}\) compare to the value \(P_{D}V_{D}\)?
_Greater than \(P_{D}V_{D}\) _Equal to \(P_{D}V_{D}\) _Less than \(P_{D}V_{D}\)
Justify your answer.
▶️Answer/Explanation
Ans:
Part (A)
The amount of air inside the bubble remains the same during ascent. The external pressure from the water on the bubble decreases as the
bubble rises. The bubble increases in volume as it moves upward. As the bubble volume increases, the buoyancy force increases, but the gravity force on the bubble remains constant. The bubble accelerates upward at an increasing rate as it ascends.
Part (B)
For buoyancy force upward and gravity force downward. Buoyancy must be drawn larger than gravity. If extra vectors are drawn, this point is not awarded.
Part (C)
The atoms inside the gas collide with and bounce off the water molecules. This causes a change in momentum of the gas atoms. This generates an equal and opposite force between the water and gas that keeps the bubble from collapsing.
Part (D)
For the correct relationship between the pressure at the surface of the water and at a depth D: \(P_{D}=P_{S}+\rho gD\)
For the correct application of the ideal gas law and the correct final expression:
\(P_{S}V_{S}=P_{D}V_{D}\)
\(P_{S}V_{S}=(P_{S}+\rho gD)V_{D}\)
\(V_{S}=\frac{(P_{S}+\rho gD)V_{D}}{P_{S}})
Part (E)
(i) 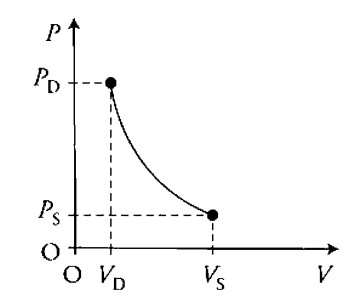
(ii) The process is an adiabatic expansion. There is no heat transfer between the water and the bubble. Therefore: \(Q=0\), and \(\Delta U=W\). Since the work is negative as the bubble expands, the internal energy of the bubble must also decrease. Therefore, the temperature and the PV value must also decrease.
Question
An air bubble is formed at the bottom of a swimming pool and then released. The air bubble ascends toward the surface of the pool.
(A) In a clear, coherent, paragraph-length response, describe any changes in the bubble size and describe the motion of the bubble as it ascends to the surface. Explain the factors that affect the size of the bubble and the bubble’s motion. Include a description of any forces acting on the bubble from the time it is at the bottom of the pool until the bubble is just below the surface of the pool.
(B) On the figure, draw a vector for each force acting on the bubble. Make sure all vectors are drawn in correct proportion to each other.

(C) The bubble does not collapse under the pressure of the water. Explain how the behavior of the gas atoms keeps the bubble from collapsing.
(D) The bubble begins at a depth of D below the surface of the water where the bubble has an initial volume of \(V_{D}\). The atmospheric pressure at the surface of the pool is \(\rho\). The density of the water in the pool is \(P_{S}\). Assume that the air temperature in the bubble remains constant as it rises to the surface. Derive an expression for the volume (\(V_{S}\)) of the bubble when it reaches the surface of the pool.

(E) In part (D) it was assumed that the temperature of the bubble remains constant. Now assume that the air temperature in the bubble can change but that the bubble rises so quickly to the surface that there is negligible thermal energy transfer between the bubble and the swimming pool water. Base your answers on this assumption.
I. Sketch the process on the PV diagram. Indicate on the axis the initial and final pressures and volumes.
II. How does the value \(P_{S}V_{S}\) compare to the value \(P_{D}V_{D}\)?
_Greater than \(P_{D}V_{D}\) _Equal to \(P_{D}V_{D}\) _Less than \(P_{D}V_{D}\)
Justify your answer.
▶️Answer/Explanation
Ans:
Part (A)
The amount of air inside the bubble remains the same during ascent. The external pressure from the water on the bubble decreases as the
bubble rises. The bubble increases in volume as it moves upward. As the bubble volume increases, the buoyancy force increases, but the gravity force on the bubble remains constant. The bubble accelerates upward at an increasing rate as it ascends.
Part (B)
For buoyancy force upward and gravity force downward. Buoyancy must be drawn larger than gravity. If extra vectors are drawn, this point is not awarded.

Part (C)
The atoms inside the gas collide with and bounce off the water molecules. This causes a change in momentum of the gas atoms. This generates an equal and opposite force between the water and gas that keeps the bubble from collapsing.
Part (D)
For the correct relationship between the pressure at the surface of the water and at a depth D: \(P_{D}=P_{S}+\rho gD\)
For the correct application of the ideal gas law and the correct final expression:
\(P_{S}V_{S}=P_{D}V_{D}\)
\(P_{S}V_{S}=(P_{S}+\rho gD)V_{D}\)
\(V_{S}=\frac{(P_{S}+\rho gD)V_{D}}{P_{S}})
Part (E)
(i) 
(ii) The process is an adiabatic expansion. There is no heat transfer between the water and the bubble. Therefore: \(Q=0\), and \(\Delta U=W\). Since the work is negative as the bubble expands, the internal energy of the bubble must also decrease. Therefore, the temperature and the PV value must also decrease.
