Question
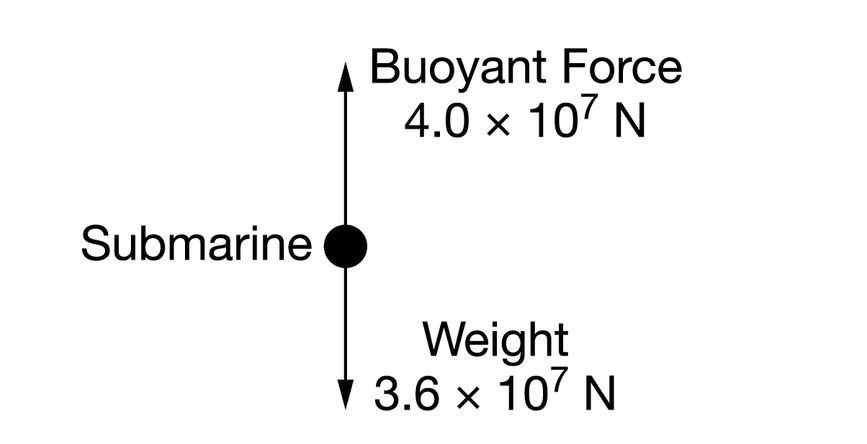
A submarine of mass \(3.6×10^6\)kg is submerged in water and at equilibrium. Inside of the submarine are ballast tanks filled with water. Some of the water in the ballast tanks is then ejected, decreasing the density of the submarine. The free-body diagram in the figure shows the magnitude and direction of the forces acting on the submarine after the water is ejected. The acceleration of the submarine is most nearly
A \(0.10m/s^2\)
B \(0.11m/s^2\)
C \(0.40m/s^2\)
D \(1.1m/s^2\)
▶️Answer/Explanation
Ans:D
The acceleration is the net force divided by the object’s mass. The net force is the buoyancy force \((4.0×10^7)\) minus the weight of the object \(3.6×10^7\). This gives \(4×10^6N\) and, when divided by the mass of the object \((3.6×10^6)\), yields \(1.1m/s^2\)
Question
A sphere of mass 0.5kg is dropped into a column of oil. At the instant the sphere becomes completely submerged in the oil, the sphere is moving downward at 8m/s, the buoyancy force on the sphere is 4.0N, and the fluid frictional force is 4.0N . Which of the following describes the motion of the sphere at this instant?
A The sphere’s speed is decreasing while the sphere continues to move downward.
B The sphere is moving downward at a constant speed.
C The sphere’s speed is increasing while the sphere continues to move downward.
D The sphere’s speed is increasing as the sphere begins moving upward.
▶️Answer/Explanation
Ans:A
The net force acting on the sphere is 4.9N down from gravity, 4N up from the buoyant force, and 4N up from the frictional force. This results in a net force of 3.1N up and therefore a net acceleration upward. Since the sphere is moving downward, its speed will be decreasing.
Question
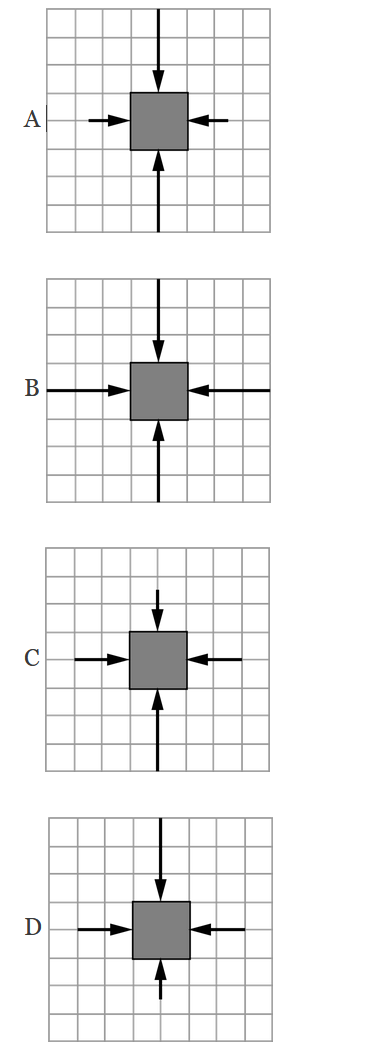
A solid cube is submerged in a container of water of density \(ρ_w\) . The cube has mass M , volume \(V_c\) , and density \(\frac{ρ_w}{2}\) . The water exerts an upward buoyant force on the cube of magnitude \(ρ_wV_cg\).
▶️Answer/Explanation
Ans:C
The pressure of the water increases with depth; thus, the force on the cube also increases with depth. The magnitude of the force exerted on the top face of the cube is less than that exerted on the bottom face. The average force exerted on each side of the cube has a magnitude between the forces exerted on the top and bottom.
Question
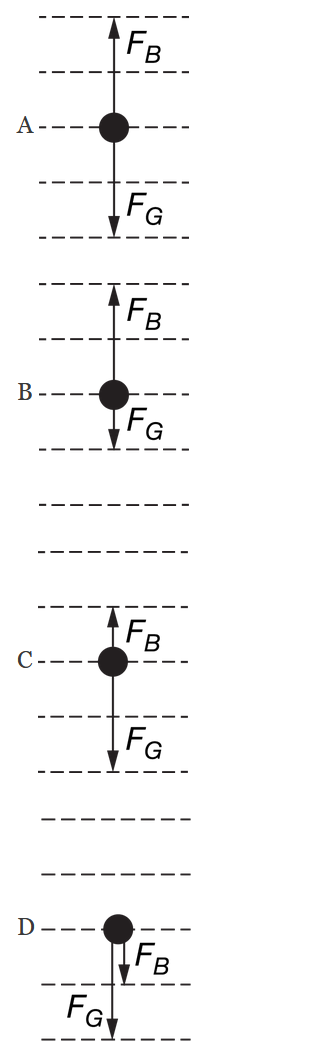
A sphere of metal is placed in a liquid. The sphere sinks with an acceleration less than g due to the vertical buoyant force \(F_B\) exerted by the liquid and the gravitational force \(F_g\) on the sphere. Which of the following best represents these two forces?
▶️Answer/Explanation
Ans:C
Since the sphere has a downward acceleration less than g , the buoyant force must be opposite the gravitational force, and downward force of gravity must be greater than the upward buoyant force.
Question
In the lab, a student is given a glass beaker filled with water with an ice cube of mass m and volume \(V_c\) floating in it.
The downward force of gravity on the ice cube has magnitude \(F_g\) . The student pushes down on the ice cube with a force of magnitude \(F_P\) so that the cube is totally submerged. The water then exerts an upward buoyant force on the ice cube of magnitude \(F_B\). Which of the following is an expression for the magnitude of the acceleration of the ice cube when it is released?
A \(\frac{F_B−F_g−F_P}{m}\)
B \(\frac{F_B−F_g}{m}\)
C \(\frac{F_P+F_g−F_B}{m}\)
D \(\frac{F_P−F_g}{m}\)
▶️Answer/Explanation
Ans:B
Once the cube is released, the only forces are the upward buoyant force and gravity downward. Since the object floated, the buoyant force is greater than gravity, so the latter should be subtracted from the former.