Question: (10 points, suggested time 20 minutes)
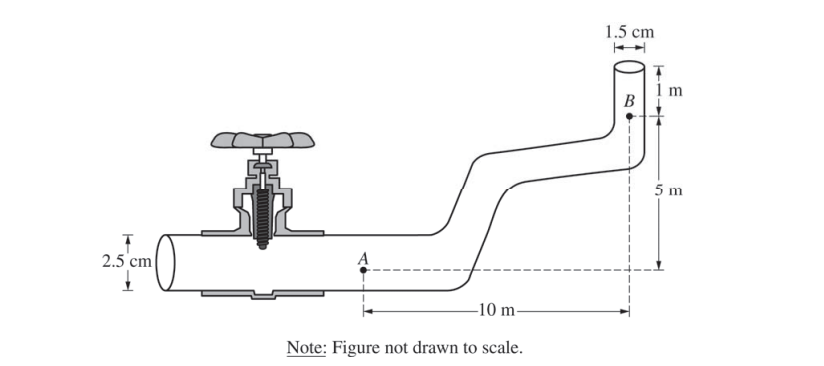
Two students observe water flowing from left to right through the section of pipe shown above, which decreases in diameter and increases in elevation. The pipe ends on the right, where the water exits vertically. At point A the water is known to have a speed of 0.50 m/s and a pressure of 2.0 × 105 Pa . The density of water is 1000 kg m3 .
(a) The students disagree about the water pressure and speed at point B. They make the following claims. Student Y claims that the pressure at point B is greater than that at point A because the water is moving faster at point B. Student Z claims the speed of the water is less at point B than that at point A because by conservation of energy, some of the water’s kinetic energy has been converted to potential energy of the Earth-water system.
i. Indicate any aspects of student Y’s claim that are correct.
ii. Indicate any aspects of student Y’s claim that are incorrect. Support your answer using appropriate physics principles.
iii. Indicate any aspects of student Z’s claim that are correct.
iv. Indicate any aspects of student Z’s claim that are incorrect. Support your answer using appropriate physics principles.
(b) Calculate the following at point B.
i. The speed of the water
ii. The pressure in the pipe
(c) A valve to the left of point A now closes off that end of the pipe. The section of pipe shown is still full of water, but the water is no longer flowing.
i. Calculate the absolute pressure at point A (the pressure that includes the effect of the atmosphere).
ii. An air bubble forms at point A. On the figure below, where the dot represents the air bubble, draw a free-body diagram showing and labeling the forces (not components) exerted on the bubble. Draw the relative lengths of all vectors to reflect the relative magnitudes of the forces.
▶️Answer/Explanation
Ans:
(a)
i.
The water is moving faster at point B
ii.
The pressure at point B is less than the pressure at point A because the water is moving faster and there is less water above point B. These principles can be qualified by Bemovlli’s equation
\(P_{A}+\rho gh_{A}+\frac{1}{2}\rho {V_{A}}^{2}= P_{B}+\rho ghB + \frac{1}{2}\rho {V_{B}}^{2}\)
iii.
Now of his claim is convert except that conservation of energy does occur.
iv.
The speed of the water at point B is greater than the speed at point A.
AAVA = ABVB
A larger area @ point A means a lower speed @ point A also, the kinetic energy isn’t transferred to potential energy. Rather, work is done on the system when the volume of the piye decreases, and both EK +Ug increase.
(b)
i.
AAVA =ABVB
(1.5625π) (.5) = (.562π)VB
VB = 1.39 m/s
ii.
PB = PA + ρghA + \(\frac{1}{2}\rho {V_{A}}^{2}- \rho gh_{B} – \frac{1}{2}\rho {V_{B}}^{2}\)
\(p_{b} = (2\not\equiv 5) + \frac{1}{2}(1000)(.25)-(1000)(10)(5)-\frac{1}{2}(1000)(1.39)^{2}\)
PB = 1.4 ∈ 5 Pa
(c)
i.
PA = P0 > ρgh
PA = 105 + (1000)(10)(6) = 160000 Pa
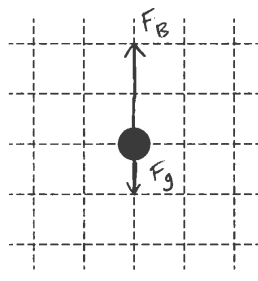
Since the density of air is less than H2O, the buoyant force is stronger than the gravitation force
Question: (10 points, suggested time 20 minutes)
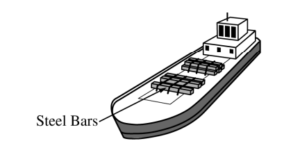
A large boat like the one shown above has a mass M b and can displace a maximum volume Vb . The boat is floating in a river with water of density Pwater and is being loaded with steel beams each of density Psteel and volume Vsteel . The boat owners want to be able to carry as many beams as possible.
(a) Derive an expression for the maximum number N of steel beams that can be loaded on the boat without exceeding the maximum displaced volume, in terms of the given quantities and physical constants, as appropriate.
(b) The captain realizes that oil is leaking from the boat, creating a thin film of oil on the water surface. In one area of the oil film the surface looks mostly green. Explain in detail how constructive interference contributes to the green appearance. Assume the index of refraction of the oil is greater than the index of refraction of the water.
(c) Later the boat is floating down the river with the water current, heading for a town. The river has a width of 60 m and a constant depth and flows at a speed of 5 km /hr. Partway to the town, the river narrows to a width of 30 m while its depth remains the same. Calculate the speed of the water in the narrow section.
▶️Answer/Explanation
Ans:
(a)
Fb = Fwater + Fsteel
Pwater Vb 9 = Mb9 + Psteel Vsteel N9
\(N = \frac{P_{water}V_{b}-M_{b}}{P_{steel}V_{steel}}\)
(b)
The oil floats on the water and because its index of retraction is great than air, light that refleets off of the oil is phase shifted by half a wave length. Some light travels into the ail and is refracted more downward due to higher area of refraction then air. This light reflects off of the bottom of the oil layer and is not phase shifted as the water has a higher index of refraction than the oil, the light then travels back up and reflects out of the oil at the some angle as the light was reflected off the top of the oil. The light reflected from both processes B constructive at the green wave length because the distance it look the light to travel considering its lessened wavelength through the oil phase shifted it half a green light wavelength to match the green light reflected off the oil.
(c)
d = depth (m)
V1 A1 = V2 A2
\(V_{2}=\frac{V_{1}A_{1}}{A_{2}} = \frac{(5)(d)(60)}{d(30)}= 10 km/hr\)
Question
A block of wood has a mass of 12 kg and dimensions 0.5 m by 0.2 m by 0.2 m.
(a) Find the density ρo of the wooden block.
(b) If the block is placed in water (ρ = 1000 kg/m3) with the square sides parallel to the water surface, how far beneath the surface of the water is the bottom of the block?
(c) A weight is placed on the top of the block. The block sinks to a point that the top of the block is exactly even with the water surface. Find the mass of the added weight.
▶️Answer/Explanation
Ans:
a) ρ = m/V = 12 / (0.5×0.2×0.2) = 600 kg / m3
b) The block will float based on its density. For floating, block weight = buoyant force.
mobjg = ph20 Vdisp g mobj = ph20 Asqaure(hsubmerged) 12 = 1000(0.2×0.2)hsub hsub = 0.3 m
c) The extra weight added should equal the extra buoyant force created by submerging the remaining 0.2 m of height.
Fb(extra) = ph20 Vdisp g = (1000)(0.2×0.2×0.2)(9.8) = 78.4 N 78.4 / 9.8 = 8kg of extra mass.
