Question: (10 points, suggested time 20 minutes)
A large boat like the one shown above has a mass M b and can displace a maximum volume Vb . The boat is floating in a river with water of density Pwater and is being loaded with steel beams each of density Psteel and volume Vsteel . The boat owners want to be able to carry as many beams as possible.
(a) Derive an expression for the maximum number N of steel beams that can be loaded on the boat without exceeding the maximum displaced volume, in terms of the given quantities and physical constants, as appropriate.
(b) The captain realizes that oil is leaking from the boat, creating a thin film of oil on the water surface. In one area of the oil film the surface looks mostly green. Explain in detail how constructive interference contributes to the green appearance. Assume the index of refraction of the oil is greater than the index of refraction of the water.
(c) Later the boat is floating down the river with the water current, heading for a town. The river has a width of 60 m and a constant depth and flows at a speed of 5 km /hr. Partway to the town, the river narrows to a width of 30 m while its depth remains the same. Calculate the speed of the water in the narrow section.
▶️Answer/Explanation
Ans:
(a)
Fb = Fwater + Fsteel
Pwater Vb 9 = Mb9 + Psteel Vsteel N9
\(N = \frac{P_{water}V_{b}-M_{b}}{P_{steel}V_{steel}}\)
(b)
The oil floats on the water and because its index of retraction is great than air, light that refleets off of the oil is phase shifted by half a wave length. Some light travels into the ail and is refracted more downward due to higher area of refraction then air. This light reflects off of the bottom of the oil layer and is not phase shifted as the water has a higher index of refraction than the oil, the light then travels back up and reflects out of the oil at the some angle as the light was reflected off the top of the oil. The light reflected from both processes B constructive at the green wave length because the distance it look the light to travel considering its lessened wavelength through the oil phase shifted it half a green light wavelength to match the green light reflected off the oil.
(c)
d = depth (m)
V1 A1 = V2 A2
\(V_{2}=\frac{V_{1}A_{1}}{A_{2}} = \frac{(5)(d)(60)}{d(30)}= 10 km/hr\)
Question: (10 points, suggested time 20 minutes)
A student notices many air bubbles rising through the water in a large fish tank at an aquarium.
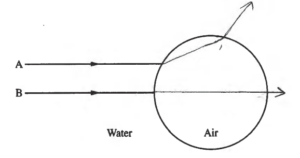
(a) In the figure below, the circle represents one such air bubble, and two incoming rays of light, A and B, are shown. Ray B points toward the center of the circle. On the diagram, draw the paths of rays A and B as they go through the bubble and back into the water. Your diagram should clearly show what happens to the rays at each interface.
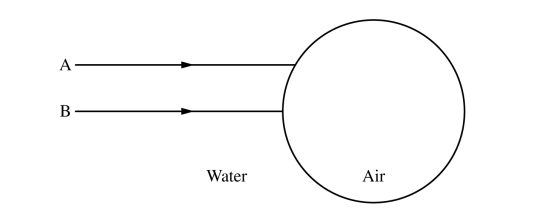
(b) The bubble has a volume V1 , the air inside it has density PA , and the water around it has density PW . The bubble starts at rest and has a speed vf when it has risen a height h. Assume that the change in the bubble’s volume is negligible. Derive an expression for the mechanical energy dissipated by drag forces as the bubble rises this distance. Express your answer in terms of the given quantities and fundamental constants, as appropriate.
(c) At a particular instant, one bubble is 4.5 m below the water’s surface. The surface of the water is at sea level, and the density of the water is 1000 kg m3 .
i. Determine the absolute pressure in the bubble at this location.
ii. The bubble has a volume V1 when it is 4.5 m below the water’s surface. Assume that the temperature of the air in the bubble remains constant as it rises. In terms of V1 , calculate the volume of the bubble when it is just below the surface of the water.
iii. If the air in the bubble cooled as it rose, the volume of the bubble would be less than the value calculated in part (c)(ii). Use physics principles to briefly explain why.
▶️Answer/Explanation
Ans:
(a)
(b)
buoyant force = pwV1.9
gravitational force = PA V1.9
Net upward force = V19 (PW-PA)
work done by net force = change in KE + change in PE + energy lost to drag
W = Fd ⇒ V19 (PW-PA) . h = \(\frac{1}{z}\) PAV1.Vfz + PAV1.g.h+ energy
lost to drag
(c)
i.
Pabs = pgh + Patm
Pabs = 1000.9.8.4.5 + 1.105 Pa
=1.4.105Pa
ii.
PV = nRT ⇒ P1V1 = P2V2 (constant modes and temperature)
1.4.105.V1 = 1.105.V2 V2 = 1.4V1
iii.
PV = nRT ⇒ \(\frac{P_{1}V_{1}}{T_{1}}=\frac{P_{2}V_{2}}{T_{2}}\) if temperature varies
if T2 < T1, and the ratio of \(\frac{P_{1}}{P_{2}}\) is the same, V2 must be less than V1
For the expression to stay true.
Question
A group of students have been asked to determine the spring constant k of the following setup. They have a known mass and a very smooth tabletop. The only additional equipment they have is metersticks and rulers.
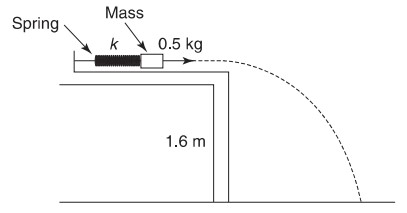
(a) Describe an experimental procedure to determine the spring constant k . You may wish to label the diagram above further to help in your description. Indicate what measurements you would take and how you would take them. Include enough detail so that another student could carry out your procedure.
(b) What are the expected results of the experiment? Determine your independent and dependent variables. Sketch out the expected graph. Derive the relationship you would expect to find.
(c) What common sources of error in your procedure might happen during this investigation? What steps could you take to minimize these errors?
(d) A group of students collected the following data; x is for the spring and D is along the ground. The students found a discontinuity in the behavior of the graph. Graph the data and determine a value for k . Offer a possible explanation for the discontinuity.
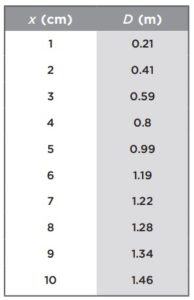

▶️Answer/Explanation
Ans:
(a) For various measured compressions of the spring (x), measure horizontal range for the mass (R). Range should be measured along the floor from beneath the edge of the table to where the mass first hits the ground. Multiple trials for each compression x should be taken so that the average range of values can be determined.
(b) The independent variable is the one the experimenter controls and manipulates directly. In this case, the independent variable is the compression x . The dependent variable is the one measured as a result of changes in the independent variable. In this case, the dependent variable is the range. Independent variables are graphed on the horizontal axis. Theoretical prediction:
\(\frac{1}{2}kx^{2}=\frac{1}{2}mv^{2}\)
\(v=(k/m)^{1/2}x\)
This velocity is the horizontal projectile’s velocity. The time in flight is found from the height of the table:
\(H=\frac{1}{2}gt^{2}\)
\(1.6m=4.9t^{2}\)
\(t = 0.57s\)
\(R=vt=(k/m)^{1/2}xt=.57(k/m)^{1/2}x\)
Using the fixed values for m and t: \(R=0.806k^{1/2}x\)
(c) The major source of error is friction of the tabletop between the end of the spring and the edge of the table. Ensuring that this distance is small and that the surfaces involved are smooth will minimize this error.
(d) 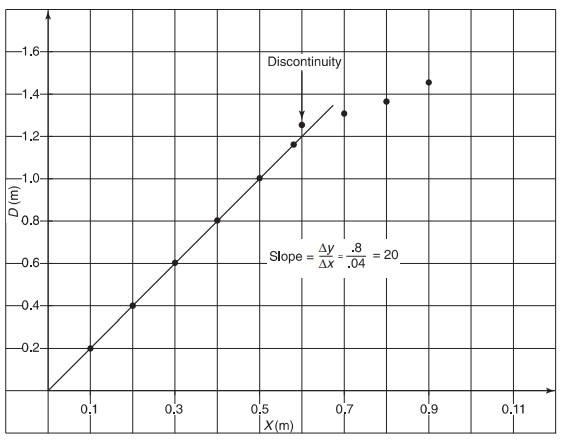
The discontinuity is probably caused by exceeding the limit of elasticity for this spring. Hooke’s law assumes that the material is perfectly elastic and resumes its shape after being stretched or compressed:
Slope = 20 = 0.806 \(k^{1/2}\) (from part (b))
Solving for k: \(k\) = 616 N/m
