Question: (10 points, suggested time 20 minutes)
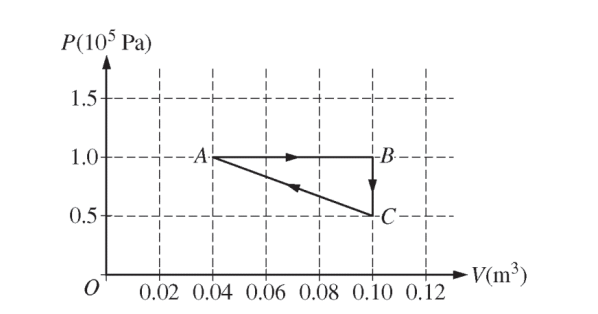
Two moles of a monatomic ideal gas are enclosed in a cylinder by a movable piston. The gas is taken through the thermodynamic cycle shown in the figure above. The piston has a cross-sectional area of 5 × 10-3 m2 .
(a)
i. Calculate the force that the gas exerts on the piston in state A, and explain how the collisions of the gas atoms with the piston allow the gas to exert a force on the piston.
ii. Calculate the temperature of the gas in state B, and indicate the microscopic property of the gas that is characterized by the temperature.
(b)
i. Predict qualitatively how the internal energy of the gas changes as it is taken from state A to state B. Justify your prediction.
ii. Calculate the energy added to the gas by heating as it is taken from state A to state C along the path ABC.
(c) Determine the change in the total kinetic energy of the gas atoms as the gas is taken directly from state C to state A.
▶️Answer/Explanation
Ans:
\(P = \frac{F}{A}\) FA = PA = 1 × 105 Pa × 5 × 10-3 m2
FA = 500 N
The collision of the gas atoms with the piston allow the gas to exeit a force or the piston because the molecules are in rapid, random motion, and ave frequently colliding with the walls of the cylinder and the piston. When molecules hit the piston in rapid random motion, a force is exerted.
PV = nRT T= \(\frac{PV}{nR}\) = \(\frac{1.0\times 10^{5}Pa \times 0.10m^{3}}{2nd\times 8.31\frac{J}{Molk}}\)
T = 602 K
The average kinetic energy of the molecules of gas is characterized by the temperature, and average kinetic energy relates to the microscopic property of the speed of the gas molecules.
(b)
i.
The internal energy of the gas increases as it is taken from state A to state B because the pressure remains constant and volume increases, meaning that temperature increases. When temp increases, internal energy increases because \(U = \frac{3}{2}nRT.\)
ii.
ΔV = Q + W \(\Delta V = \frac{3}{2}nR\Delta T\) \(\Delta T = \frac{P_{C}V_{C}-P_{A}V_{A}}{nR}\)
1496J = -6000 J + Q ΔV = 1, 496 J ΔV = 60 K
W = P Δ V
W = 1×105Pa×0.06 m3
W = -6000 J
ii.
Δ V = \(\frac{3}{2}nR\Delta T\) Δ T = TC – TA = \(\frac{P_{A}V_{A}}{nR}-\frac{P_{C}V_{C}}{nR}\)
Δ V = \(\frac{3}{2}.2nd 8.31\frac{J}{molk}. 60K\)
Δ T = \(\frac{0.5\times 10^{5}Pa\times 0.10m^{3}}{2nd \times 8.31\frac{J}{molk}}-\frac{1.0\times 10^{5}Pa\times 0.04m^{3}}{2nd \times 8.31\frac{J}{molk}}\)
Δ V = 1496 J Δ T = -60 K
