Question: (10 points, suggested time 20 minutes)
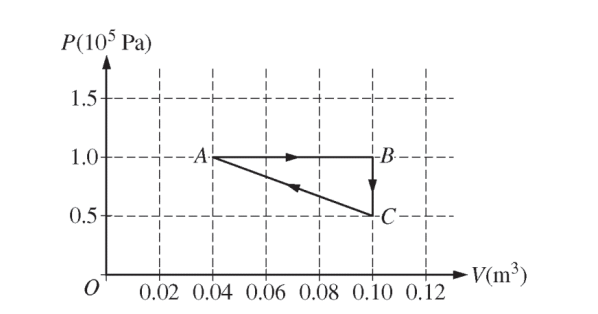
Two moles of a monatomic ideal gas are enclosed in a cylinder by a movable piston. The gas is taken through the thermodynamic cycle shown in the figure above. The piston has a cross-sectional area of 5 × 10-3 m2 .
(a)
i. Calculate the force that the gas exerts on the piston in state A, and explain how the collisions of the gas atoms with the piston allow the gas to exert a force on the piston.
ii. Calculate the temperature of the gas in state B, and indicate the microscopic property of the gas that is characterized by the temperature.
(b)
i. Predict qualitatively how the internal energy of the gas changes as it is taken from state A to state B. Justify your prediction.
ii. Calculate the energy added to the gas by heating as it is taken from state A to state C along the path ABC.
(c) Determine the change in the total kinetic energy of the gas atoms as the gas is taken directly from state C to state A.
▶️Answer/Explanation
Ans:
\(P = \frac{F}{A}\) FA = PA = 1 × 105 Pa × 5 × 10-3 m2
FA = 500 N
The collision of the gas atoms with the piston allow the gas to exeit a force or the piston because the molecules are in rapid, random motion, and ave frequently colliding with the walls of the cylinder and the piston. When molecules hit the piston in rapid random motion, a force is exerted.
PV = nRT T= \(\frac{PV}{nR}\) = \(\frac{1.0\times 10^{5}Pa \times 0.10m^{3}}{2nd\times 8.31\frac{J}{Molk}}\)
T = 602 K
The average kinetic energy of the molecules of gas is characterized by the temperature, and average kinetic energy relates to the microscopic property of the speed of the gas molecules.
(b)
i.
The internal energy of the gas increases as it is taken from state A to state B because the pressure remains constant and volume increases, meaning that temperature increases. When temp increases, internal energy increases because \(U = \frac{3}{2}nRT.\)
ii.
ΔV = Q + W \(\Delta V = \frac{3}{2}nR\Delta T\) \(\Delta T = \frac{P_{C}V_{C}-P_{A}V_{A}}{nR}\)
1496J = -6000 J + Q ΔV = 1, 496 J ΔV = 60 K
W = P Δ V
W = 1×105Pa×0.06 m3
W = -6000 J
ii.
Δ V = \(\frac{3}{2}nR\Delta T\) Δ T = TC – TA = \(\frac{P_{A}V_{A}}{nR}-\frac{P_{C}V_{C}}{nR}\)
Δ V = \(\frac{3}{2}.2nd 8.31\frac{J}{molk}. 60K\)
Δ T = \(\frac{0.5\times 10^{5}Pa\times 0.10m^{3}}{2nd \times 8.31\frac{J}{molk}}-\frac{1.0\times 10^{5}Pa\times 0.04m^{3}}{2nd \times 8.31\frac{J}{molk}}\)
Δ V = 1496 J Δ T = -60 K
Question: (10 points, suggested time 20 minutes)
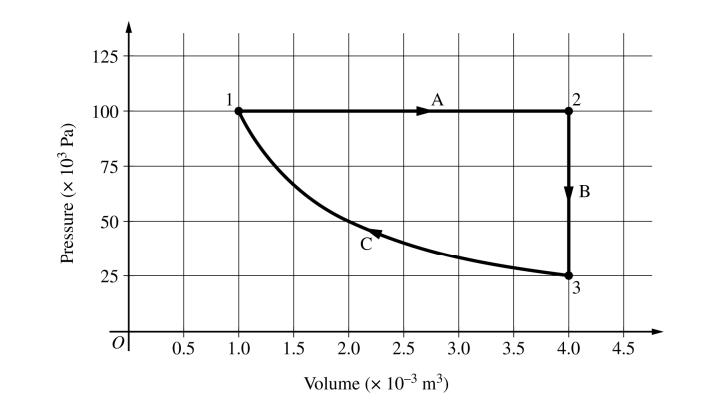
A sample of ideal gas is taken through the thermodynamic cycle shown above. Process C is isothermal.
(a) Consider the portion of the cycle that takes the gas from state 1 to state 3 by processes A and B. Calculate the magnitude of the following and indicate the sign of any nonzero quantities.
- The net change in internal energy ΔU of the gas
- The net work W done on the gas
- The net energy Q transferred to the gas by heating
(b) Consider isothermal process C.
i. Compare the magnitude and sign of the work W done on the gas in process C to the magnitude and sign of the work in the portion of the cycle in part (a). Support your answer using features of the graph.
ii. Explain how the microscopic behavior of the gas particles and changes in the size of the container affect interactions on the microscopic level and produce the observed pressure difference between the beginning and end of process C.

(c) Consider two samples of the gas, each with the same number of gas particles. Sample 2 is in state 2 shown in the graph, and sample 3 is in state 3 shown in the graph. The samples are put into thermal contact, as shown above. Indicate the direction, if any, of energy transfer between the samples. Support your answer using macroscopic thermodynamic principles.
▶️Answer/Explanation
Ans:
(a)
W = -PΔV
W = -100.103Pa• (4.10-3 m3-1.10-3m3 )
W = -300J
ΔU = Q+W
o = Q-300J
Q = 300J
ΔU = 100.103Pa•1.103m3-25.103Pa•4.10-3m3
(b) i.
Work can be measured by the area under the process. Because process A has a greater average pressure than process C, the work done on the gas through process A is greater than that of process C. No work occurs during process process B. Process A increases in volume, so negative work is done on the gas. Process C decreases the volume, so position work is done.
ii.
As the volume decreases, gas particles more closer together, so they collide more frequently with each other and with the walls of the container.
(c) Because PV = nRT, P2 > P3, V2 = V3, and n3 = n2, T2>T3, meaning sample 2 has a higher temperature than sample 3. Energy will flow from high temperature to low temperature so than sample 2 to sample 3.
Question
An ideal gas initially has pressure po, volume Vo, and absolute temperature To. It then undergoes the following series of processes:
I. It is heated, at constant volume, until it reaches a pressure 2po.
II. It is heated, at constant pressure, until it reaches a volume 3 Vo.
III. It is cooled, at constant volume, until it reaches a pressure po.
IV. It is cooled, at constant pressure, until it reaches a volume Vo.
a. On the axes below
i. draw the p-V diagram representing the series of processes;
ii. label each end point with the appropriate value of absolute temperature in terms of To.
b. For this series of processes, determine the following in terms of po and Vo.
i. The net work done on the gas
ii. The net change in internal energy
iii. The net heat absorbed
c. Determine the heat transferred during process 2 in terms of po and Vo.
▶️Answer/Explanation
Ans:
a. 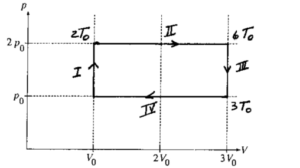
b. i. The work done on the gas is the area enclosed. Area = width × height = 2V0 × P0 = –2P0V0 (negative since it is a clockwise cycle)
ii. ΔU = 0 for any cycle
iii. since ΔU = 0, Q = –W = +2P0V0
c. For process 2, W = –PΔV = –2P0 × (3V0 – V0) = –4P0V0
and ΔU = 3/2 nRΔT = 3/2 nR(6T0 – 2T0) = +6 nRT0 = +6P0V0
Q = ΔU – W = +6 P0V0 – (–4P0V0) = +10P0V0
