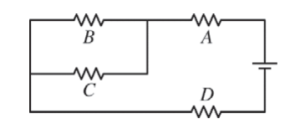
Question: (7 points, suggested time 13 minutes)
A circuit contains a battery and four identical resistors arranged as shown in the diagram above.
(a) Rank the magnitude of the potential difference across each resistor from greatest to least. If any resistors have potential differences with the same magnitude, state that explicitly. Briefly explain your reasoning.
Ranking:
Brief explanation:
Resistor B is now removed from the circuit, and there is no connection between the wires that were attached to it. The new circuit diagram is shown below.
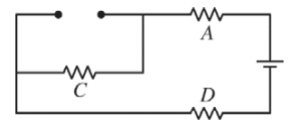
(b) When resistor B is removed, does the current through resistor A increase, decrease, or remain the same?
________Increase __________Decrease ___________Remain the same
Briefly explain your reasoning.
(c) When resistor B is removed, does the current through resistor C increase, decrease, or remain the same?
_________ Increase ________ Decrease ___________ Remain the same
Briefly explain your reasoning.
▶️Answer/Explanation
Ans:
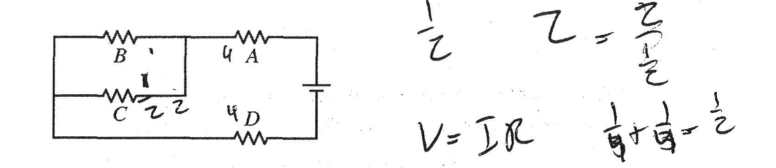
(a)
A has same potential difference as D. B \(\frac{1}{3}\) , C are less than A \(\frac{1}{3}\) , D but equal to each other.
Brief explanation:
Since A and D are identical resists with the same amount of current through both of them, they have the same potential difference (V – IR) B and C are in a parallel structure so current gets split between them, making each of their potential differences v = \(\frac{1}{z}\) IR
(b)
X Decrease
Current (I) is \(\frac{potential difference}{resistance}\) (I = \(\frac{V}{R}\) )
When B and C where in a parallel circuit, B \(\frac{1}{3}\) C’s combined resistance were less than either one of them. Therefore, is A, C, and D are all in a series there will be more resistance which equals less current.
(c)
X Increase
When B \(\frac{1}{3}\), C where in a parallel circuit, current was split evenly between them. Current is the same for all resisters in a serves, and since the removal of be creates a series circuit including C, C will get all of the current within the circuit.
Question: (7 points, suggested time 13 minutes)
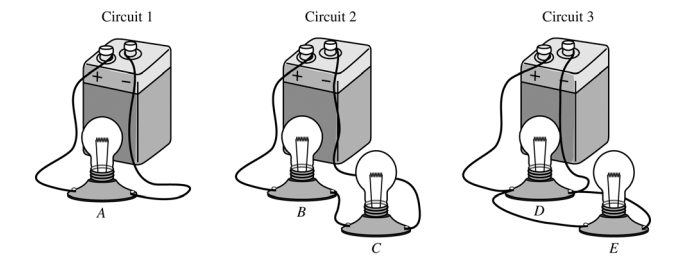
In the three circuits shown above, the batteries are all identical, and the lightbulbs are all identical. In circuit 1 a single lightbulb is connected to the battery. In circuits 2 and 3, two lightbulbs are connected to the battery in different ways, as shown. The lightbulbs are labeled A–E.
(a) Rank the magnitudes of the potential differences across lightbulbs A, B, C, D, and E from largest to smallest.
If any lightbulbs have the same potential difference across them, state that explicitly.
Ranking:
Briefly explain how you determined your ranking.
(b) The batteries all start with an identical amount of usable energy and are all connected to the lightbulbs in the circuits at the same time.
In which circuit will the battery run out of usable energy first?
____ Circuit 1 ____ Circuit 2 ____ Circuit 3
In which circuit will the battery run out of usable energy last?
____ Circuit 1 ____ Circuit 2 ____ Circuit 3
In a clear, coherent paragraph-length response that may also contain equations and drawings, explain your reasoning.
▶️Answer/Explanation
Ans:
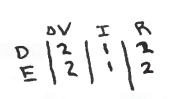
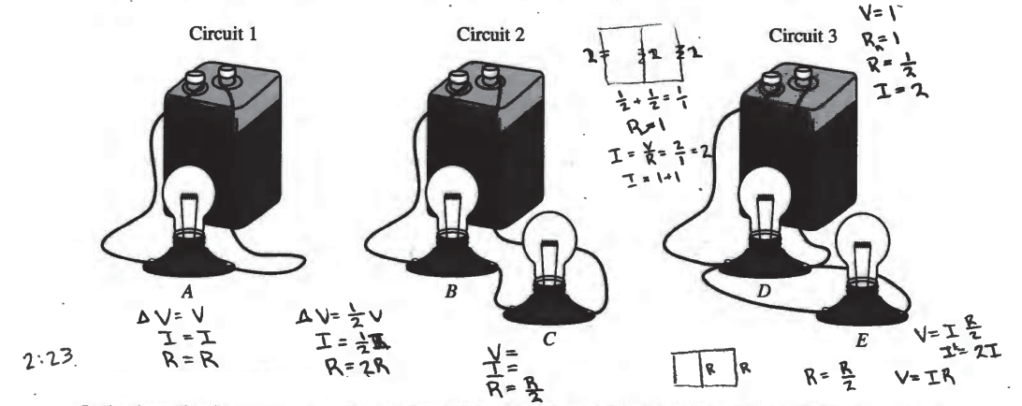
(a)
Δ V : ( A = D = E) > (B = C)
A, D, B E all have the potential difference equal to the voltage of the battery because all have direct pathways to the battery. Bulbs B & C share access to the same battery; thus, the potential difference across them is just half that of Bulbs A, D, B E.
(b)
√ Circuit 3
√ Circuit 2
As a true parallel circuit, the battery in circuit 3 will run out of power the soonest because it is feeding enough power to power 2 bulbs at full strength. Mathematically speaking, since \(\frac{1}{R_{P}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + ……,\) a parallel circuit has 1/n the resistance of a single bulb circuit. Therefore, the current, I, is n times that of a single bulb circuit. In this case, n = 2, so the battery has twice the current running through it that the battery in circuit A would have. This increased current means that the battery runs out of energy faster. On the other hand, circuit 2 retains energy the longest because its resistance is higher than a single bulb circuit. Rseries = R1 + R2 + …., so Rseries = nR. Since \(I = \frac{V}{R}\), greater resistance values for equal voltage batteries produces less current. This lower current carries energy from the battery at a slower pace; thus, the battery, retains energy is keeps the lighbulbs lit longer than a single-bulb circuit.
Question
You are given three 2-ohm resistors, some wire, a variable DC voltage supply, a voltmeter, and an ammeter.
(a) Draw a schematic diagram of a circuit that will produce an equivalent resistance of 3 ohms as well as measure the circuit current and source voltage.
(b) Which, if any, of these components are assumed to have zero internal resistance? Which, if any, of these components are assumed to have infinite resistance? Justif your choices.
(c) Trace out one complete loop in your circuit, and prove Kirchoff’s loop rule. Once you set up your rule, assume a setting of 6 volts on the power supply. Verify your rule numerically.
(d) A student wishes to measure the voltage and current in a simple circuit using small lightbulbs instead of commercially manufactured resistors.She finds that after a short while, the current in the ammeter is decreasing. How might she account for this?
▶️Answer/Explanation
(a)
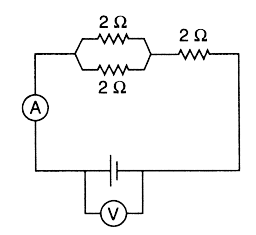
(b) Ammeters, wires, and power supplies are assumed to have zero internal resistance as they have no resistance indicated in the circuit diagram. If there were any resistance, unaccounted losses of voltage would occur in our circuit. When modeling actual resistance inside of components, an “internal” resistor is added to the circuit diagram. Voltmeters would create a parallel path if they did not have infinite resistance. To the extent they have less than infinite resistance, the addition of voltmeters to the circuit would effectively lower the resistance, thereby lowering the voltage reading.
(c) Kirchhoff’s loop rule states that the sum of voltages changing around the loop must be zero. As an example of this, start to the right of the power supply and trace a loop clockwise through the top parallel resistor and then the resistor to the right and back to our starting point. Tracing our changes in voltage:
+ V − ( I /2) R − IR = 0
For the entire circuit:
V = IR
6 = I (3)
I = 2 amps
Loop rule:
+6 − (1)(2) − (2)(2) = 6 − 2 − 4 = 0
(d) The lightbulbs get hot very quickly, which increases their electrical resistance. This, in turn, reduces the current measured by the ammeter.