Question: (10 points – suggested time 20 minutes)
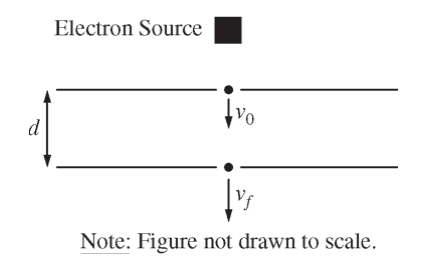
The apparatus shown in the figure above consists of two oppositely charged parallel conducting plates, each with area A = 0.25 m2 , separated by a distance d = 0.010 m . Each plate has a hole at its center through which electrons can pass. High velocity electrons produced by an electron source enter the top plate with speed v0 = 5.40 ×106 m/s, take 1.49 ns to travel between the plates, and leave the bottom plate with speed vf = 8.02 ×106 m/s .
(a) Which of the plates, top or bottom, is negatively charged? Support your answer with a reference to the direction of the electric field between the plates.
(b) Calculate the magnitude of the electric field between the plates.
(c) Calculate the magnitude of the charge on each plate.
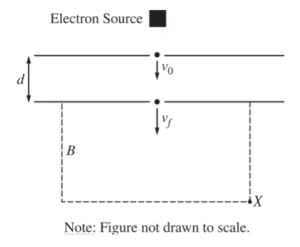
(d) The electrons leave the bottom plate and enter the region inside the dashed box shown below, which contains a uniform magnetic field of magnitude B that is perpendicular to the page. The electrons then leave the magnetic field at point X.
i. On the figure above, sketch the path of the electrons from the bottom plate to point X. Explain why the path has the shape that you sketched.
ii. Indicate whether the magnetic field is directed into the page or out of the page. Briefly explain your choice.
▶️Answer/Explanation
Ans:
The top plate is negatively charged. The electrons increase their speed, s their acceleration is downward. This means by F = ma, the electric force points downward. Since these are electrons, the force is in the opposite direction of the field lines, which thus point up. Field lines point towards the negative plate, which is the top one
W = ΔKE
Vg = ΔKE
Ed = \(\frac{\Delta KE}{g}\)
\(E = \frac{1}{2}\left ( \frac{1}{q} \Delta KE\right )\)
\(E = \left ( \frac{1}{0.010m} \right )\left ( \frac{1}{1.6\times 10^{-19}C} \right )\left ( \frac{1}{2} \right )\left ( 9.11\times 10^{-31}Kg \right )\left ( (8.02\times 10^{6}m/s)^{2}-(5.40\times 10^{6}m/s)^{2} \right )=1.0\times 10^{4}N/C\)
(c)
\(C = \frac{\varepsilon .A}{d}\)
\(\frac{Q}{V} = \frac{\varepsilon .A}{d}\)
\(Q = \frac{\varepsilon 0EdA}{d} = \varepsilon 0EA\)
= (8.85 × 10-12 C2/Nm2) (1.0×104N/C) (0.25m2) = 2.2×10-8C
(d)
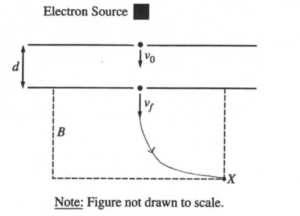
i.
The magnetic force is always perpendicular to the direction of velocity. Thus, the force acts as a centripetal force, so the electrons undergo circular motion.
ii.
The magnetic field is directed out of the page. By the right hand rule (force to the right, velocity down,) the magnetic field is into the page. Since the electrons are negatively charged, we switch the direction so the field is out of the page (the right hand rule applies to positively charged particles.)
Question
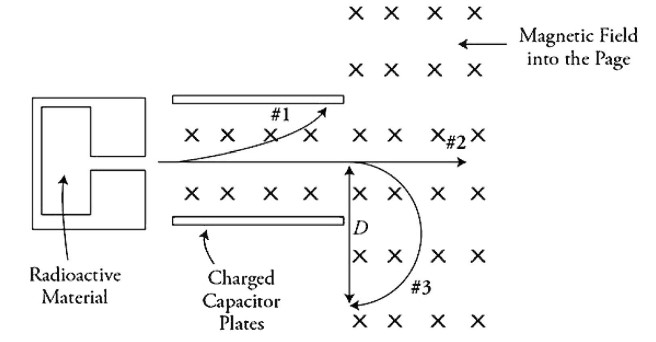
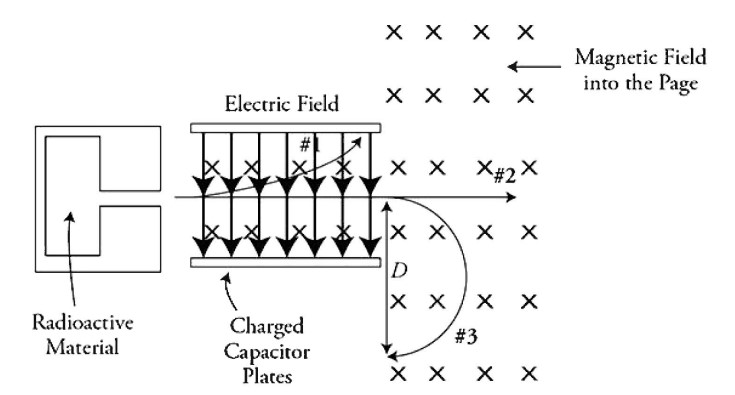
A sample of radioactive sources is enclosed within a lead-shielded container with a narrow exit aperture that ensures that any ejected particles will exit the container directly to the right. The ejected particles pass between charged parallel conductive plates and a region of magnetic field that is directed into the page. Three particles exit the container and follow paths as shown in the figure. Students observing the particles make these statements:
Student A: Both particles 2 and 3 pass through the capacitor region undeflected so there is no net force on them. They both must be neutral particles.
Student B: The path of particle 3 implies it has a negative charge. Therefore, the bottom plate of the capacitor must be negatively charged.
Student C: Particle 1 is positive because it curves upward.
(A) List all parts of the students’ statements that are correct. Explain your reasoning for each.
(B) List all parts of the students’ statements that are incorrect. Explain your reasoning for each.
( C) On the figure, sketch the electric field vectors between the capacitor plates that are consistent with the motion of the particles.
(D) Particle 3 is detected at distance D from its exit point from the capacitor plates. Using this information, derive an expression for the charge to mass ratio (q/m) of particle 3 in terms of D, E (the electric field between the capacitor plates), and B (the magnetic field).
(E) Using the equation derived in (D), a charge to mass ratio (q/m) of 1.76 x \(10^{11}\) C/kg was calculated. Explain how this number could be used to determine the set of possible masses of particle 3.
(F) One of the radioactive sources enclosed in the shielded container is fermium-257, which has 100 protons and a half-life of 100.5 days. Fermium transmutes into Californium (Cf) by emitting an alpha particle with a velocity of 2.0 x \(10^{7}\) m/s.
(i) Write the complete nuclear equation of this decay reaction.
(ii) Write, but do not solve, a symbolic expression that could be used to calculate the mass released to energy in one single fermium-257 decay.
(iii) Assuming the fermium-257 is isolated and stationary, calculate the velocity of the Californium nucleus after the alpha particle is ejected.
▶️Answer/Explanation
Ans:
Part (A)
Student A is correct that particles 2 and 3 have no net force acting on them while between the charged plates. This is evident in the fact that they travel in a straight line through the charged plate.
AND
Student A is correct in stating that particle 2 is neutral as it travels in a straight line through the magnetic field. Knowing that a charged particle will experience a force while passing through a magnetic field, particle 2 must be uncharged.
Student B is correct in stating that particle 3 must have a charge, since a moving charged particle will experience a force when passing through a magnetic field. Student B is also correct in stating that the path implies a negative charge. According to the right-hand rule for a charged particle in a magnetic field, the direction of force on a moving charged particle will be perpendicular to both the magnetic field and the direction of positive charge motion. Using this right-hand rule, we find a circular path directed upward for a positive charge, thus the downward curve of particle 3 suggests a negative charge.
AND
Student B is correct in stating that the bottom plate must be negatively charged. Since particle 3 is negative as previously stated, the negative charge will experience a downward force from the magnetic field. In order to maintain a straight line and thus no acceleration, particle 3 must experience an upward force to balance the downward force. This can be achieved only if the bottom plate repels the negative charge upward, indicating that the bottom plate is negatively charged.
Part (B)
Student A is incorrect in stating that particle 3 is neutral as evidenced by the fact that it experiences a force exerted by the magnetic field and arcs downward as soon as it leaves the electric field between the charged plates.
Student C is incorrect in stating that particle 1 is positively charged. Although the direction of the magnetic force on a positive charge would be upward, the bottom plate is negative and the top plate is positive. Thus, the electric force on particle 1 is downward. It is not possible to tell from the given information what the charge of particle 1 is. We can only say for sure that particle 1 has a net charge.
Part (C)
Part (D)
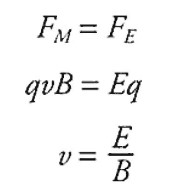
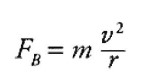
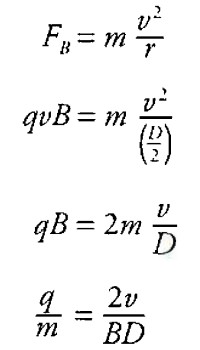
Substituting in the equation for velocity from above: 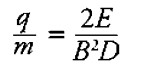
Part (E)
Example: The mass can be found by dividing the charge by the charge to mass ratio (q/m). However, we know that particles come only in multiples of the electron charge. So, dividing the multiple of the electron charge by the charge to mass ratio will give us a set of possible masses for particle 3.
Part (F)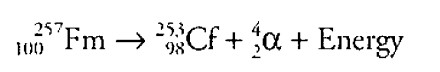
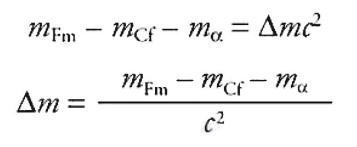
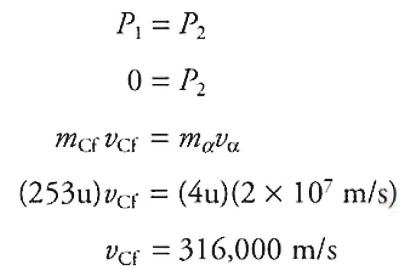
Question

A scientist constructs a device shown in the figure. Region I consists of a charged parallel plate capacitor with vertical plates separated by a distance x. The left plate has a small opening that accelerated particles can pass through. Region II has two large horizontal capacitor plates with a separation of y and a magnetic field created by current-carrying solenoid coils, which are not pictured in the figure. The magnetic field is directed upward out of the page. In an experiment a single proton P is placed at the launch point near the right plate in Region I. The proton accelerates to the left through the hole and continues on a straight path through Region II as seen in the figure.
(A) What is the direction of the electric field in Region I? Justify your answer.
(B) Which capacitor plate has the higher potential in Region II? Justify your answer.
(C) The experiment is repeated, replacing the proton with an alpha particle that has a mass approximately four times larger than the proton and a charge two times larger than the proton. The alpha particle is released from the launch point and passes through the hole in the left plate. Compare the motion of the alpha particle to the motion of the proton through Regions I and II. Justify your reason mg. The Region I capacitor plates have a potential difference of 5400 V and a plate separation x of 0.14 m. The Region II capacitor plates have a separation y of 0.060 m and a magnetic field of 0.50 T.
(D) A proton is again placed at the launch point near the right plate in Region I. Derive an algebraic expression for the velocity of the proton as it passes through the hole in the left plate. Use your expression to calculate the numerical value of the velocity.
(E) Using your work from (D), derive an algebraic expression for the potential difference that must be applied to the capacitor in Region II so that the proton 1noves in a straight line through the region. Use your expression to calculate the numerical value of the potential difference.
(F) Keeping the potential difference the same as the calculated value from (E), the scientist places an unknown particle at the launch point and observes that it travels straight through both Regions I and II just as the proton did. Discuss what the scientist can deduce about the unknown particle. Justify your answer, making appropriate reference to the algebraic expressions derived in (D) and (E).
▶️Answer/Explanation
Ans:
Part (A)
Electric field is to the left. The electric field points in the direction of force on a positive charge. The proton accelerates to the left; therefore, the force is to the left and the electric field is also to the left.
Part (B)
The upper plate must have a higher potential. Utilizing the right-hand rule for forces on moving positive charges, and showing that the proton receives a magnetic force upward from the magnetic field. The electric force is equal and opposite in direction to the magnetic force so that the proton will travel in a straight line. Electric fields point from higher potential to lower potential. Thus, the upper plate is a higher potential.
Part (C)
The alpha particle will curve downward in Region II. The alpha particle will exit Region I with a slower velocity. The electric potential energy has doubled, but the mass has quadrupled leading to a smaller exit velocity. (Or, in Region I the electric force on the charge has doubled, but the mass has quadrupled, leading to a smaller acceleration and exit velocity.) The electric force will now be larger than the magnetic force causing the alpha particle to arc downward. The electric force will double as the change doubles: \(B_{E}=q_{E}\). The magnetic force will not increase as much as the electric force. Even though the charge doubles, the velocity is now slower: \(P_{M}=qvB\).
Part (D)
Conservation of energy: \(AR_{E}=K\)
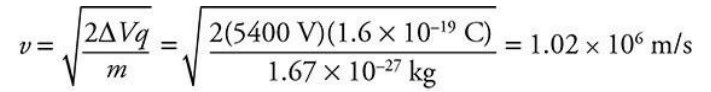
Part (E)
To move in a straight line: \(B_{E}=P_{M}\)
Magnetic force equal to electric force: Eq=qvB
\(E=\frac{\Delta V}{y}=vB\)
Equations with substitutions:
AK= yvB — (0.060)(1.02 x \(10^{6}\) m/s)(0.50 T)
AK= 30,600 V
Part (F)
From the equation derived in (E) AK= yvB, we know that the velocity of the particle is the same because AK, y, and B are all the same.
From the equation in (D) \(v=\sqrt{\frac{2\Delta Vq}{m}}\), we know that both v and AT are the same. Thus, we can deduce the charge to mass ratio q/m of the unknown particle.
