Question: (7 points, suggested time 13 minutes)
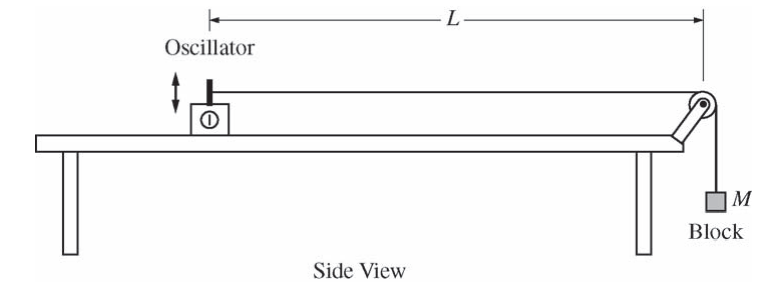
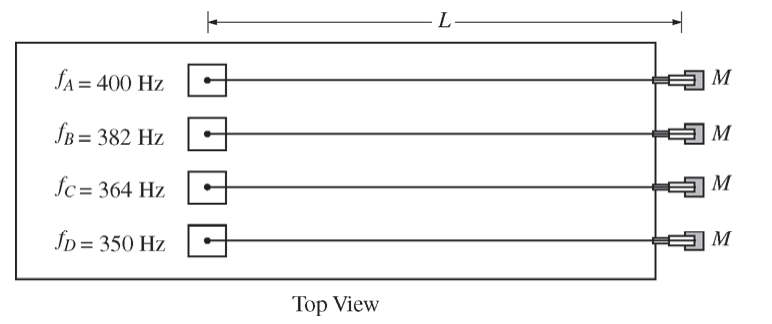
The figure above shows a string with one end attached to an oscillator and the other end attached to a block. The string passes over a massless pulley that turns with negligible friction. Four such strings, A, B, C, and D, are set up side by side, as shown in the diagram below. Each oscillator is adjusted to vibrate the string at its fundamental frequency f. The distance between each oscillator and pulley L is the same, and the mass M of each block is the same. However, the fundamental frequency of each string is different.
The equation for the velocity v of a wave on a string is \(v = \sqrt{\frac{F_{T}}{m/L}},\) where FT is the tension of the string and m/L is the mass per unit length (linear mass density) of the string.
(a) What is different about the four strings shown above that would result in their having different fundamental frequencies? Explain how you arrived at your answer.
(b) A student graphs frequency as a function of the inverse of the linear mass density. Will the graph be linear? Explain how you arrived at your answer.
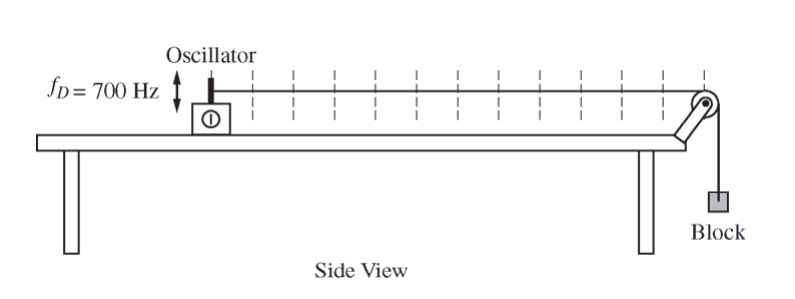
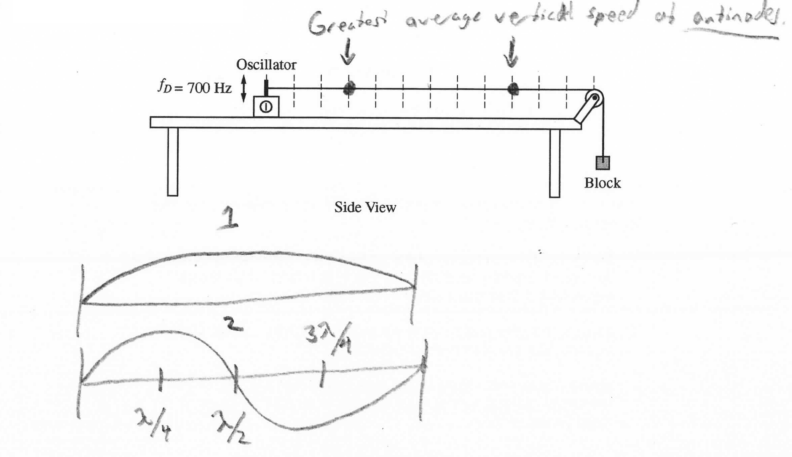
(c) The frequency of the oscillator connected to string D is changed so that the string vibrates in its second harmonic. On the side view of string D below, mark and label the points on the string that have the greatest average vertical speed.
▶️Answer/Explanation
Ans:
\(\frac{\lambda }{2} = L\)
\(\lambda =2L\)
\(\lambda f =v\)
\(f = \frac{v}{\lambda }\)
\(f = \frac{\sqrt{f_{T }}}{\sqrt{m/L}}.\frac{1}{2L}\)
By manipulating the equation given and fλ = v, it can be found that \(f = \frac{\sqrt{f_{T }}}{\sqrt{m/L}}.\frac{1}{2L}\). Since FT and L are the same for all four strings, this means that the frequency changed based on the linear mass density of each storing. So all four string have different linear mass densities.
(b) As was found in part a), \(f\alpha \frac{1}{\sqrt{m/L}}\) , so \(f^{2}\alpha \frac{1}{\sqrt{m/L}}\) since the tension in the string out the length of the string are constant. Therefore, to graph f as a function of \( \frac{1}{\sqrt{m/L}}\) (as the student has done) would not yield a linear graph. Since \(f\alpha \sqrt{m/L}\), the graph would appear to be a sideways parabola, concave down for all values of (m/L) – so definitely not linear . \(f\alpha \frac{1}{m/L}\)
Question: (7 points, suggested time 13 minutes)
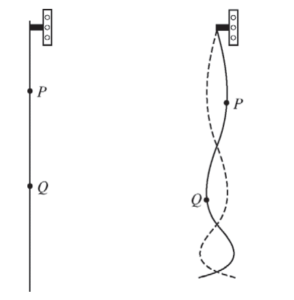
The figure above on the left shows a uniformly thick rope hanging vertically from an oscillator that is turned off. When the oscillator is on and set at a certain frequency, the rope forms the standing wave shown above on the right. P and Q are two points on the rope.
(a) The tension at point P is greater than the tension at point Q. Briefly explain why.
(b) A student hypothesizes that increasing the tension in a rope increases the speed at which waves travel along the rope. In a clear, coherent paragraph-length response that may also contain figures and/or equations, explain why the standing wave shown above supports the student’s hypothesis.
▶️Answer/Explanation
Ans:
(a) 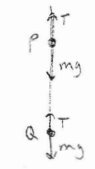
Point P is closer to the oscillator and therefore has a greater mass hanging below it. The force of tension is equal and opposite to the force of gravity, so since Fg = mg and the mass is greater at point P than point Q, the Ft is greater at point P than point Q. FT = – Fg
(b) The wavelength (λ ) at point P is greater than that at point Q. Since V ∝ λ as shown by v = λf, the velocity at point P must also be greater than point Q. Since point p are point Q are or the same string and only their tensions differ, the greater tension at point P correlates with the greater wavelength and therefore speed.
Question: (7 points, suggested time 13 minutes)
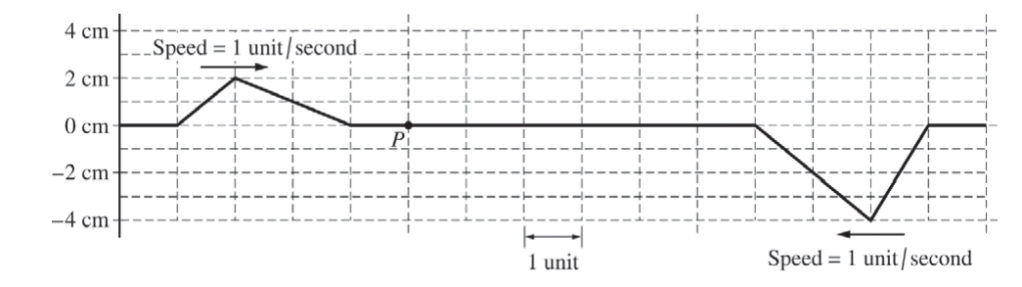
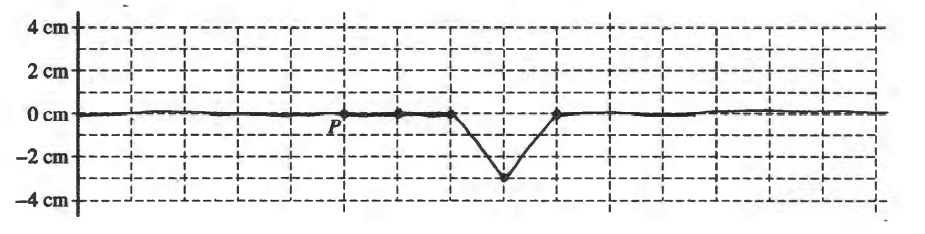
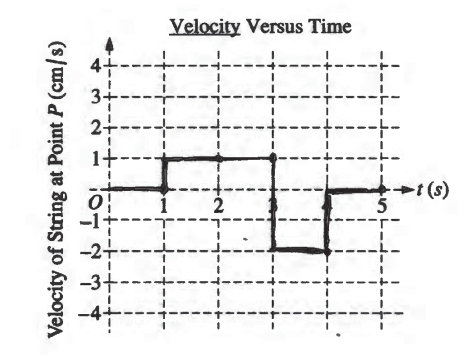
Two wave pulses are traveling in opposite directions on a string. The shape of the string at t = 0 is shown above. Each pulse is moving with a speed of one unit per second in the direction indicated.
(a) Between time t = 0 and t = 5 seconds, the entire left-hand pulse approaches and moves beyond point P on the string. On the coordinate axes below, plot the velocity of the piece of string located at point P as a function of time between t = 0 and t = 5 seconds.
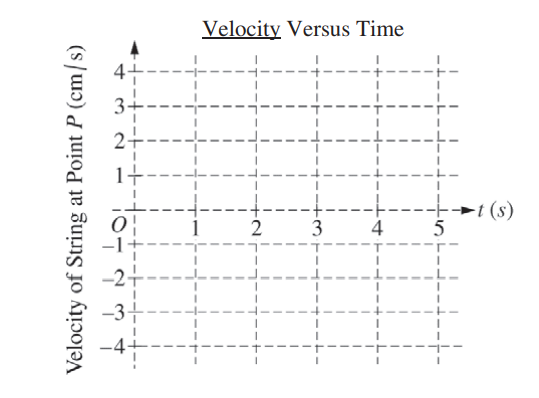
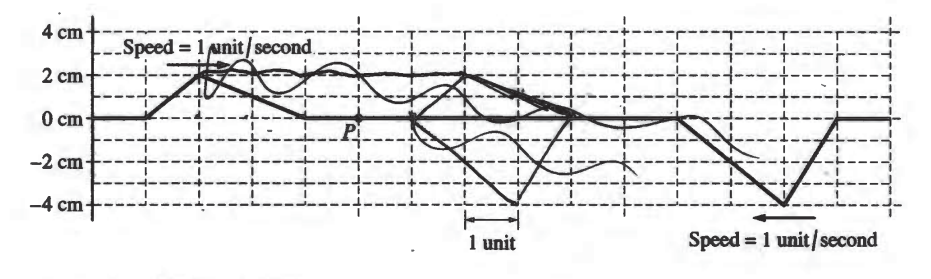
(b) At t = 5 s, the pulses completely overlap. On the grid provided below, sketch the shape of the entire string at t = 5 s.
Note: Do any scratch (practice) work on the grids on the following page. You will only be graded for the sketch made on the grid on this page.
The grids below are provided for scratch work only. Sketches made below will NOT be graded.
▶️Answer/Explanation
Ans:
(a)
(b)