Question: (10 points – suggested time 20 minutes)
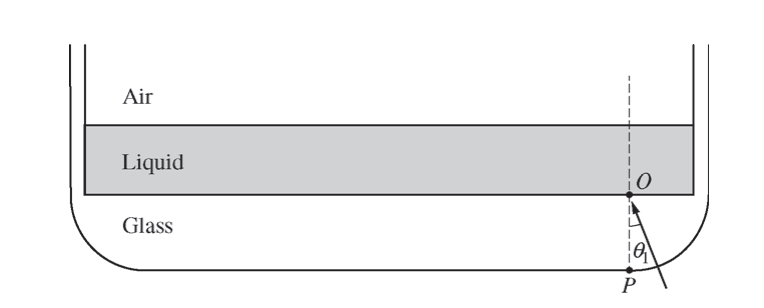
The figure above shows a cross section of a drinking glass (index of refraction 1.52) filled with a thin layer of liquid (index of refraction 1.33). The bottom corners of the glass are circular arcs, with the bottom right arc centered at point O. A monochromatic light source placed to the right of point P shines a beam aimed at point O at an angle of incidence θ . The flat bottom surface of the glass containing point P is frosted so that bright spots appear where light from the beam strikes the bottom surface and does not reflect. When θ = θ1, two bright spots appear on the bottom surface of the glass. The spot closer to point P will be referred to as X; the spot farther from P will be referred to as Y. The location of spot X and that of spot Y both change as θ is increased.
(a) In a coherent paragraph-length answer, describe the processes involved in the formation of spots X and Y when θ = θ1 . Include an explanation of why spot Y is located farther from point P than spot X is and what factors affect the brightness of the spots.
(b) When θ is increased to θ2 , one of the spots becomes brighter than it was before, due to total internal reflection.
i. On the figure below, draw a ray diagram that clearly and accurately shows the formation of spots X and Y when θ = θ2.
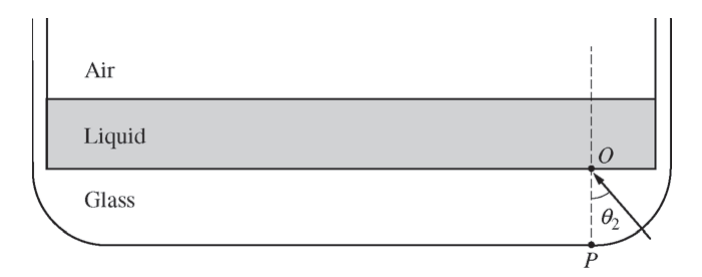
ii. Which spot, X or Y, becomes brighter than it was before due to total internal reflection? Explain your reasoning.
(c) When θ is further increased to θ3, one of the spots disappears entirely.
i. On the figure below, draw a ray diagram that clearly and accurately shows the formation of the remaining spot, X or Y, when θ = θ3 .
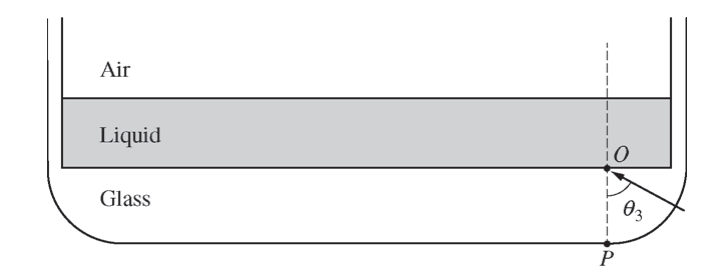
ii. Indicate which spot, X or Y, disappears. Explain your reasoning in terms of total internal reflection.
▶️Answer/Explanation
Ans:
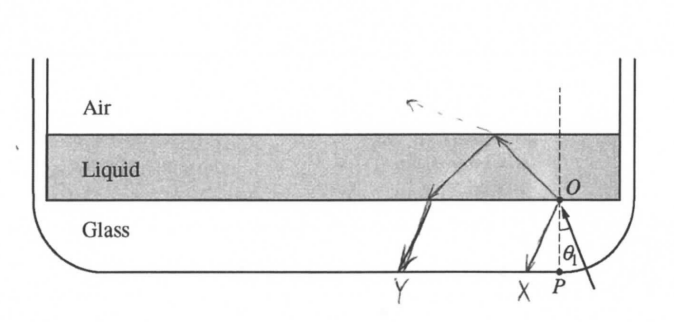
Spot X is formed by the light that bounces off of the liquid and directly onto the bottom of the glass. Spot Y is formed by the light that passes through the glass, into the liquid (refracted) then bounces off of the air-liquid boundary back into the liquid and is then refracted by the glass after passing through it making a spot on the bottom. The amounts of light that are a each stage reflected, refracted determines the spot brightness and the light that firms Y travels further horizontally as the liquid refracts and reflects it further than that of spot X.
(b) i.
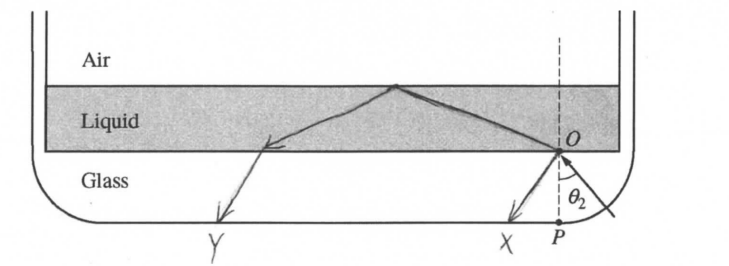
ii.
At some angle θ2 that angle within the liquid passes the critical angle after which there is total internal (reflection off of the air so more light gets reflected, making Y brighter.
(c)
i.
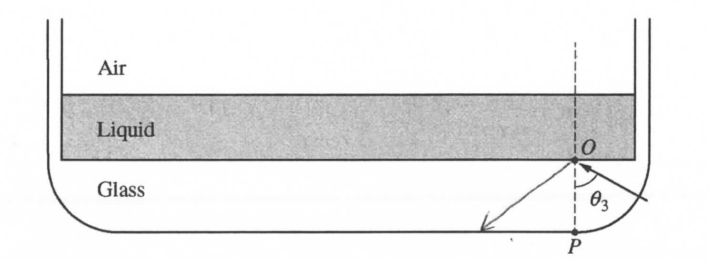
ii.
At θ3 the critical angle for the glass liquid boundary is surpassed and the light is totally internally reflected so some of it can create Y, so it dissappears.
Question: (10 points – suggested time 20 minutes)

The figure above shows a cross section of a drinking glass (index of refraction 1.52) filled with a thin layer of liquid (index of refraction 1.33). The bottom corners of the glass are circular arcs, with the bottom right arc centered at point O. A monochromatic light source placed to the right of point P shines a beam aimed at point O at an angle of incidence θ . The flat bottom surface of the glass containing point P is frosted so that bright spots appear where light from the beam strikes the bottom surface and does not reflect. When θ = θ1, two bright spots appear on the bottom surface of the glass. The spot closer to point P will be referred to as X; the spot farther from P will be referred to as Y. The location of spot X and that of spot Y both change as θ is increased.
(a) In a coherent paragraph-length answer, describe the processes involved in the formation of spots X and Y when θ = θ1 . Include an explanation of why spot Y is located farther from point P than spot X is and what factors affect the brightness of the spots.
(b) When θ is increased to θ2 , one of the spots becomes brighter than it was before, due to total internal reflection.
i. On the figure below, draw a ray diagram that clearly and accurately shows the formation of spots X and Y when θ = θ2.

ii. Which spot, X or Y, becomes brighter than it was before due to total internal reflection? Explain your reasoning.
(c) When θ is further increased to θ3, one of the spots disappears entirely.
i. On the figure below, draw a ray diagram that clearly and accurately shows the formation of the remaining spot, X or Y, when θ = θ3 .

ii. Indicate which spot, X or Y, disappears. Explain your reasoning in terms of total internal reflection.
▶️Answer/Explanation
Ans:

Spot X is formed by the light that bounces off of the liquid and directly onto the bottom of the glass. Spot Y is formed by the light that passes through the glass, into the liquid (refracted) then bounces off of the air-liquid boundary back into the liquid and is then refracted by the glass after passing through it making a spot on the bottom. The amounts of light that are a each stage reflected, refracted determines the spot brightness and the light that firms Y travels further horizontally as the liquid refracts and reflects it further than that of spot X.
(b) i.

ii.
At some angle θ2 that angle within the liquid passes the critical angle after which there is total internal (reflection off of the air so more light gets reflected, making Y brighter.
(c)
i.

ii.
At θ3 the critical angle for the glass liquid boundary is surpassed and the light is totally internally reflected so some of it can create Y, so it dissappears.
Question
A ray of light is incident on an unknown transparent substance from the air. The angle of incidence is 40°, and the angle of refraction is 22°.
(a) Explain why these measurements indicate that a change in speed must be happening as the light changes medium. Qualitatively justify whether the speed of light in the unknown transparent substance is higher or lower than that of air.
(b) Calculate the absolute index of refraction for this substance. Calculate the velocity of light in this substance.
(c) The substance is now submerged in glycerol ( n = 1.47). Calculate the critical angle of incidence for light going from the unknown substance into glycerol. Explain why there is no critical angle when going the other way, from glycerol into the substance.
(d) The substance is now shaped into a convex lens. How does the focal length of this lens compare with the focal length of a similar-shaped lens made out of crown glass ( n = 1.52)? Justify your answer.
▶️Answer/Explanation
Ans:
(a) The change in angle as the ray of light changes medium is due to a change in speed. Just as a rolling cylinder will pivot if one end of it comes into contact with a rougher surface, so too will the ray of light pivot as it changes speed when crossing from one medium into another. Since the light is pivoting toward the normal, the new medium must be a slower one.
(b) Use: \(n_{1}\sin \theta _{1}=n_{2}\sin \theta _{2}\)
Since air has the index of refraction \(n_{1}\) = 1.00, we have:
\(n_{2}=\frac{\sin \theta _{1}}{\sin \theta _{2}}=\frac{\sin 40^{\circ}}{\sin 22^{\circ}}=1.72\)
Use the relationship between velocity and index of refraction to find the new speed:
v = c / n = (3 × \(10^{8}\))/1.72 = 1.74 × \(10^{8}\) m/s
(c) For the critical angle, we know that the angle of refraction will be 90°:
\(\sin \theta _{c}=n_{2}/n_{1}=\) 1.47/1.74 = 0.8448
\(\theta _{c}=\) 58°
There was no critical angle when reversing the direction because total internal reflection can happen only when going from a slower medium to a faster one (i.e., higher n to lower n ). This is so because going from a slower medium to a faster medium refracts the light away from the normal, toward the surface. This creates a limiting case (called the critical angle) that refracts light all the way to the surface itself (90- degree refraction). Angles beyond this don’t work; no refraction occurs. When going from a faster medium to a slower medium, the light ray refracts toward the normal. So there is always a refracted solution and, hence, no critical angle.
(d) The focal length of the lens made from the unknown substance will be shorter than the focal length of the lens made from crown glass. Since the index of refraction of the unknown substance is greater than that of crown glass, light will refract more. Thus the converging point for the focal length will be closer to the lens.
Question: (12 points, suggested time 25 minutes)
A student is given a glass block that has been specially treated so that the path of light can be seen as the light travels through the glass. The student is asked to design an experiment to measure the index of refraction of the glass. The light source available in the laboratory is a hydrogen lamp that emits red light of a known wavelength.
(a) A linear graph is to be used to determine the index of refraction of the glass. Indicate the quantities that should be graphed and describe how the graph could be used to determine the index of refraction of the glass.
(b) Outline an experimental procedure that could gather the necessary data. Include sufficient detail so that another student could follow your procedure. In addition to the glass block and the hydrogen lamp, the equipment in a typical classroom laboratory is available.
(c) Predict how the path of the light will change as it enters the glass. Support your prediction using a qualitative comparison of the speed of light in glass and the speed of light in air.
(d) Describe the process(es) by which red light from the lamp is produced by hydrogen atoms that are initially in the ground state. Draw and label an energy level diagram that supports the atomic process(es) you describe.
▶️Answer/Explanation
Ans:
n1Sinθ1 = n2Sinθ2 n1 drops out as it is equal to 1 in air.
Sinθ1 = n2Sinθ2 n2 should be solved for as it is the unknown.
\(n_{2} = \frac{Sin\theta _{1}}{Sin\theta _{2}}\) Thus Sinθ1 should be graphed on the y-axis and Sinθ2 should be graphed on the x-axis, so that n2 is equal to \(\frac{y}{x}\) on the slope of the graph.
(b)
The lamp should be set up using a slip so that only a thin beam of light is emitted. The glass block should be in line with this beam and placed on a turnable surface independent of the rest of the apparatus. Measurements can then be made by using a protractor to measure the angle the beam of light makes with the glass block just before entering, and the angle the beam of light makes with the glass block just after entering. All angles should be measured from the normal line. The first angle measured, or the N incident angle N, should be changed so that multiple measurements can be taken.
(c)
The path of the light will bend toward the normal line so that the angle of refraction is less than the angle of incidence. Looking at n1Sinθ1 = n2Sinθ2 we can see that when the index of refraction, n2, is greater than n1 then Sinθ2 must be less than Sinθ1 . Thus θ2< θ1 . The speed of light as it travels through glass is less than the speed of light as it travels through air. Therefore, since \(n = \frac{C}{V}\), when V is less n must increase. Thus nglass is greater than nair.
(d)
Hydrogen atoms in the ground state are excited by other photons. The atoms move to higher energy states as a result of being excited and gaining energy from the photons. The atoms then drop to lower energy states or the ground state and release some or all of the energy they absorbed, respectively.
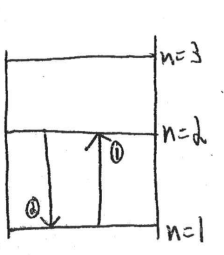
In step 1 energy is absorbed by the atom and it is excited to a higher energy level. In step 2 the energy is released in the form of a photon.
The atom could have also been excited of n=3 and then dropped to eithter n=2 or n=1. If it dropped to n=2 and then for n=1 the atom would release a photon for times – once for each energy level change
