Question
Some scientists want to perform electron diffraction experiments on crystals that have an intermolecular spacing of about \(10^{-10}\) m. They have two processes by which they can produce energetic electrons that can strike the crystals.
Process 1 is the beta decay of potassium into calcium: 
The mass of 
is 39.964000 u and the mass of 
is 39.962591 u. As an approximation, assume that the mass of the neutrino is negligible and that all the decay energy is acquired by the electron.
Process 2 is the emission of electrons when electromagnetic radiation of wavelength 7.5 nm shines on a copper surface with work function 4.7 eV.
(a) Describe a single criterion for determining whether each of these processes can be used to produce electrons for the diffraction experiments.
(b) Determine whether each of these processes could be used to produce electrons appropriate for the diffraction experiments. Justify your answers mathematically.
▶️Answer/Explanation
Ans:(a) For indicating an appropriate quantity to compare — either length or energy
For indicating the appropriate specic quantities to compare: de Broglie wavelengths of electrons and crystal spacing
OR
kinetic energy of electrons and kinetic energy needed to have a de Broglie wavelength equal to the crystal spacing
Example: The energy of electrons produced by each method is comparable to the energy of electrons with de Broglie wavelengths corresponding to the crystal spacing.
(b) For converting the electron energies to de Broglie wavelengths
OR
using the crystal spacing as a de Broglie wavelength to determine
the required electron energy Decay process
For determining the mass difference of the atoms
For converting the mass difference to energy
For correctly evaluating the energy against the crystal Photoelectric process
For determining the energy of the incident light
For determining the maximum kinetic energy K of the ejected electrons
For correctly evaluating the kinetic energy against the crystal
Example: Determine the electron kinetic energy needed for the electron to have a de Broglie
wavelength of\(10^{-10}\) m :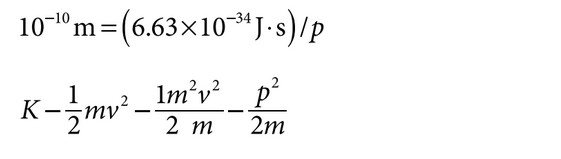
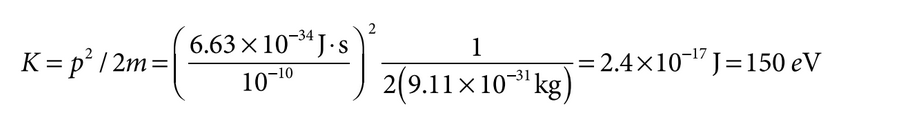
Determine the energy released by the decay reaction, which is converted to kinetic energy of the electron:
NOTE: is is four orders of magnitude larger than , so the wavelength will be two orders of magnitude smaller than desired. is process will not work well. Determine the maximum kinetic energy K of electrons emitted in the photoelectric effect: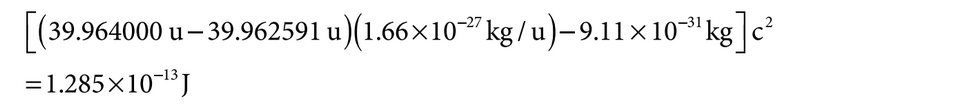 
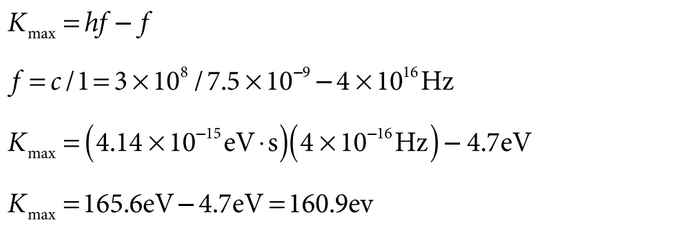
NOTE: is is comparable to 150 eV, so this process will work.
Question: (12 points, suggested time 25 minutes)
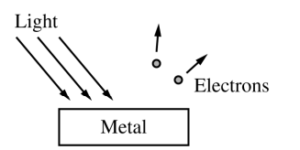
Monochromatic light of frequency f shines on a metal, as shown above. The frequency of the light is varied, and for some frequencies electrons are emitted from the metal. The maximum kinetic energy Ke of the emitted electrons is measured as a function of the frequency of the light.
(a)
i. Based on conservation of energy, the relationship between Ke and f is predicted to be Af = B + Ke when f > f0 and Ke = 0 when f ≤ f0, where A and B are positive constants. A graph of this relationship is shown below. Indicate which aspects of the graph correspond to A and B. Also, explain the physical meaning of A, B, and f0 .
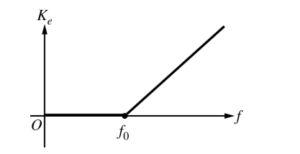
ii. Explain the physical meaning of the horizontal section of the graph between the origin and f0 .
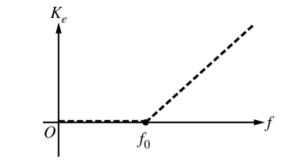
iii. A second metal with different properties than the first metal is now used. On the figure below, the dashed lines are the same lines shown in the previous graph. Sketch lines on the figure below that could represent the data for the second metal. Explain one difference between the two graphs.
(b) The figure below shows an electroscope. A sphere is connected by a vertical bar to the leaves, which are thin, light strips of material. The sphere, leaves, and bar are all made of metal. The electroscope initially has a negative charge, so the leaves are separated.
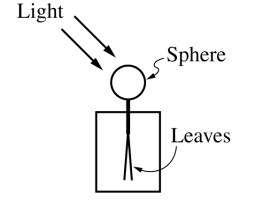
i. Ultraviolet (UV) light shines on the sphere, causing the leaves of the electroscope to move closer together. Explain why this happens.
ii. Green light then shines on an identical negatively charged electroscope. No movement of the leaves is observed. Explain why the green light does not make the leaves move, while the UV light does.
(c) The brightness of the green light is increased until the intensity (power per unit area) is the same as that of the UV light. What aspect of the green light changes when its brightness is increased? Would shining the brighter green light on the electroscope result in movement of the leaves? Explain why or why not.
▶️Answer/Explanation
Ans:
(a)
i.
A is represented by the slope of the graph B is represented by the y-intercept of the graph A is equal to Planck’s constant and determines the energy of a photon given it’s frequency B is the work function, or amount of energy required to release an election from the nucleus of one of the metal atoms. F0 is the minimum frequency required to have enough energy to overcome the work function.
ii.
The horizontal section represents the range of frequencies that don’t have enough energy to overcome the work function, therefore the election does not have enough energy to break away from the nucleus. Since the election is never emmited, Ke cannot be measured.
iii.
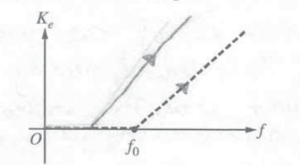
The horizontal section for the graph of a different metal could be different because it could have a lower work function.
(b)
i.
Due to the photoelectric effect, when light hits the sphere, some elections in the sphere absorb enough energy from the photons to be emmited. With less total elections, there is less total negative charge, reducing the repulsive electrostatic force between the leaves, reducing their separation.
ii.
The UV light has a higher frequency than the green light, therefore higher energy. The green light does not give the elections enough energy to overcome the work function of the metal, or energy required to emmit the elections. Therefore no charge is lost because no elections are lost. The UV light has enough energy to overcome the work function.
(c)
When the brightness of the green light is increased its intensity is increased, meaning more photons are released per unit area. The increase in brightness would not result in movement of the leaves. The change in intensity only change the amount of photons preset and does not change the energy per photon. Each photon would still lack the energy to overcome the work function meaning no elections would be released. Meaning the leaves wouldn’t move.
Question
The electron energy levels above are for an electron confined to a certain very small one-dimensional region of space. The energy En of the levels, where n = 1, 2, 3, … , is given by En = n2E1 . Express all algebraic answers in terms of E1 and fundamental constants.
(a) On the diagram above, label the three excited energy levels with the values for their energies in terms of E1, the energy of the ground state.
(b) Calculate the smallest frequency of light that can be absorbed by an electron in this system when it is in the ground state, n = 1.
(c) If an electron is raised into the second excited state, draw on the diagram all the possible transitions that the electron can make in returning to the ground state.
(d) Calculate the wavelength of the highest energy photon that can be emitted in the transitions in part (c).
▶️Answer/Explanation
Ans:
a) From the given formula, the energy levels 1,2,3 correspond to E1, 4E1, 9E1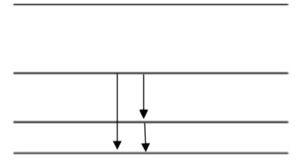
n=3, 9E1
n=2, 4E1
n=1, E1
b) Smallest frequency absorption corresponds to the smallest energy difference, which is n2–n1 = 3E1. The frequency of this absorption can be determined from E=hf … 3E1 = hf … f = 3E1 / h
c) The second excited state is n=3, there are three possible transitions to the ground state shown above.
d) The highest energy emission corresponds to n3→n1 … ∆E = 8E1. The wavelength of this photon can be found with E = hc / λ … 8E1 = hc / λ … λ = hc/ 8E1