Question
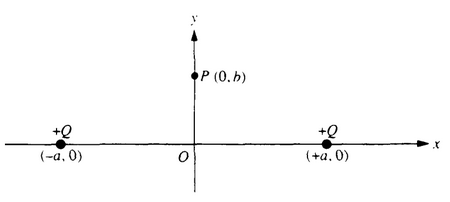
Two equal positive charges Q are fixed on the x-axis. one at +a and the other at -a, as shown
above. Point P is a point on the y-axis with coordinates (0, b ). Determine each of the following in
terms of the given quantities and fundamental constants.
a. The electric field E at the origin O
b. The electric potential V at the origin O.
c. The magnitude of the electric field E at point P.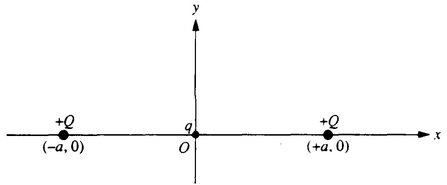
A small particle of charge q (q << Q ) and mass m is placed at the origin, displaced slightly, and then
released. Assume that the only subsequent forces acting are the electric forces from the two fixed
charges Q. at x = +a and x = -a. and that the particle moves only in the xy -plane. In each of the
following cases, describe briefly the motion of the charged particle after it is released. Write an
expression for its speed when far away if the resulting force pushes it away from the origin.
d. q is positive and is displaced in the +x direction.
e. q is positive and is displaced in the +y direction.
f. q is negative and is displaced in the +y direction.
Answer/Explanation
Ans:
a. From each charge \(E=kQ/r^2\), but at the origin, the vectors form the two charges point in opposite directions and cancel so E = 0
b. V = kQ/a + kQ/a = 2kQ/a
c. Due to each charge \(E=kQ/r^2=kQ/(a^2+b^2)\), but the x components cancel so we only need to add the y components \(E_y=[kQ/(a^2+b^2)] sin ]\theta=[kQ/(a^2+b^2)]b/(a^2+b^2)^P+{1/2}\) which gives \(E=2kQb/(a^2+b^2)^{3/2}\)
d. The particle will repel from the closer charge and move through the origin until it repelled and reversed by the charge on the other side of the origin. The particle will oscilalte about the origin.
e. The particle will move away from the origin
\(U=2kQq/a=1/2 mv^2\) giving \(v =2(kQq/ma)^{1/2}\)
f. The particle will oscillate about the origin
Question
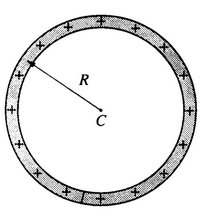
A thin nonconducting rod that carries a uniform charge per unit length of λ is bent into a circle of
radius R. as shown above. Express your answers in terms of λ, R. and fundamental constants.
a. Determine the electric potential V at the center C of the circle.
b. Determine the magnitude E of the electric field at the center C of the circle.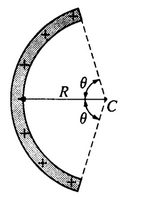
Another thin nonconducting rod that carries the same uniform charge per unit length λ is bent into an
arc of a circle of radius R. which subtends an angle of 2θ, as shown above. Express your answers in
terms of λ and the quantities given above.
c. Determine the total charge on the rod.
d. Determine the electric potential V at the center of curvature C of the arc.
e. Determine the magnitude E of the electric field at the center of curvature C of the arc. Indicate the
direction of the electric field on the diagram above.
Answer/Explanation
Ans:
a. V = ΣkQ/r and since all the charge is equidistant from the center we get V = kQ/R where Q = λL = λ2πR so
V = 2πkλ
1994E1
b. The electric field from each infinitesimal piece of the ring is cancelled from a piece on the opposite side of the
ring. E = 0
c. The total charge on the rod is the charge per unit length times the length of the rod: L = 2Rθ so Q = 2Rθλ
d. As in part a, the charge is all equidistance so we substitute the new amount of charge into the expression
V = 2kθλ
e. \(E=kQ/R^2\), all of the charge is equidistant, but we must take direction into account. The y components will cancel so we only need to consider the x (horizontal) component from each infinitesimal element ](dq = \lambda R d \theta\)
\(E=\int_{-\theta}^{\theta}\frac{kdq}{R^2}cos \theta d\theta = \int_{-\theta}^{\theta}\frac{kd\lambda R}{R^2}cos \theta d \theta=\int_{-\theta}^{\theta}\frac{k\lambda}{R}cos \theta d\theta =\frac{k\lambda}{R}sin \theta |^\theta_{-\theta}=\frac{2k\lambda}{R}sin \theta\)
pointing to the right
