Question
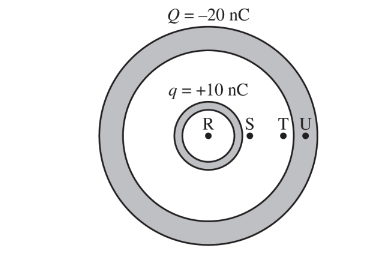
Two concentric spherical conducting shells and four labeled points are shown above. The outer shell has a net charge Q = −20 nC. The inner shell has a net charge q = +10 nC.
The magnitudes of the electric fields at the four labeled points in the figure are \(E_R\), \(E_S\), \(E_T, \)and\( E_u\), respectively. Which of the following correctly ranks the points according to the magnitude of their electric fields?
(A) \(E_R=E_S= E_T = E_U\)
(B)\( E_s > E_T > (E_R = E_U)\)
(C)\( (E_s = E_T) > E_U > E_R\)
(D)\( E_T > E_s > E_R > E_U\)
(E) \((E_s = E_T)>(E_R = E_U)\)
Answer/Explanation
Ans:B
Applying Gauss’s law and using Gaussian surfaces as described, \(E_R= E _U = 0\) because no charge is enclosed by the respective Gaussian sphere. (The sphere for point U is centered at
the shells’ center; the sphere for point R is centered slightly off the shells’ center but still encloses no charge.) \(E_ s >E_U > 0 \)because the same +10nC charge is enclosed by the
Question(a) – (c)
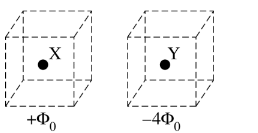
The figure above shows two charged spherical conductors, X and Y, which are equal in size. When each conductor is isolated and surrounded by a closed cubical surface, the total electric flux
through the surfaces is \(+Φ_0\) for conductor X and \(−4Φ_0\) for conductor Y.
Question(a)
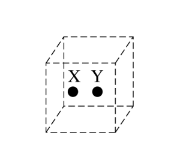Conductor Y is brought into contact withconductor X and then separated. If the separation is small so that both conductors are inside the same closed cubical surface, as shown above, what is the total electric flux through the surface?
(A) \(-3\Phi _{0}\)
(B)\(-\frac{5}{2}\Phi _{0}\)
(C)\(-\frac{3}{2}\Phi _{0}\)
(D) \(\frac{5}{2}\Phi _{0}\)
(E) It cannot be determined without knowing the distance separating the two conductors and the individual charges on each.
Answer/Explanation
Ans:A
Question(b)
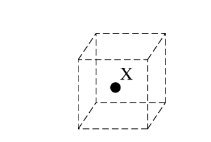
After being brought into contact with conductor X, conductor Y is moved a very large distance away from conductor X. What is the total electric flux through a closed cubical surface surrounding conductor X, as shown above?
(A)\(-3\Phi _{0}\)
(B)\(-\frac{3}{2}\Phi _{0}\)
(C)\(\frac{1}{2}\Phi _{0}\)
(D)\(\frac{3}{2}\Phi _{0}\)
Answer/Explanation
Question(c)
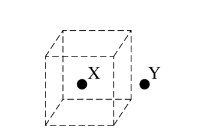
Conductor Y is then moved closer to conductor X until it is just outside a closed cubical surface containing conductor X, as shown in the figure above. How would the total electric flux through the cubical surface change as conductor Y is moving?
(A) It would increase.
(B) It would decrease.
(C) It would change sign.
(D) It would remain constant, with the flux through each side of the surface also remaining constant.
(E) It would remain constant, but the flux through each side of the cubical surface would change.