Question
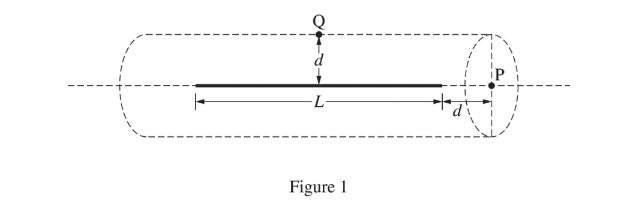
A thin wire of length L has a uniform charge density \(=\lambda \). A cylindrical Gaussian surface of radius d is drawn with the wire along its central axis, as shown above. Point P is located at the center of one end of the cylinder, a distance d from the end of the wire. Point Q is on the edge of the cylinder directly above the center of the wire, as shown above. A student says, “Gauss’s law can be used to find the electric flux \( \Phi \)through the Gaussian surface.”
(a) Is the student’s statement correct or incorrect? ____ Correct ____ Incorrect If you have chosen “Correct,” use Gauss’s law to find the electric flux F through the Gaussian surface. If you have chosen “Incorrect,” explain why the student’s reasoning is incorrect and why Gauss’s law cannot be applied in this situation.
(b) Two students discuss whether or not they can use Gauss’s law to find the electric field at points P and Q. At which of the points, if either, is Gauss’s law a useful method for finding the electric field? _____ At point P only ____ At point Q only _____ At both points P and Q ____ At neither point P nor point Q Justify your answer.
(c) Assuming the electric potential is zero at infinity, show that the value for the electric potential at point P is given by the following expression.
\(v=\frac{\lambda }{4\pi \varepsilon _0}In(\frac{L+d}{d})\)
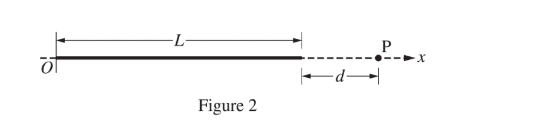
The wire is aligned along the x-axis with the origin at the left end of the wire, as shown in Figure 2 above.
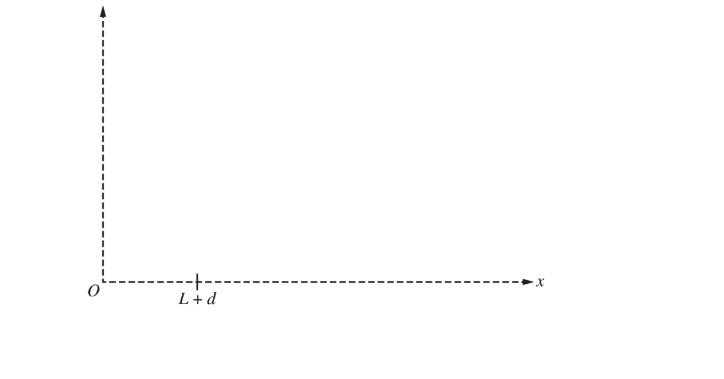
(d) A positively charged particle of charge +e and mass m is released from rest at point P. On the axes below, sketch the kinetic energy K of the particle, the potential energy U of the wire-particle system, and the total energy \(E_{tot}\) of the wire-particle system as functions of the particle’s position x. Clearly label each sketch with K, U, and E tot . Explicitly label any maximum with numerical values or algebraic expressions, as appropriate.
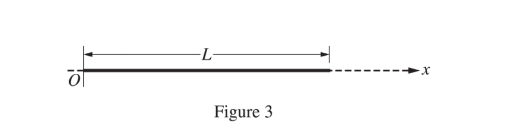
(e) Derive an expression for the magnitude of the electric field due to the wire as a function of the position along the x-axis, where x > L . Express your answer in terms of x, L, l , and physical constants, as appropriate.
Answer/Explanation
(a) Select “Correct” Note: If the wrong selection is made, the explanation is ignored. For using an appropriate equation to calculate the flux
Claim: Student is correct.
Evidence: A cylinder is useful for Gauss’s law.
Reasoning: A cylindrical surface has geometric symmetry.
(b) Select “At neither point P nor point Q” or “At point Q only”
Note: If the wrong selection is made, the justification is ignored.
For a justification consistent with selection above
Example: There is no simple way to write the electric field at point P or Q in terms of
the flux due to cylinder extending beyond the line of charge.
Example: By drawing a new Gaussian cylinder that does not extend beyond the line of
charge, Gauss’s law can be used to calculate the electric field at point Q.
(c) For indicating an attempt to integrate to determine the electric potential at P\( V=\int \frac{1}{4\pi\varepsilon _0r}dq\)
For integrating in terms of distance
\(Q=\lambda L\therefore =dq=\lambda dr\therefore V=\int_{r=d+L}^{r=d}\frac{\lambda }{4\pi\varepsilon _0}dr\)
For integrating using the correct limits or constant of integration \(V=\frac{\lambda }{4\pi\varepsilon _0}[ln(r)]_{r=d}^{r=d+L}=\frac{\lambda }{4\pi\varepsilon _0}(ln(d+L))-ln(d))=\frac{\lambda }{4\pi\varepsilon _0}ln\left ( \frac{d+L}{d} \right )\)
(d) For a curve in the first quadrant label K that is increasing in value for x >L + d point For a curve that is concave down curve starting at the point ( L +d , 0) and approaching a horizontal line
For a curve in the first quadrant label U that is decreasing in value for x> L + d point For a concave up curve at L + d starting at or near the maximum value and approaching the x-axis
For a horizontal line labeled\( E_{tot}\) that is at the maximum value 1 point For labeling and using correct asymptotes for the K and U curves
(e)

Question
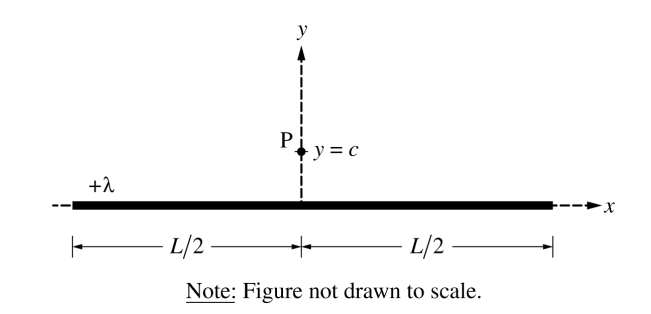
A very long, thin, nonconducting cylinder of length L is centered on the y-axis, as shown above. The cylinder has a uniform linear charge density + λ . Point P is located on the y-axis at y c = , where L >> c .
(a)
i. On the figure shown below, draw an arrow to indicate the direction of the electric field at point P due to the long cylinder. The arrow should start on and point away from the dot.
ii. Describe the shape and location of a Gaussian surface that can be used to determine the electric field at point P due to the long cylinder.
iii. Use your Gaussian surface to derive an expression for the magnitude of the electric field at point P. Express your answer in terms of λ , c, L, and physical constants, as appropriate.
(b) A proton is released from rest at point P. On the axes below, sketch the velocity v as a function of position y and the acceleration a as a function of position y for the proton.
The original cylinder is now replaced with a much shorter thin, nonconducting cylinder with the same uniform linear charge density + λ , as shown in the figure below. The length of the cylinder to the right of the y-axis is a, and the length of the cylinder to the left of the y-axis is b, where a < b .
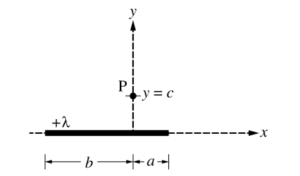
(c) On the figure shown below, draw an arrow to indicate the direction of the electric field at point P due to the shorter cylinder. The arrow should start on and point away from the dot.
(d)
i. Is there a single Gaussian surface that can be used with Gauss’s law to derive an expression for the electric field at point P?
____ Yes ____ No
ii. If your answer to part (d)(i) is yes, explain how you can use Gauss’s law to derive an expression for the field at point P. If your answer to part (d)(i) is no, explain why Gauss’s law cannot be applied to derive an expression for the electric field in this case.
A student in class argues that using the integral shown below might be a useful approach for determining the electric field at point P.
\(E = \int \frac{1}{4\pi\varepsilon _{0}r^{2}}\frac{1}{r^{2}}dq\)
The student uses this approach and writes the following two integrals for the magnitude of the horizontal and vertical components of the electric field at point P.
Horizontal component: \(\left | E_{x} \right |=\frac{\lambda }{4\pi \varepsilon _{0}}\int_{-b}^{a}\frac{x}{\left ( c^{2}+x^{2} \right )^{3/2}}dx\)
Vertical component: \(\left | E_{y} \right |=\frac{\lambda }{4\pi \varepsilon _{0}}\int_{-b}^{a}\frac{x}{\left ( c^{2}+x^{2} \right )}dx\)
(e)
i. One of the two expressions above is not correct. Which expression is not correct?
____ Horizontal component ____ Vertical component
ii. Identify two mistakes in the incorrect expression, and explain how to correct the mistakes.
Answer/Explanation
Ans:
(a) i.
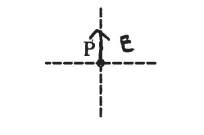
ii.
A cylindric gaussian surface with its center and corner on the long cylinder can be used to determine electric field.
iii.
\(\int \overrightarrow{E}\cdot d\overrightarrow{S}=\frac{q_{enc}}{\varepsilon _{0}}\)
\(E(2\pi rL)=\frac{XL}{\varepsilon _{0}}\) \(E=\frac{X}{2\pi r\varepsilon _{0}}\) \(E(c)=\frac{X}{2\pi r\varepsilon _{0}}\)
(b)
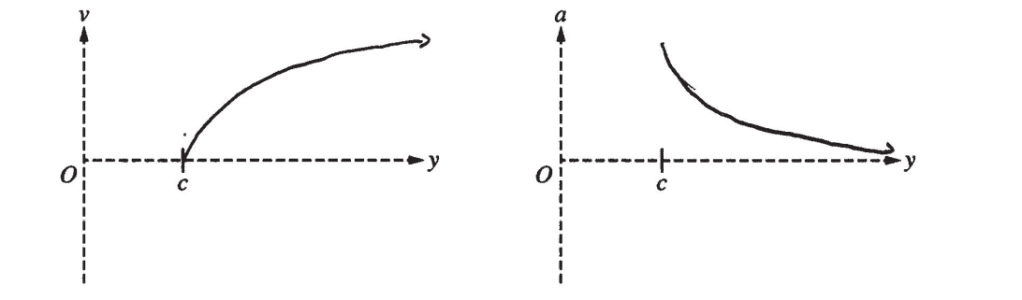
(c)
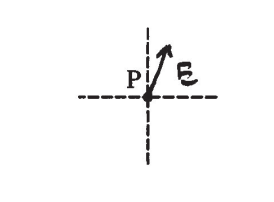
(d)
i. ___√__ No
ii. Because a and b are not much greater than c, the field so no longer ideal once are horizontal components of the field from the cylinder cannot be ignored. Therefore, a simple gaussian surface cannot be used and gauss’s law cannot be applied.
(e)
i. ___√__ Vertical component
ii. In this compression, integer should still be with respect to dx since it D integrating along the since, so the should change it shown dy to dx. Also, denominator of the integral should be to the power of 3/2.
