Question
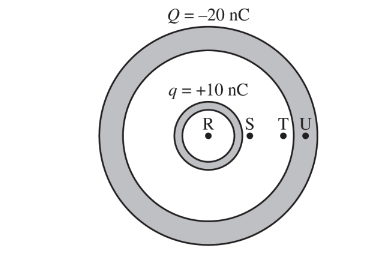
Two concentric spherical conducting shells and four labeled points are shown above. The outer shell has a net charge Q = −20 nC. The inner shell has a net charge q = +10 nC.
What is the charge on the outer surface of the outer shell?
(A) –30 nC
(B) –20 nC
(C) –10 nC
(D) +10 nC
(E) +30 nC
Answer/Explanation
Ans:C
A charge of −10nC on the outer shell is drawn to the shell’s inner surface by the +10nC on the inner shell. The remainderof the charge on the outer shell distributes itself as far away as possible from the −10nC on the shell’s inner surface. Therefore, −10nC is distributed on the outer surface of the outer shell.
Question

Two concentric spherical conducting shells and four labeled points are shown above. The outer shell has a net charge Q = −20 nC. The inner shell has a net charge q = +10 nC.
The magnitudes of the electric fields at the four labeled points in the figure are \(E_R\), \(E_S\), \(E_T, \)and\( E_u\), respectively. Which of the following correctly ranks the points according to the magnitude of their electric fields?
(A) \(E_R=E_S= E_T = E_U\)
(B)\( E_s > E_T > (E_R = E_U)\)
(C)\( (E_s = E_T) > E_U > E_R\)
(D)\( E_T > E_s > E_R > E_U\)
(E) \((E_s = E_T)>(E_R = E_U)\)
Answer/Explanation
Ans:B
Applying Gauss’s law and using Gaussian surfaces as described, \(E_R= E _U = 0\) because no charge is enclosed by the respective Gaussian sphere. (The sphere for point U is centered at
the shells’ center; the sphere for point R is centered slightly off the shells’ center but still encloses no charge.) \(E_ s >E_U > 0 \)because the same +10nC charge is enclosed by the
Question
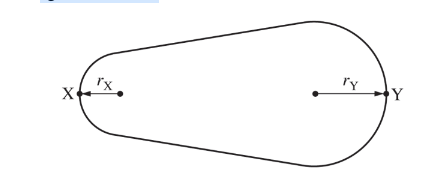
The figure above shows a cross section of a solid, isolated, metallic conductor in electrostatic equilibrium with a net charge +Q. The two ends of the conductor are spherical surfaces of radii \(r_X\) and \(r_Y\) , where\( r_X\) <\( r_Y\) . Points X and Y are on the conductor at each end.
Assuming that the electric potential is zero an infinite distance from the conductor, which of the following statements is true about the magnitude of the electric potential at points X and Y?
(A) It is greater at point X than at point Y.
(B) It is greater at point Y than at point X.
(C) It is zero at both points X and Y.
(D) It has the same nonzero value at both points X and Y.
(E) There is not enough information to determine at which point, if either, the magnitude of the electric potential is greater.</p
Answer/Explanation
Ans:DThe electric field inside a conductor is zero; thus, the electric potential is the same at all points on the conductor’s surface. There is a positive net charge on the conductor. Therefore, a positive
Question
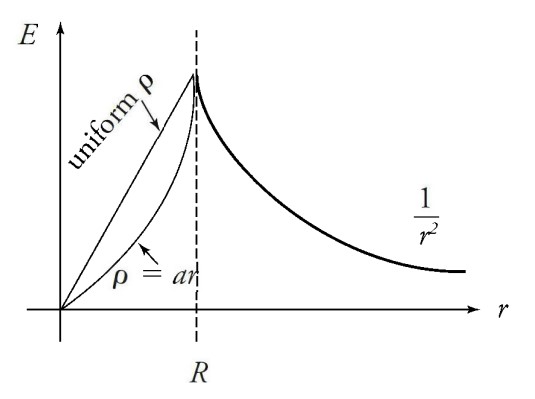
A spherical charge distribution varies with the radius r by the equation p = ar, where p is the volume charge density and a is a positive constant. The distribution goes out to a radius R. Which of the following is true of the electric field strength due to this charge distribution at a distance r from the center?
(A) It increases as r approaches infinity.
(B) It decreases linearly for r > R.
(C) It increases linearly for r > R.
(D) It increases linearly for r < R.
(E) It increases non-linearly for r < R.
Answer/Explanation
Ans :E
The electric field will decrease as \(\frac{1}{r^{2}}\) when r > R. This eliminates (A), (B), and (C). When p is constant for a spherical charge distribution, the electric field strength varies linearly with r for r < R. Therefore, if p increases with r, as in this problem, more charge is being contained as r increases. This will make the electric field increase less rapidly than if p were constant. Therefore, (E) is correct. The general shapes of E vs. r for a uniform p and our problem are shown below. This sketch assumes the total charge is equal for both.