Question
An uncharged parallel-plate capacitor is connected through an open switch to a battery of voltage \(V\). The switch is closed and the capacitor is allowed to charge.
As the capacitor is charged, energy is transferred to it from the battery. When the capacitor is fully charged, the energy stored in the capacitor is \(U_1\). The energy stored in the capacitor when the stored charge is \(\frac{q_0}{2}\) is
(A) \(\frac{1}{4} U_1\)
(B) \(\frac{1}{2} U_1\)
(C) \(U_1\)
(D) \(2 U_1\)
(E) \(4 U_1\)
▶️Answer/Explanation
Ans:D
The energy \( U \) is related to the charge \( q \) by the formula:
\[ U_1 = \frac{1}{2C} q^2 \]
Now, when the stored charge is \( \frac{q_0}{2} \). So, the energy \( U’ \) when the stored charge is \( \frac{q_0}{2} \) is:
\[ U’ = \frac{1}{2C} \left(\frac{q_0}{2}\right)^2 = \frac{1}{8C} q_0^2 \]
Now, let’s find the energy \( U’ \) in terms of \( U_1 \):
\[ U’ = \frac{1}{8} C q_0^2 \]
Now, express \( U’ \) in terms of \( U_1 \):
\[ U’ = \frac{1}{4}U_1 \]
So, the correct answer is (A) \(\frac{1}{4} U_1\).
Question
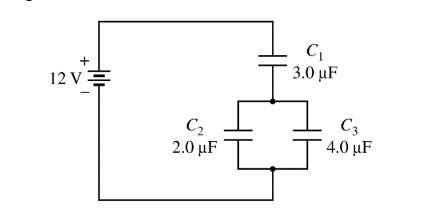
The circuit shown above has three capacitors and a 12 V battery. The capacitors are charged to steady state conditions.
What is the potential difference across capacitor\( C_1\) ?
(A) 3.0 V
(B) 4.0 V
(C) 6.0 V
(D) 8.0 V
(E) 12 V
Answer/Explanation
Ans:D
Question(a)-(b)
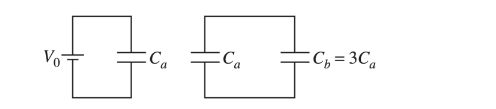
A capacitor of capacitance\( C_a\) is first charged to a voltage V0 , as shown above on the left. Without losing any charge, the capacitor is now disconnected from the voltage source and connected to a second initially uncharged capacitor of capacitance\( C_b\) that is three times \(C_ a\) , and the circuit is allowed to reach equilibrium, as shown above on the right.
Question(b)
The new voltage across capacitor \(C_ a\) is \(V_ a \) . How does this new voltage compare with the original voltage of\( V_0\) ?
(A) \(V _a > V_0\)
(B) \(V_ a < V_0\)
(C) \(V_ a = V_0\)
(D) It depends on the value of \(C _a\) .
(E) It depends on the value of \(C_b \).
Answer/Explanation
Ans:B
Question
A parallel-plate capacitor is connected across a voltage V so that each plate of the capacitor collects a charge of magnitude Q. Which of the following is an expression for the energy stored in the capacitor?
(A)\(QV\)
(B)\(\frac{Q}{V}\)
(C)\(\frac{V}{Q}\)
(D)\(\frac{1}{2}QV\)
(E)\(\frac{1}{2}QV^2\)
Answer/Explanation
Ans:D
Question
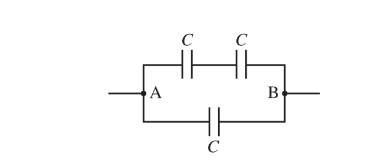
Three identical capacitors with capacitance C are arranged as shown above. What is the equivalent capacitance between points A and B?
(A) C /3
(B) 2C/3
(C) C
(D) 3C/2
(E) 3C
