Question
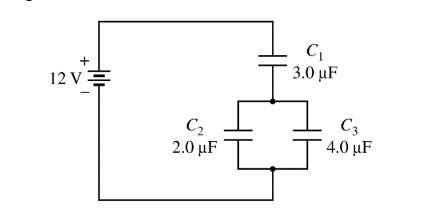
The circuit shown above has three capacitors and a 12 V battery. The capacitors are charged to steady state conditions.
One of the capacitors is removed from the circuit and isolated. While it still holds all of its charge, a piece of ceramic with dielectric constant of 2 is inserted and completely fills the space between the plates. \(U_i\) is the energy stored in the capacitor before the dielectric was inserted, and \(U_ f\) is the energy stored in the capacitor after the dielectricwas inserted. What is the ratio\( U_f/U_i\)?
(A) 14
(B) 12
(C) 11
(D) 21
(E) 41
Answer/Explanation
Question
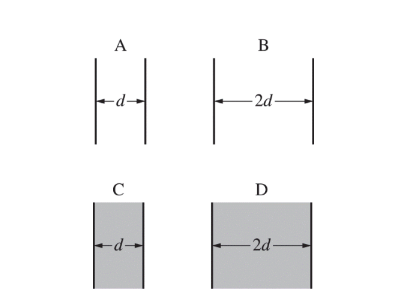
Four parallel plate capacitors all have the same plate area and have the plate separations shown above. Both capacitors A and B have air between the plates, while the space between the plates of both capacitors C and D is filled with a dielectric slab of dielectric constant κ = 2. Which of the following correctly ranks the capacitors in order of their capacitance from largest to smallest ?
(A)\( B > (A = D) > C\)
(E) \(D > C > B > A\)
Answer/Explanation
Ans:C

Question
A parallel plate capacitor is connected to a battery, fully charged, disconnected, and isolated from the battery. A dielectric slab is then inserted between the plates of the capacitor. Which of the following is a true statement about what happens when the dielectric slab is inserted?
(A) The magnitude of the electric field between the plates of the capacitor will increase.
(B) The potential difference between the plates of the capacitor will decrease.
(C) The capacitance of the capacitor will decrease.
(D) The charge stored on the capacitor will increase.
(E) The energy stored in the capacitor will increase.
Answer/Explanation
>Ans:B The parallel plate capacitor is connected to a battery to charge and then is isolated so the charge remains the same. Then, inserting a dielectric slab between the plates of the capacitor will
Question
The advantage of using a dielectric in a capacitor is that it
(A) increases the capacitance of the capacitor
(B) increases the conductivity of the capacitor
(C) decreases the charging time of the capacitor
(D) makes the capacitor dissipate less power
(E) eliminates the electric field in the capacitor
Answer/Explanation
Question
A dielectric of thickness \(\frac{d}{3}\) is placed between the plates of a parallel-plate capacitor, as shown above. If K is the dielectric constant of the slab, what is the capacitance?
(A) \(\frac{\varepsilon _{0}A(2+3K)}{d}\)
(B) \(\frac{d}{\varepsilon _{0}A(2+3K)}\)
(C) \(\frac{3\varepsilon _{0}A}{d(2K+1)}\)
(D) \(\frac{3K\varepsilon _{0}A}{d(2K+1)}\)
(E) \(\frac{3K\varepsilon _{0}A}{d}\)
Answer/Explanation
Ans: D
Treat the configuration as three capacitors in series, each with a distance between the plates of \(\frac{d}{3}\). The capacitance of the two vacuum capacitors will be \(\frac{\varepsilon _{0}A}{\frac{d}{3}}=\frac{3\varepsilon _{0}A}{d}\), and the capacitance of the dielectric capacitor will be that value times K. Now solve for the total capacitance for the three capacitors in series.
\(\frac{1}{C_{eq}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}\)
\(\frac{1}{C_{eq}}=\frac{1}{\frac{3\varepsilon _{0}A}{D}}+\frac{1}{\frac{3k\varepsilon _{0}A}{d}}+\frac{1}{\frac{3\varepsilon _{0}A}{d}}\)
\(\frac{1}{C_{eq}}=\frac{d}{3\varepsilon _{0}A}+\frac{d}{3K\varepsilon _{0}A}+\frac{d}{3\varepsilon _{0}A}\)
\(\frac{1}{C_{eq}}=\frac{2Kd+d}{3K\varepsilon _{0}A}\)
\(\frac{1}{C_{eq}}=\frac{3K\varepsilon _{0}A}{d(2K+1)}\)
Alternatively, this problem can be solved by process of elimination. First, use dimensional analysis. The Table of Information provided with the AP Test notes that capacitance should have units consistent with ε0 A / d; (B) fails this test. Second, pretend that the dielectric constant K = 1. This is the same as not having a dielectric, so plugging in K = 1 should give C = ε0
