Home / AP Physics C-Electricity and Magnetism -2025 – FRQ

Question 1

An isolated, air-filled, charged capacitor consists of two conducting, coaxial, cylindrical shells that each have length \(L\). The inner shell has radius \(R_{1}\) and the outer shell has radius \(R_{2}\), where \(R_{1} < R_{2} \ll L\). The surface charge densities of the inner and outer shells are \(+\sigma_{1}\) and \(-\sigma_{2}\), respectively. The absolute values of the total charges on the shells are equal.
(a)(i) Using Gauss’s law, derive an expression for the magnitude \(E\) of the electric field as a function of the radial distance \(r\) from the center of the capacitor for the region \(R_{1} < r < R_{2}\). Express your answer in terms of \(R_{1}\), \(\sigma_{1}\), \(r\), and physical constants, as appropriate.
(a)(ii) Derive an expression for the absolute value \(|\Delta V|\) of the potential difference between the outer and inner shells in terms of \(R_{1}\), \(R_{2}\), \(\sigma_{1}\), and physical constants, as appropriate. Begin your derivation by writing a fundamental physics principle or an equation from the reference information.
(a)(iii) On the axes provided, sketch a graph of \(E\) as a function of \(r\) from \(r=0\) to a position that is outside the outer shell.
 
(b) A material of dielectric constant \(\kappa\) is inserted into the isolated, charged capacitor such that the material fills the region \(R_{1} < r < R_{2}\). Derive an expression for the capacitance \(C\) of the capacitor with the material inserted in terms of \(L\), \(R_{1}\), \(R_{2}\), \(\kappa\), and physical constants, as appropriate.

Most-appropriate topic codes (CED):

• TOPIC 1.5: Gauss’s Law — part (a-i)
• TOPIC 2.1: Electric Potential — part (a-ii)
• TOPIC 2.3: Capacitance and Capacitors — part (a-iii, b)
• TOPIC 2.4: Dielectrics — part (b)
▶️ Answer/Explanation
Detailed solution

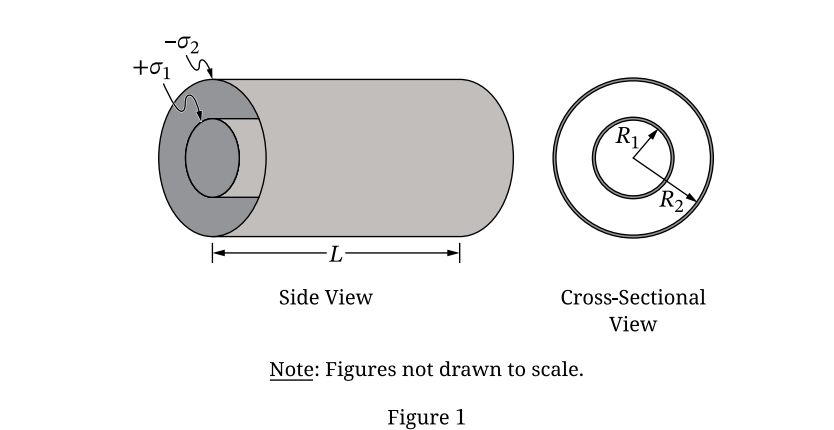
(a)(i)
Gauss’s Law: \(\oint \vec{E} \cdot d\vec{A} = \frac{q_{enc}}{\epsilon_{0}}\)
Gaussian surface: Cylinder of radius \(r\) and length \(l\).
\(E(2\pi rl) = \frac{\sigma_{1}(2\pi R_{1}l)}{\epsilon_{0}}\)
\(E = \frac{\sigma_{1}R_{1}}{\epsilon_{0}r}\)

(a)(ii)
Potential Difference: \(|\Delta V| = \left| -\int_{R_{1}}^{R_{2}} E \, dr \right|\)
\(|\Delta V| = \int_{R_{1}}^{R_{2}} \frac{\sigma_{1}R_{1}}{\epsilon_{0}r} \, dr = \frac{\sigma_{1}R_{1}}{\epsilon_{0}} [\ln r]_{R_{1}}^{R_{2}}\)
\(|\Delta V| = \frac{\sigma_{1}R_{1}}{\epsilon_{0}} \ln\left(\frac{R_{2}}{R_{1}}\right)\)

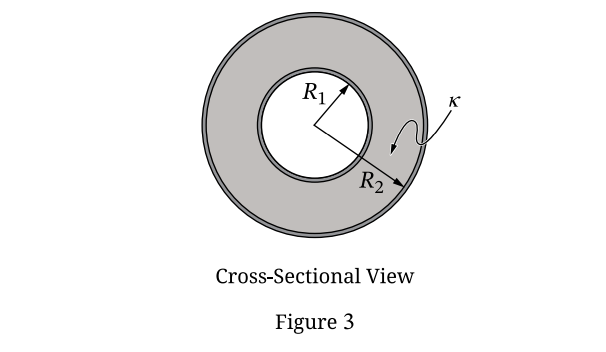
(a)(iii)
• \(0 < r < R_1\): \(E = 0\) (Inside conductor)
• \(R_1 < r < R_2\): \(E \propto \frac{1}{r}\) (Decreasing, concave up curve)
• \(r > R_2\): \(E = 0\) (Outside neutral capacitor)

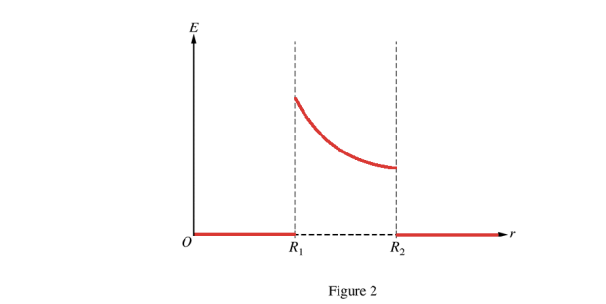
(b)
Capacitance definition: \(C = \frac{Q}{|\Delta V|}\) with dielectric \(\kappa\).
Total charge \(Q = \sigma_{1}(2\pi R_{1}L)\).
Potential with dielectric: \(|\Delta V|_{\kappa} = \frac{1}{\kappa} |\Delta V|_{air}\).
\(C = \frac{\sigma_{1} 2\pi R_{1} L}{\frac{1}{\kappa} \frac{\sigma_{1}R_{1}}{\epsilon_{0}} \ln(R_{2}/R_{1})} = \frac{2\pi \kappa \epsilon_{0} L}{\ln(R_{2}/R_{1})}\)

Question 2

A rotating, circular, conducting loop of area \(A\) and resistance \(R\) is in an external uniform magnetic field of magnitude \(B\) directed in the \(-z\)-direction. The loop rotates with constant angular speed \(\omega\) and period \(T\). The magnetic flux is given by \(\Phi = BA \cos(\omega t)\).
(a) The absolute value of the induced emf is \(|\mathcal{E}|\). A bar chart shows \(|\mathcal{E}|\) at \(t=\frac{3}{4}T\) (maximum). Draw bars to represent \(|\mathcal{E}|\) at times \(t=0\), \(\frac{1}{4}T\), and \(\frac{1}{2}T\).
(b) Derive an expression for the maximum induced current in the loop in terms of \(A\), \(R\), \(B\), \(\omega\), and physical constants. Begin your derivation by writing a fundamental physics principle.
(c) Sketch a graph of the instantaneous power \(P\) dissipated by the loop as a function of \(t\) during the interval \(0 \le t \le T\).
(d) Indicate whether the sketch in part (c) is consistent with the bars in part (a). Briefly justify your answer by referencing the functional dependence between \(P\) and \(|\mathcal{E}|\).

Most-appropriate topic codes (CED):

• TOPIC 13.2: Faraday’s Law and Lenz’s Law — part (a), (b)
• TOPIC 11.4: Resistivity and Resistance (Ohm’s Law/Power) — part (b), (c), (d)
▶️ Answer/Explanation
Detailed solution

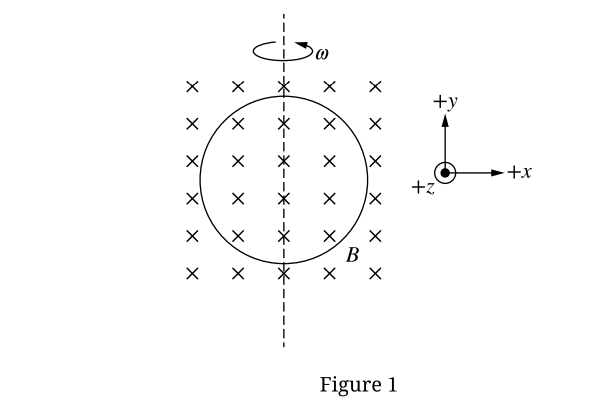
(a)
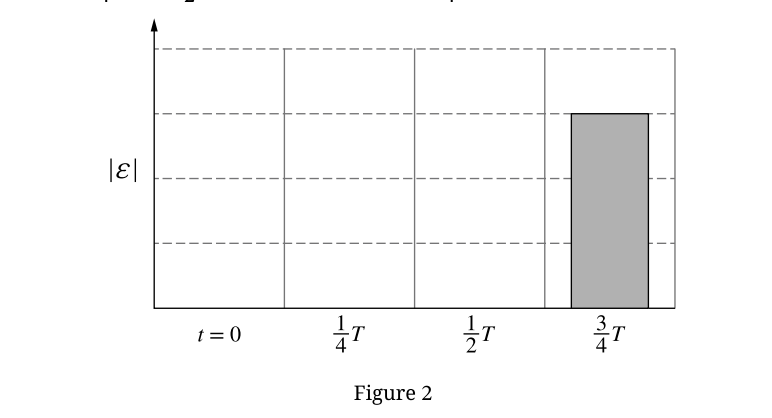
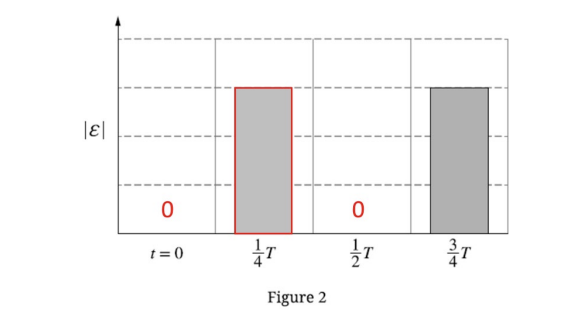
• \(t=0\): Height 0 (Flux is max, Rate of change is 0).
• \(t=\frac{1}{4}T\): Height equal to the bar at \(\frac{3}{4}T\) (Max EMF).
• \(t=\frac{1}{2}T\): Height 0.

(b)
Faraday’s Law: \(\mathcal{E} = -\frac{d\Phi}{dt}\)
\(\mathcal{E} = -\frac{d}{dt}(BA\cos(\omega t)) = -BA(-\omega\sin(\omega t)) = BA\omega\sin(\omega t)\)
Max EMF \(\mathcal{E}_{max} = BA\omega\)
Ohm’s Law: \(I_{max} = \frac{\mathcal{E}_{max}}{R} = \frac{BA\omega}{R}\)

(c)
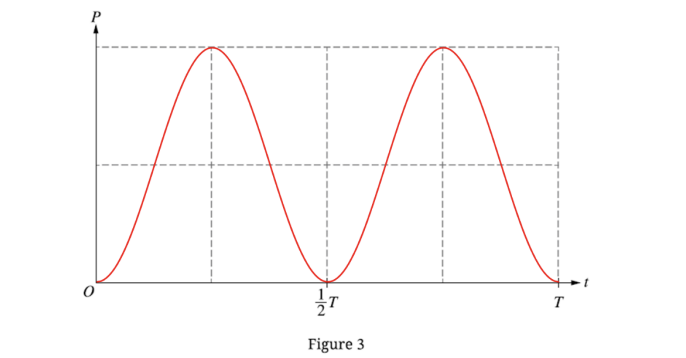
Sketch of \(P\) vs \(t\):
• Starts at \(0\) at \(t=0\).
• Peaks at \(t=\frac{1}{4}T\) and \(t=\frac{3}{4}T\).
• Zero at \(t=\frac{1}{2}T\) and \(t=T\).
• Shape is sinusoidal squared (always positive).

(d)
Consistent.
Relationship: \(P = \frac{\mathcal{E}^2}{R}\).
The power is proportional to the square of the emf. When emf is zero (at \(t=0, T/2\)), power is zero. When emf is maximum (at \(t=T/4, 3T/4\)), power is maximum. This matches the bars in (a) and the peaks in (c).

Question 3

Students are asked to use a graph to determine the resistivity \(\rho_{1}\) of a cylindrical circuit element using a variable power supply, voltmeter, ammeter, and ruler.
(a) Describe a procedure for collecting data to determine \(\rho_{1}\), including steps to reduce experimental uncertainty.
(b) Describe how the collected data could be graphed and analyzed to determine \(\rho_{1}\).
In Experiment 2, students determine the resistivity \(\rho_{2}\) of resistors with different lengths \(L\) but same cross-sectional area \(A = 5.0 \times 10^{-6} m^{2}\). The resistance \(R\) is measured for each.
(c) Indicate quantities to graph to produce a straight line to determine \(\rho_{2}\). Plot the data and draw a best-fit line.
(d) Using the best-fit line, calculate an experimental value for \(\rho_{2}\).

Most-appropriate topic codes (CED):

• TOPIC 11.3: Resistance, Resistivity, and Ohm’s Law — part (a), (b), (c), (d)
▶️ Answer/Explanation
Detailed solution

(a)
Procedure:
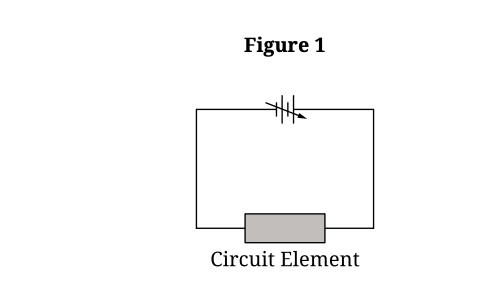
1. Measure the length \(L\) and diameter \(D\) of the cylinder using a ruler or calipers (to calculate Area \(A = \pi(D/2)^2\)).
2. Connect the cylinder in series with an ammeter and power supply, and connect a voltmeter in parallel with the cylinder.
3. Vary the voltage of the power supply to obtain at least 5 different pairs of voltage (\(\Delta V\)) and current (\(I\)) readings.

(b)
Analysis:
• Plot \(\Delta V\) on the vertical axis and \(I\) on the horizontal axis.
• Determine the slope of the best-fit line, which equals the resistance \(R\).
• Calculate resistivity using \(\rho_1 = \frac{R A}{L}\).

(c)
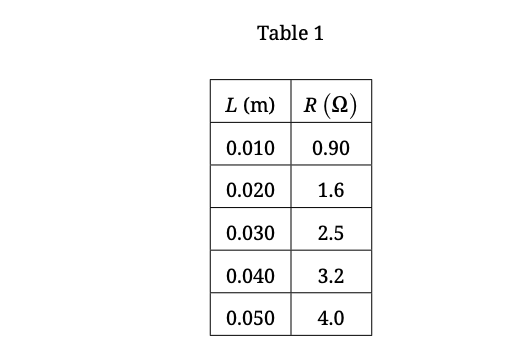
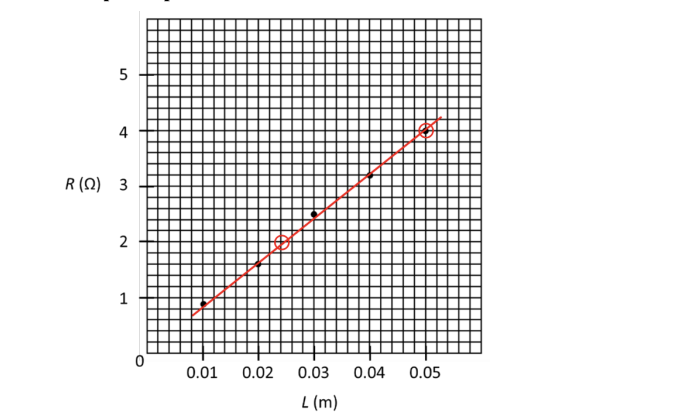
Graph Resistance \(R\) (Vertical) vs. Length \(L\) (Horizontal).
Since \(R = \frac{\rho_2}{A}L\), this plot yields a straight line through the origin.

(d)
Calculation:
• Calculate the slope of the best-fit line from the graph in (c): \(\text{Slope} = \frac{\Delta R}{\Delta L}\).
• Set \(\text{Slope} = \frac{\rho_2}{A}\).
• Solve for \(\rho_2 = \text{Slope} \times A\).
(Example: If Slope \(\approx 77 \, \Omega/m\), then \(\rho_2 \approx 77 \times 5.0 \times 10^{-6} \approx 3.9 \times 10^{-4} \, \Omega \cdot m\)).

Question 4

Long, parallel wires S and T are a distance \(2d\) apart carrying equal currents \(I\) in opposite directions. Sphere 1 (+Q) is distance \(d\) above Wire S. Sphere 2 (+Q) is distance \(d\) below Wire S (midway between wires). Both spheres move with speed \(v\).
(a) \(F_{1}\) is the magnetic force on Sphere 1. \(F_{2}\) is the magnetic force on Sphere 2. Indicate whether \(F_{2} > F_{1}\), \(F_{2} < F_{1}\), or \(F_{2} = F_{1}\). Justify your answer.
(b) Derive an expression for the magnitude \(B_{tot}\) of the magnetic field at the location of Sphere 2 in terms of \(d\), \(I\), and physical constants.
(c) Later, Wire T carries current \(3I\) in the \(+x\)-direction (same direction as Wire S). \(F_{new}\) is the new force on Sphere 2. Indicate whether \(F_{new} > F_{2}\), \(F_{new} < F_{2}\), or \(F_{new} = F_{2}\). Briefly justify your answer.

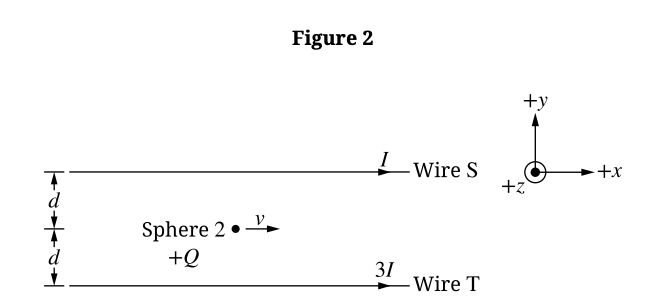
Most-appropriate topic codes (CED):

• TOPIC 4.4: Magnetic Field Created by Current-Carrying Wires — part (a), (b), (c)
• TOPIC 4.1: Forces on Moving Charges in Magnetic Fields — part (a), (c)
▶️ Answer/Explanation
Detailed solution

(a)
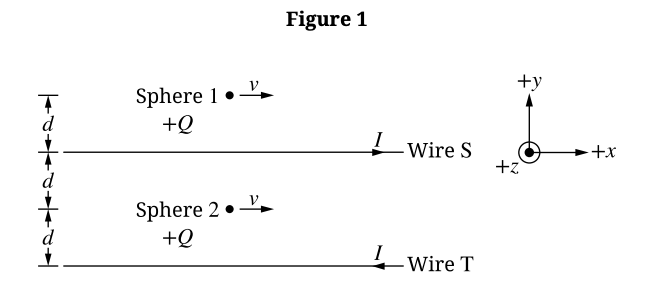
\(F_{2} > F_{1}\)
At Sphere 2 (between the wires), the magnetic fields from opposite currents point in the same direction and add constructively. At Sphere 1 (outside), the fields point in opposite directions and partially cancel. Since \(F \propto B\), the force is greater at Sphere 2.

(b)
Sphere 2 is distance \(d\) from Wire S and distance \(d\) from Wire T.
Field from a long wire: \(B = \frac{\mu_{0}I}{2\pi r}\).
Since fields add constructively:
\(B_{tot} = B_S + B_T = \frac{\mu_{0}I}{2\pi d} + \frac{\mu_{0}I}{2\pi d} = \frac{2\mu_{0}I}{2\pi d} = \frac{\mu_{0}I}{\pi d}\)

(c)
\(F_{new} = F_{2}\)
In the new scenario, the currents are in the same direction (\(+x\)), so the magnetic fields between the wires now oppose each other (subtract). Wire T has current \(3I\).
\(B_{new} = |B_{T,new} – B_S| = \frac{\mu_{0}(3I)}{2\pi d} – \frac{\mu_{0}I}{2\pi d} = \frac{2\mu_{0}I}{2\pi d} = \frac{\mu_{0}I}{\pi d}\)
The magnitude of the field (and thus the force) remains the same as in part (b).

Scroll to Top