Question
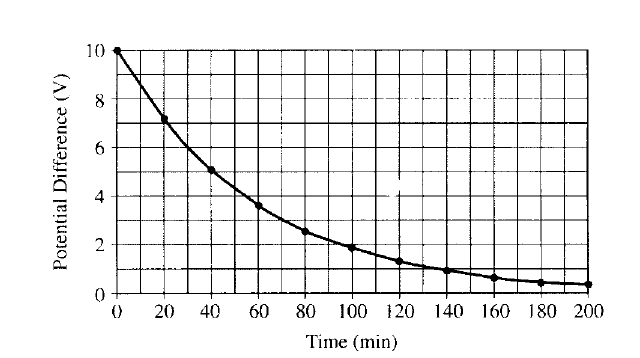
You have been hired to determine the internal resistance of 8.0 μF capacitors for an electronic
component manufacturer. (Ideal capacitors have an infinite internal resistance – that is, the material
between their plates is a perfect insulator. In practice, however, the material has a very small, but
nonzero, conductivity.) You cannot simply connect the capacitors to an ohmmeter, because their
resistance is too large for an ohmmeter to measure. Therefore you charge the capacitor to a potential
difference of 10 V with a battery, disconnect it from the battery and measure the potential difference
across the capacitor every 20 minutes with an ideal voltmeter, obtaining the graph shown above.
a. Determine the internal resistance of the capacitor.
The capacitor can be approximated as a parallel-plate capacitor separated by a 0.10 mm thick dielectric
with κ = 5.6.
b. Determine the approximate surface area of one of the capacitor “plates.”
c. Determine the resistivity of the dielectric.
d. Determine the magnitude of the charge leaving the positive plate of the capacitor in the first 100 min.
Answer/Explanation
Ans.
a. One method is to use the equation V = V0e–t/RC and substitute values from the graph,
e.g. V0 = 10 V, and V = 2 V at t = 100 min
2 = 10e(-6000 s)/R(8μF) giving R = 4.7 × 108Ω
b. C = κε0A/d so A = Cd/κε0 = 16 m2
c. R = ρL/A giving ρ = RA/L = 7.2 × 1013 Ω-m
d. One method is to use ΔQ = CΔV = (8 ×10–6 F)(10 V – 2 V) = 64 μC
Another method is to integrate I dt
