Question
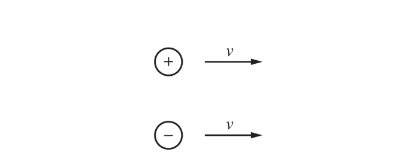
Two small spheres have equal and opposite charges and are travelling parallel to each other with speed v to the right, as shown above. What is the direction of the magnetic field midway between the spheres at the instant shown?
(A) Out of the page
(B) Into the page
(C) Toward the bottom of the page
(D) Toward the top of the page
(E) Undefined, since the magnitude of the magnetic field is zero.
Answer/Explanation
Question
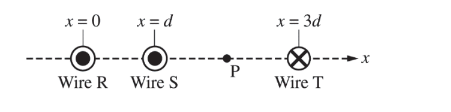
Three long, current-carrying wires are shown in the cross-sectional view above. The currents in wires R and S are out of the page, and the current in wire T is into the page. The currents in the wires have equal magnitude, and the wires are in the positions shown. Point P is halfway between wires S and T.
If \(B_S\) is the magnitude of the magnetic field at point P due to wire S, which of the following gives the magnitude and direction of the magnetic field at point P due to all three wires?
Magnitude Direction
(A) \(B_S/ 2 \) Top of the page
(B) \(B_S/ 2 \) Bottom of the page
(C) \(B_S\) Top of the page
(D) \(5B_S 2 \) Top of the page
(E) \(5B_S 2 \) Bottom of the page<
Answer/Explanation
Ans:D
Question
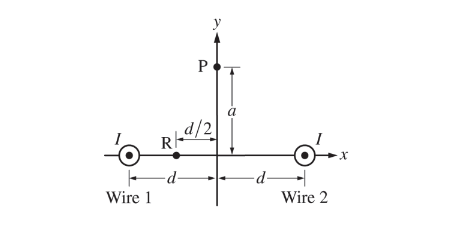
Two wires perpendicular to the x-axis have currents I directed out of the page, as shown above. Each wire is a distance d from the y-axis. Point P lies on the y-axis at the coordinate (0, a), and point R lies on the x-axis at the coordinate (−d/2, 0).
Which of the following expressions represents the magnitude of the magnetic field at point R?
(A) Zero
(B)\(\frac{\mu _{0}I}{2\pi d}\)
(C)\(\frac{\mu _{0}I}{\pi d}\)
(D)\(\frac{4\mu _{0}I}{3\pi d}\)
(E)\(\frac{2\mu _{0}I}{3\pi d}\)
Answer/Explanation
Question

Two wires perpendicular to the x-axis have currents I directed out of the page, as shown above. Each wire is a distance d from the y-axis. Point P lies on the y-axis at the coordinate (0, a), and point R lies on the x-axis at the coordinate (−d/2, 0).
Which of the following best represents the direction of the net magnetic field at point P?
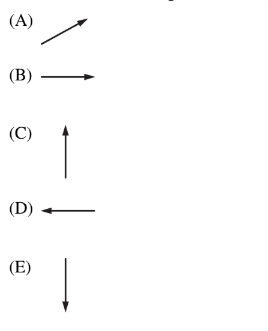
Answer/Explanation
Ans:D
Using the right-hand rule and drawing the circular magnetic field around the current carrying wire up to point P, the direction of the magnetic field due to wire 1 and wire 2 can be determined by taking the tangent vectors and adding them together. The magnetic field vector on point P due to wire 1 points upward and to the left. The magnetic field vector on point P due to wire 2
Question
A long, straight wire of radius R carries current I. he current is distributed over the cross-sectional aTrea of the wire with a uniform current density. Which of the following graphs best represents the magnetic field strength produced by the current as, a function of the distance r from the center of the wire?
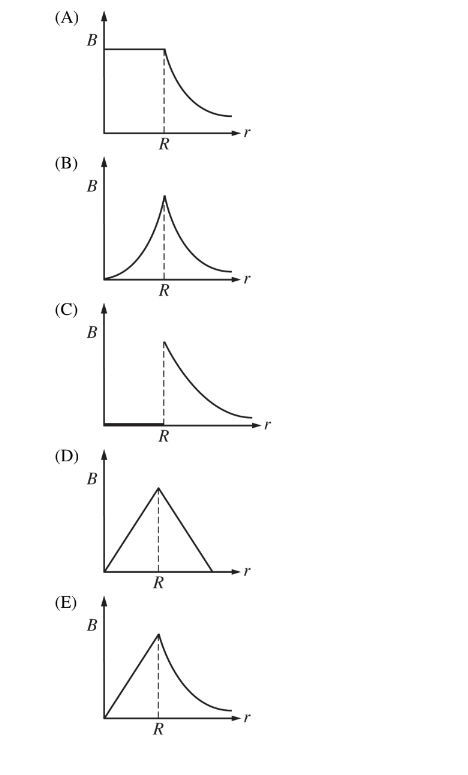
Answer/Explanation
Ans:E

