Question
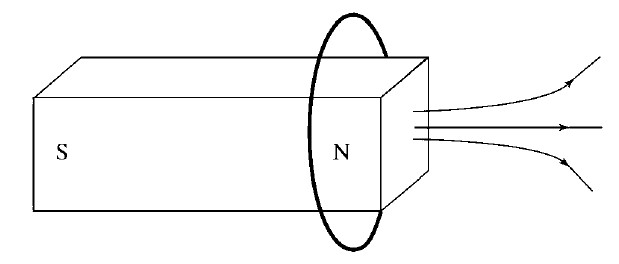
A conducting loop of wire is initially around a magnet as shown above. The magnet is moved to the left. What is the direction of the force on the loop and the direction of the magnetic field at the
center of the loop due to the induced current?
Direction of Force on Direction of Magnetic Field at Center of Loop
Loop Due to Induced Current
(A) To the right To the right
(B) To the right To the left
(C) To the left To the right
(D) To the left To the left
(E) No direction; To the left
the force is zero
Answer/Explanation
Ans: C
Question
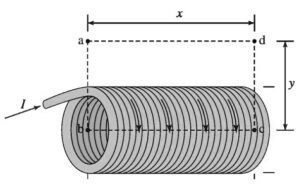
An ideal solenoid with N total turns has a current J passing through the helical wires that make up the solenoid. Ampere’s law is used with a rectangular path abed as shown above, to calculate the magnitude of the magnetic field B within the solenoid. The horizontal distances of the path are length x and the vertical distances of the path are length y. Which of the following equations results from the correct application of Ampere’s law in this situation?
(A) B(2x + 2y) = \(\mu _{o}NI\)
(B) B(2x) = \(\mu _{o}NI\)
(C) B(x + 2y) = \(\mu _{o}NI\)
(D) B(2y) = \(\mu _{o}NI\)
(E) B(x) = \(\mu _{o}NI\)
Answer/Explanation
Ans: E
Question
The figure above shows four current-carrying wires passing perpendicularly through the interior of a square whose vertices are W, X, Y, and Z. The points where the wires pierce the plane of the square (namely, R, S, T, and U) themselves form the vertices of a square each side of which has half the length of each side of WXYZ. If the currents are as labeled in the figure, what is the absolute value of \(\oint B.dl\) where the integral is taken around WXYZ?
(A) \(\frac{1}{2}\mu _{0}I\)
(B) \(\mu _{0}I\)
(C) \(\sqrt{2}\mu _{0}I\)
(D) \(2\mu _{0}I\)
(E) \(5\mu _{0}I\)
Answer/Explanation
Ans:D
Ampere’s law states that
\(\oint B.dl= \mu _{0}I_{net \ through\ loop}\)
Because a total current of 21 + 4,l = 61 passes through the interior of the loop in one direction, and a total current of I + 31 = 4,l passes through in the opposite direction, the net current passing through the loop is 61 – 4,l = 21. Therefore, the absolute value of the integral of B around the loop WXYZ is equal to µ0
Question
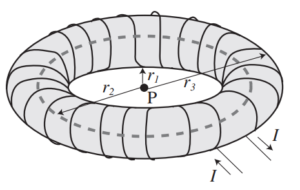
Wire is wound around an insulated circular donut, as shown above. A current I flows in the wire in the direction indicated by the arrows. The inner, average, and outer radii of the donut areindicated by \(r_1, r_2,\) and \(r_3\), respectively. What is the magnitude and direction of the magnetic field at point P, the center of the donut?
(A) zero
(B) \(\frac{\mu^{o}I}{2r_{1}}\)
(C) \(\frac{\mu^{o}I}{2r_{2}}\)
(D) \(\frac{\mu^{o}I}{2r_{3}}\)
(E) \(\frac{\mu^{o}I}{2\pi r_{2}}\)
Answer/Explanation
Ans:A
This is one of the important consequences of Ampère’s law. The magnetic field inside the donut is always along the axis of the donut, so the symmetry demands of Ampère’s law are met. If we draw an “Amperian Loop” around point P but inside r1
Question
A long straight wire of circular cross-section with radius a carries a uniform areal current density j. What is the value of the line integral of the magnetic field around the circumference of the wire?
(A) \(\mu _{0}j\pi a\)
(B) \(2\mu _{0}j\pi a\)
(C) \(2\mu _{0}j\pi a^{2}\)
(D) \(\mu _{0}j\)
(E) \(\mu _{0}j\pi a^{2}\)
Answer/Explanation
Ans: E
Ampere’s law says that the line integral of the magnetic field around a closed line is \(\mu _{0}I_{enclosed}\) How much current is enclosed by the circumference of the wire? The areal current density j times the area enclosed.The cross-sectional area enclosed here is just the area of the circular wire, πa2
