Question
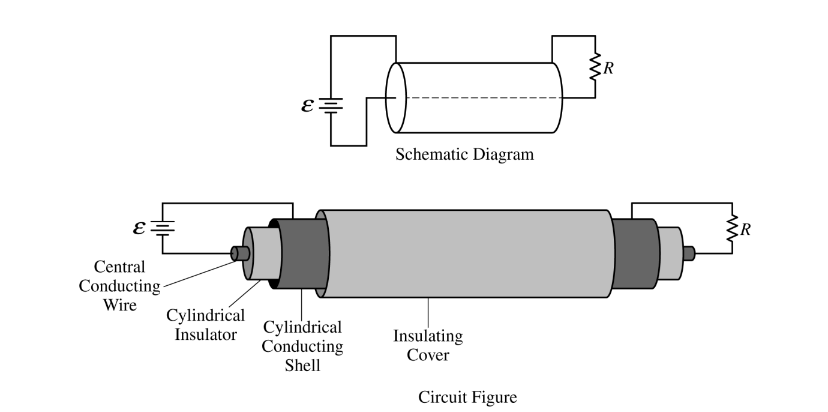
A coaxial cable is composed of a central conducting wire surrounded by a cylindrical insulator, and around that is a conducting cylindrical shell with an insulating cover. A power supply of emf ε is used at one end to connect the two conducting regions, and a resistive load of resistance R is connected at the other end of the cable to complete the circuit, as shown in the schematic diagram and circuit figure above.
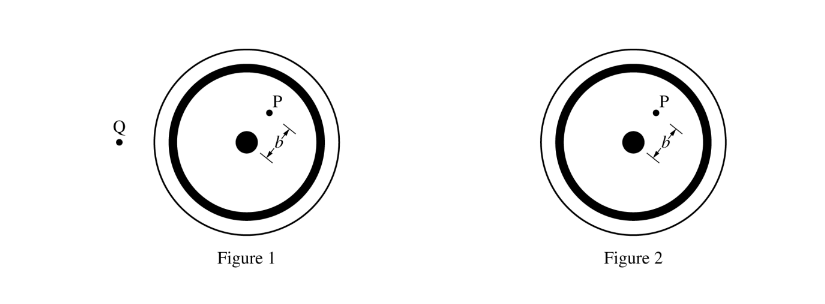
A cross section of the cable from the perspective of the power supply end is depicted above as if looking into the left end of the cable. Point P is inside the cylindrical insulator a distance b from the center of the cable. Point Q is outside the cable.
(a)
i. On figure 1 shown above left, draw an Amperian loop that could be used to determine the magnitude of the magnetic field at point P in the diagram. Clearly mark this loop as “Loop 1.”
ii. On figure 1, draw an Amperian loop that could be used to determine the magnitude of the magnetic field at point Q in the diagram. Clearly mark this loop as “Loop 2.”
iii. On figure 2 shown above right, draw an arrow to show the direction of the magnetic field at point P. The arrow should start on and point away from the point in the direction of the magnetic field.
(b) Using Ampere’s law, derive an expression for the magnitude of the magnetic field at point P. Express your answer in terms of ε , R, b, and physical constants, as appropriate.
(c) Determine the magnitude of the magnetic field at point Q.Some physics students conduct an experiment with a coaxial cable in which they connect the cable to a variable power supply and measure the resulting magnetic field strength at point P inside the cylindrical insulator using a magnetic field sensor. Point P is 0.0050 m from the center of the cable. The plot of the magnetic field strength B as a function of the emf ε of the power supply is shown below.
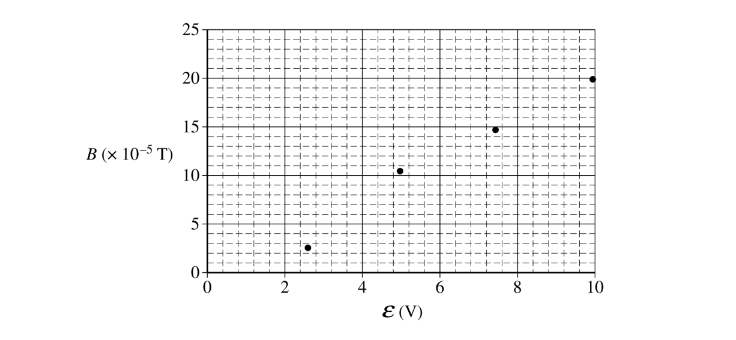
(d)
i. Draw the best-fit line for the data.
ii. Use the straight line to calculate the resistance R of the resistor used in the experiment.
(e) The lab group uses a multimeter to measure the resist ance of the resistor and determines that their experimental value for R from part (d) is approximately 10% larger than that found with the multimeter. Describe a physical reason that might account for this result.
(f) The lab group notices that when the current is reversed in the cable and the experiment is again performed, the plot has a positive vertical axis intercept equal in magnitude to the negative vertical axis intercept in the plot shown before part (d).
i. Describe a physical reason for the vertical axis intercept.
ii. Describe a physical reason that the vertical axis intercept switches from negative to positive when the current in the cable is reversed.
Answer/Explanation
Ans:
(i) For properly drawing and labeling a circle concentric with the other circles and through
ii) For properly drawing and labeling a circle concentric with the other circles and through
point Q
(a)iii) For properly drawing a straight arrow at point P that indicates the magnetic field is tangent to Loop 1 from part (a)(i) For indicating a counter-clockwise magnetic field around Loop 1 from part (a)(i)
(b) For using Ampere’s law at point P \(\oint \vec{B}d\vec{l}=\mu _{0}I\) For correctly substituting for § di В(2лb) = \mu _{0}I\) For correctly substituting for I В(2лb) = \mu _{0}\)\frac{ε}{R} \therefore B=\(\frac{\mu _{0}\varepsilon }{2 \pi b R}\)
(c) For indictaing that the magnetic field at point Q is zero For a correct justification Example: Since Loop 2 encloses both the inside wire and the outer conducting shell and the two of them have equal and opposite currents, the net enclosed current is zero. Thus the magnetic field at point Q is zero.
(d)
i) For properly drawing a trend line on the graph
ii) For correctly calculating the slope from the best-fit line and not the data points
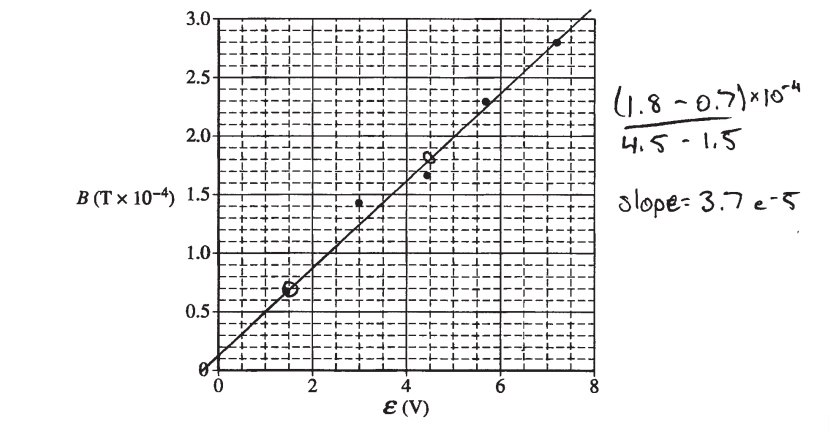
\(slope=\frac{\Delta B}{\Delta \varepsilon }=\frac{(20-5)(T\times 10^{-5})}{(9.4-3.2)(V)}=2.42\times 10^{-5}T/V\)
For correctly relating the slope to the equation from part (b)
\(slope=\frac{\mu _{0}}{2\pi bR}\therefore \frac{\mu _{0}}{slope\times 2 \pi b}=\frac{4 \ pi\times 10^{-7}T.m/A}{(2.42\times 10^{-5}T/V)(2\pi)(0.0050m)}\) \( 1.65
\Omega \)
(e) For an appropriate explanation for the difference in the resistance values Example: There is resistance in the wires, thereby increasing the total experimental resistance.
(f) i) For an appropriate explanation for the vertical axis intercept Example: The magnetic field sensor was not zeroed at the start of the experiment to account for the Earth’s magnetic field
ii) For an appropriate explanation for the intercept switching from negative to positive Example: When the current is reversed, the cable’s magnetic field switches direction but the external magnetic field from the Earth remains constant.
Question
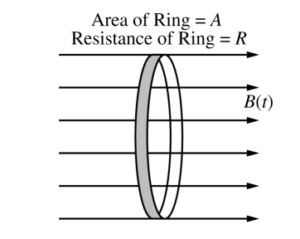
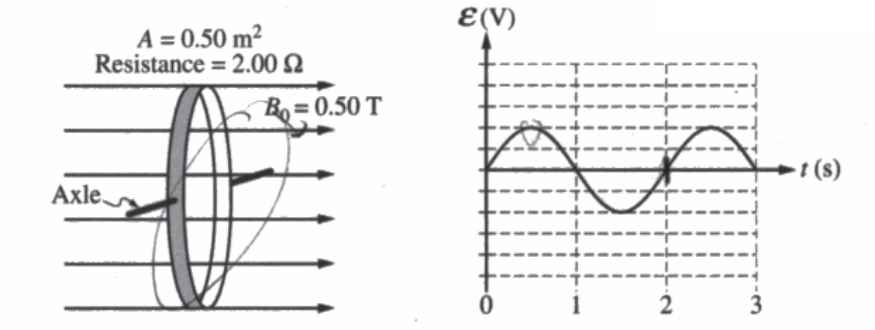
A thin, conducting ring of area A and resistance R is aligned in a uniform magnetic field directed to the right and perpendicular to the plane of the ring, as shown. At time t = 0, the magnitude of the magnetic field is B0. At t = 1 s, the magnitude of the magnetic field begins to decrease according to the equation \(B(t)=\frac{\beta }{t}\) , where β has units of T · s.
(a) Derive an equation for the magnitude of the induced current I in the ring as a function of t for t > 1 s.
Express your answer in terms of β, A, R, t, and physical constants, as appropriate.
Assume A = 0.50 m2, R = 2.0 Ω, and β = 0.50 T · s.
(b) Calculate the electrical energy dissipated in the ring from t = 1 s to t = 2 s.
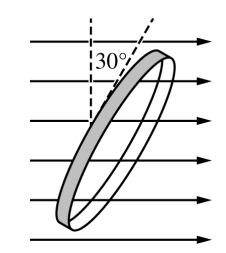
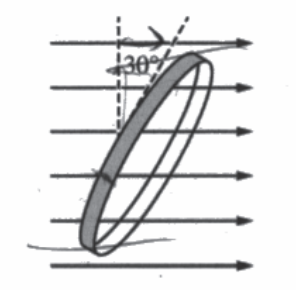
The ring is then rotated so that the plane of the ring is aligned at a 30° angle to the magnetic field, as shown. The magnitude of the magnetic field is reset to a magnitude of B0 at a new time t = 0 and again begins to decrease at t = 1 s according to the equation \(B(t)=\frac{\beta }{t}\) , where β has units of T · s.
(c) Will the amount of energy dissipated in the ring from t = 1 s to t = 2 s be greater than, less than, or equal to the energy dissipated in part (b) ?
_____ Greater than _____ Less than _____ Equal to
Justify your answer.
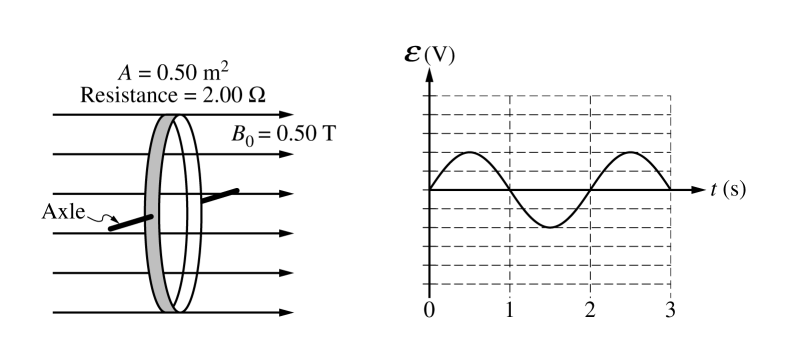
The ring is now mounted on an axle that is perpendicular to the magnetic field. The magnitude of the magnetic field is now held at a constant B0 = 0.50 T, as shown. The ring rotates about the axle, and the emf ε induced in the ring as a function of time t is shown on the graph.
(d) Calculate the angular speed ω of the rotating ring in rad/s.
(e) Calculate the magnitude of the maximum emf εMAX induced in the ring.
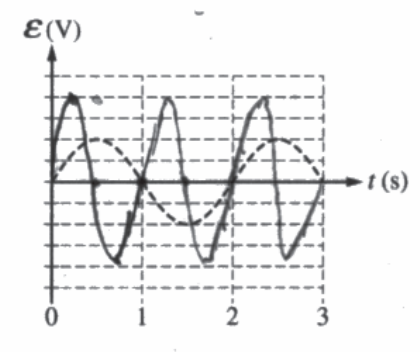
The ring now begins to rotate at an angular speed 2ω.
(f) On the graph below, draw a curve to indicate the new induced emf ε in the ring. The dashed curve shows the emf induced under the original conditions.
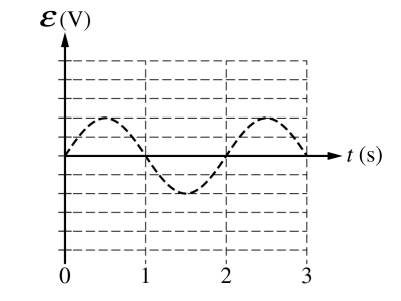
Justify your sketch, specifically identifying and addressing any similarities or differences between the sketch and the original graph.
Answer/Explanation
Ans:
(a)
\(\left | \varepsilon \right |=\left | \frac{dI_{B}}{dt} \right |= \left | \frac{d}{dt} (SB\cdot dA)\right |=\left | \frac{d}{dt} BA\right |=\left | A\frac{dB}{dt} \right |=\left | -A\frac{B}{t^{2}} \right |=\left | A\frac{\beta }{t^{2}} \right |\)
\(\varepsilon /R = i \Rightarrow \frac{A\beta }{Rt^{2}}\)
(b) P = I2R = electrical energy dissipated \(\int P dt = \int I^{2}R dt\)
\(=\int \frac{A^{2}\beta ^{2}}{Rt^{4}}dt\)
0.121 J \(\Leftarrow \frac{(0.5)^{2}(0.5)^{2}}{2}\left ( \frac{4}{1}-\frac{4}{32} \right )\) \(\frac{A^{2}B^{2}}{R}\int_{t=1}^{t=2}\frac{1}{t^{4}}dt\)
\(P = \left ( \frac{AB}{Rt^{2}} \right )R=\frac{A^{2}B^{2}}{Rt^{4}}\) \(\frac{A^{2}B^{2}}{R}\left ( \frac{-4}{t^{5}} \right )_{1}^{2}\)
(c)
√ Less than
Now only a portion of the saw magnetic field (Bit) sin(30), to be exact) does through the loop. This decreases the EMF, the current, and thus the power dissipate.
(d)
Period T = 2s as per 2nd graph \(w = \frac{2\pi radius}{2s}=\pi \frac{rod}{sec}\)
(e)
\(\varepsilon = \frac{dI_{b}}{dt}\cdot B\frac{dA}{dt}\) A = A cos (wt)
\(\frac{dA}{dt}=-Asin(wt) (w)\)
ε = BA w sin (wt) wt = π/2
0.185 v = (0.5) (0.5)(π)(1) = π/4 t = 1/2
w = π
(f)
ε = BA ws, hurt
The period will now be solved
The amplitude will double because ε ∝ w. This makes serve because the area will be changing more rapidly, so a greater Emf will be induced.
Question
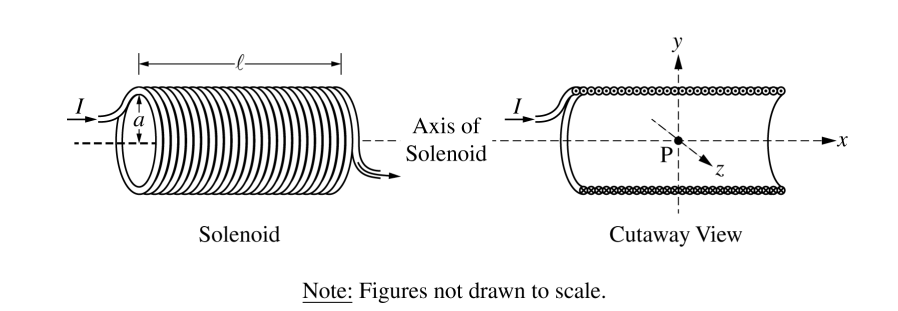
A solenoid is used to generate a magnetic field. The solenoid has an inner radius a, length l , and N total turns of wire. A power supply, not shown, is connected to the solenoid and generates current I, as shown in the figure on the left above. The x-axis runs along the axis of the solenoid. Point P is in the middle of the solenoid at the origin of the xyz-coordinate system, as shown in the cutaway view on the right above. Assume l >> a .
(a) Select the correct direction of the magnetic field at point P.
____ +x-direction ____ +y-direction ____ +z-direction
____ –x-direction ____ –y-direction ____ –z-direction
Justify your selection.
(b)
i. On the cutaway view below, clearly draw an Amperian loop that can be used to determine the magnetic field at point P at the center of the solenoid.
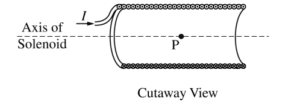
ii. Use Ampere’s law to derive an expression for the magnetic field strength at point P. Express your answer in terms of I, l, N, a, and physical constants, as appropriate.
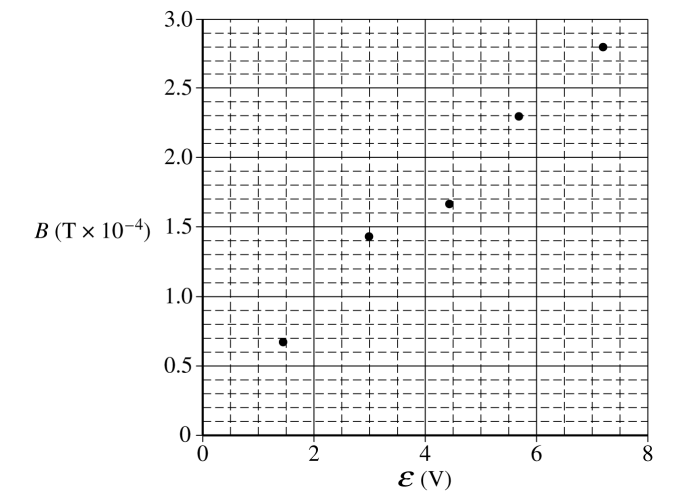
Some physics students conduct an experiment to determine the resistance RS of a solenoid with radius a = 0.015 m, total turns N = 100, and total length l = 0.40 m. The students connect the solenoid to a variable power supply. A magnetic field sensor is used to measure the magnetic field strength along the central axis at the center of the solenoid. The plot of the magnetic field strength B as a function of the emf ε of the power supply is shown below.
(c)
i. On the graph above, draw a best-fit line for the data.
ii. Use the straight line to determine the resistance RS of the solenoid used in the experiment.
(d) One of the students notes that the horizontal component of the magnetic field of Earth is 2.5 × 10-5 T .
i. Is there evidence from the graph that the horizontal orientation of the solenoid affects the measured values for B ?
____ Yes ____ No
Justify your answer.
ii. Would the horizontal orientation of the solenoid affect the calculated value for RS ?
____ Yes ____ No
Justify your answer
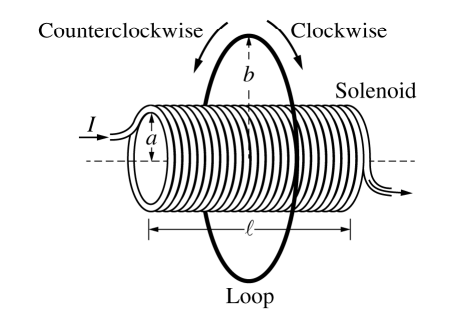
A thin conducting loop of radius b and resistance RL is placed concentric with the solenoid, as shown above. The current in the solenoid is decreased from I to zero over time Δt.
(e)
i. Is the direction of the induced current in the loop clockwise or counterclockwise during the time period that the current in the solenoid is decreasing?
____ Clockwise ____ Counterclockwise
Justify your answer.
ii. Derive an equation for the average induced current iIND in the loop during the time period that the current in the solenoid is decreasing. Express your answer in terms of I, l, N, a, b, RL , RS , Δt, and physical constants, as appropriate.
Answer/Explanation
Ans:
(a) Using the right hand rule, curl your fingers in the direction of the current, thumb points in the direction of \(\overrightarrow{B}\) field
(b) i. 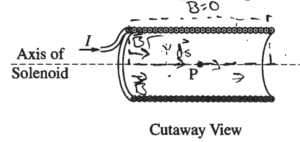
ii.
\(\int \overrightarrow{B}\cdot d\overrightarrow{s}=M_{0}I\) N = number of turns
\(\int \overrightarrow{B}\cdot d\overrightarrow{s}=M_{0}NI\) only place θ = 0 is
along axis of solnoid
\(\int B cos\theta ds = M_{0}NI\)
\(\int B ds = M_{0}NI\)
Bl = M0NI
\(B_{s} = \frac{M_{0}NI}{l}\)
(c) i.
ii.
\(B_{s} = \frac{M_{0}NI}{l}=\frac{M_{0}NV}{lR}\) Bvs.V \(slope=\frac{M_{0}N}{lR}\)
\(R=\frac{M_{0}N}{l(slope)}\)
\(R=\frac{\left ( 4\pi \times 10^{-7}(100) \right )}{(.40)(3.7-5)}=8.5 \mu \)
(d)
i. __X___ Yes
The best fit line will not have a y-intercept of zero. The y-intercept will be 2.5 × 10-5 T
ii. __X___ No
The y-intercept of the graph has no effect on the slope
(e)
i. __X___ Clockwise
According to Lenz’s Law. a decreasing field to the right will induce a field in the same direction in order to maintain \(\frac{d\Phi }{d_{4}}net = 0\)
ii.
\(\sum = \frac{\Delta \Phi }{\Delta t} = \frac{\Delta (BA) }{\Delta t}=A\frac{\Delta \left ( M_{0} \frac{N}{l}I\right ) }{\Delta t}=\frac{AM_{0}N}{l} \frac{\Delta I}{\Delta l}\)
\(I=\frac{\varepsilon }{R}=\frac{AM_{0}N}{R_{L}l} \frac{\Delta I}{\Delta l}=\frac{(\pi a^{2})M_{0}N}{R_{L}l}\left ( \frac{\Delta I}{\Delta t} \right )\)
