Question
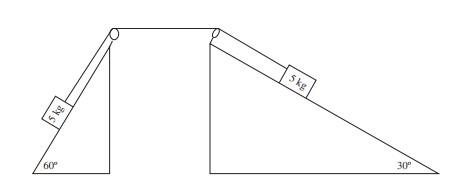
Two 5-kg masses are connected by a light string over two massless, frictionless pulleys. Each block sits on a frictionless inclined plane, as shown above. The blocks are released from rest.
(a) Determine the magnitude of the acceleration of the blocks. Now assume that the \(30^{\circ}\) incline provides a resistive force which depends on speed v. This resistive force causes the entire system’s acceleration to be given by the expression a = 1.8 − 0.03v where a speed v in m/s gives an acceleration in m/\(s^{2}\). The blocks are again released from rest.
(b) i. On the axes below, sketch a graph of the speed of the 5 kg block as a function of time. Label important values, including any asymptotes and intercepts.

ii. Explain how the expression for acceleration leads to the graph you drew.
(c) Explain how to figure out the terminal speed of the 5 kg block.
(d) The terminal speed is 60 m/s – that’s a typical speed in automobile racing. Explain briefly why this result is physically reasonable, even though the blocks are on a track in a physics laboratory.
Answer/Explanation
Ans:
(a) 1 pt: Write Newton’s second law for the direction along the plane for each block. For the right block, T − mg sin 30° = ma For the left block mg sin 60° − T = ma
1 pt: for including consistent directions for both equations
1 pt: for including a trig function in both equations, even if it’s the wrong function
1 pt: solve these equations simultaneously to get the acceleration
1 pt: answer is a = 1.8 m/\(s^{2}\). (An answer of a =−1.8 m/\(s^{2}\) is incorrect because the magnitude of a vector cannot be negative.) (Alternatively you can just recognize that mg sin 60° pulls left, while mg sin 30° pulls right, and use Newton’s second law directly on the combined system. Be careful, though, because the mass of the ENTIRE system is 10 kg, not 5 kg!)
(b) i. 
1 pt: for a graph that starts at v = 0, has exponential form, and sort of levels off to a maximum speed.
1 pt: for indicating that the asymptote represents the terminal speed, or 60 m/s.
ii. 1 pt: since acceleration is dv/dt, we have a differential equation: dv/dt = 1.8 − 0.03v. We need to find the expression for v.
1 pt: In a differential equation where the derivative is proportional to the function itself, the solution has an exponential term.
1 pt: In the solution e is raised to the −0.03t power because 0.03 is what multiplies the v.
1 pt: Since the blocks start at rest and speed up, the solution includes \((1-e^{-0.03})\) not just \(e^{-0.03t}\). [Those previous three points could be earned for a direct algorithmic solution for v, using separation of variables and integration.]
1 pt: For large t, the exponential term goes to zero, and so \((1-e^{-0.03t})\) should be multiplied by the terminal velocity. That’s why there’s an asymptote.
(c) 1 pt: The terminal velocity is when acceleration equals zero.
1 pt: solve the equation 0 = 1.8 − 0.03v. (You get 60 m/s.)
(d) 1 pt: The blocks only reach this terminal speed after a long time. An incline in a physics lab can’t be more than a couple of meters long, meaning the blocks don’t have the time and space to reach 60 m/s.
Question
An ideal projectile is launched from the ground at an angle \(\theta \) to the horizontal, with an initial speed of \(v_o,\) The ground is flat and level everywhere. Write all answers in terms of \(v_o, \theta \),
and fundamental constants.
(a) Calculate the time the object is in the air.
(b) Calculate the maximum height the object reaches.
(c) What is the net vertical displacement of the object?
(d) Calculate the range (horizontal displacement) of the
object.
(e) What should \(\theta\) be so that the projectile’s range is equal to
its maximum vertical displacement?
Answer/Explanation
This problem involves motion in two dimensions, so it’s important to begin by drawing a large picture of the situation. Note that our coordinate system is set up in the usual way with
x pointing to the right, y pointing up, and the origin at the point where the projectile is launched.
Next, draw a second diagram that splits \(\overheadarrow{v} _o \) into vertical and horizontal components. Note that you can use trigonometric properties to derive the values of \(v_{ox}\) and \(v_{oy}\).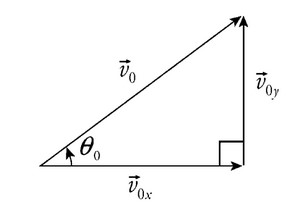
Now we’re ready to start answering the questions.
(a) For this problem, time of flight is determined by vertical quantities. This is because the flight ends when the object hits the ground, that is, when the y-coordinate is zero again.
If ~y = o, the projectile is either beginning or ending its flight.
You need to find t and you’re missing \(v_{f,y}\), so use Big Five #3.
\(\Delta y = v_{o,y}t + \frac{1}{2} a_u t^2\)
\(o = (v_o sin \theta) t + \frac{1}{2} (-g)t^2\)
\(\frac{1}{2} gt^2 – (v_o sin \theta) t =0\)
\(t(\frac{g}{2} t – v_o sin \theta ) = 0\)
At the beginning of the flight, t is equal to o. However, at the end of the flight, you would have the following:
\(\frac{g}{2} t – v_o sin \theta = 0\)
\(\frac{g}{2} t = v_o sin \theta \)
\(t = (\frac{2v_o sin \theta}{g})\)
The total amount of time in the air, then, is \((\frac{2v_0 sin \theta}{g}) – 0\), or just \((\frac{2v_o sin \theta}{g})\).
As an alternative, you could use Big Five # 2 to find the amount of time in which the projectile moves upward and then multiply that number by 2 to get the total time.
(b) As with the previous step, you are looking for a vertical quantity; because it’s t that you no longer care about and dy that you need, use Big Five # 5.
\(v_{fy}^2 = v_{oy}^2 + 2a (\Delta y)\)
At the top of the trajectory, \(v_{fy}=0\), which means you can now solve for \(\Delta y\).
\(o = v_{ou}^2 + 2a \Delta y\)
\(-v_{oy}^2 = 2a \Delta y\)
\(\frac{-v_{oy}^2}{2a}= \Delta y\)
If you plug in the known values of \(v_{oy}\) and a, you get the following:
\(\Delta y = \frac{-(v_o sin \theta )^2}{2(-g)}\)
\(\Delta y = \frac{v_0^2 sin^2 \theta}{2g}\)
Because \(u_o=0\), that value of \(\Delta y\) is also the value of \(y_{max}\)
(c) The object starts and ends on the ground (y = o), so its net
vertical displacement is o.
(d) You’re asked for a horizontal quantity, so let’s review our horizontal components.
\(\Delta x = ?\)
\(v_x = v_o cos \theta \)
\(t = \frac{2v_o sin \theta}{g}\)
Velocity is defined as \(v_x = \frac{\Delta x}{t}\), and this can be rewritten as \(\Delta x = v_x t\). You’ve found two of these values already, so plug them in and solve.
\(\Delta x = (v_o cos \theta ) (\frac{2v_0 sin \theta}{g})\)
\(\Delta x = \frac{2v_0^2 sin \theta cos \theta}{g}\)
(e) We’re told that the range equals the maximum vertical displacement, so \(\Delta x = y_{max}\)
\(\frac{2v_0^2 sin \theta cos \theta}{g} = \frac{v_o^2 sin^2 \theta}{2g}\)
Cancelling out form this equation, you’re left with the following:
\(2 cos \theta = \frac{sin \theta}{2}\)
\(4 = tan \theta\)
\(\theta = tan^{-1}(4)\)
You can check this by noting that the arctan of 4 is a fairly large angle (about 76°), which indicates that \(\overheadarrow{v}_0\) points more upward than rightward.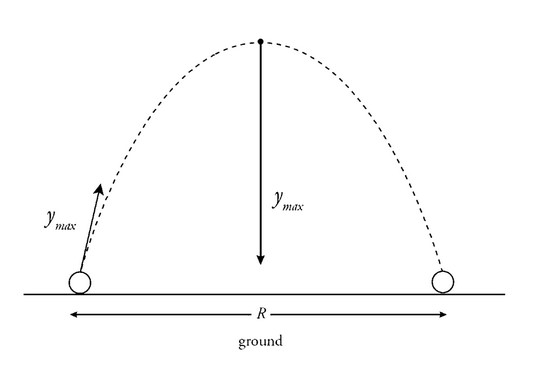
Question
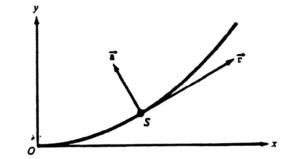
A particle moves along the parabola with equation y = \(\frac{1}{2}\) x2
a. Suppose the particle moves so that the x-component of its velocity has the constant value vx = C; that is, x = Ct
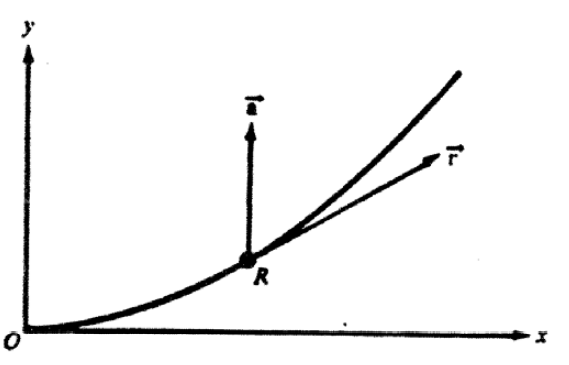
i. On the diagram above, indicate the directions of the particle’s velocity vector v and acceleration vector a at point R, and label each vector.
ii. Determine the y-component of the particle’s velocity as a function of x.
iii. Determine the y-component of the particle’s acceleration.
b. Suppose, instead, that the particle moves along the same parabola with a velocity whose x-component is given by vx = C/(1+x²)½
i. Show that the particle’s speed is constant in this case.
ii. On the diagram below, indicate the directions of the particle’s velocity vector v and acceleration vector a at point S, and label each vector. State the reasons for your choices.
Answer/Explanation
Ans:
a) i. The velocity vector is tangent to the path. Since vx is constant, ax = 0, and the acceleration vector has only a positive y component.
ii. The y component of the velocity is vy since y = ½ x = dy/dt, and by the chain rule dy/dt = (dy/dx)(dx/dt) since y = 1/2 x2 , dy/dt = x and vy = x(dx/dt) = Cx
iii. The acceleration is given by ay = dvy/dt, so ay = C(dx/dt) = C2
b) i. The speed is given by 𝑣 = \(\sqrt{{v_{x}}^{2}+{v_{y}}^{2}}\), by the chain rule, vy = dy/dt = (dy/dx)(dx/dt) = xvx
so 𝑣 = \(\sqrt{{v_{x}}^{2}\left ( 1+x^{2} \right )} = \sqrt{\frac{c^{2}}{1+x^{2}}\left ( 1+x^{2} \right )} = C\)
ii. Again the velocity vector is tangent to the path, but since the speed is constant, there is no component of the acceleration along the path, so a is centripetal, perpendicular to v