Question

A block of mass m is placed on top of an ideal spring of spring constant k . The block is pushed against the spring, compressing the spring a distance ∆x. The block is released from rest, leaves the spring at the position shown in the figure, travels upward, and enters a track with a constant radius of curvature R that has negligible friction. The block enters the track at point A, maintains contact with the track, and exits horizontally at point B, a distance 3R above the point the block was released. The block then falls to the ground and lands a horizontal distance D from the end of the track. Express all algebraic answers in terms of m, k , , ∆x R, and physical constants, as appropriate. The size of the block is much smaller than the radius of curvature of the track.
(a) On the dot below, which represents the block, draw and label the forces (not components) that act on the block while still in contact with the track at point B. Each force must be represented by a distinct arrow starting on, and pointing away from, the dot.
Justify your choice of vectors.
(b)
i. Derive an expression for the speed v of the block at point B.
ii. Derive an expression for the magnitude of the net force F on the block at point B.
(c) Derive an expression for the minimum value of Δxmin required in order for the block to maintain contact with the track through point B. The procedure is repeated several times with the distance Δx > Δxmin.
(d) Calculate the distance D that the block travels.
(e) The graph below shows the best-fit line drawn by the students through their data of D as a function of Δx.
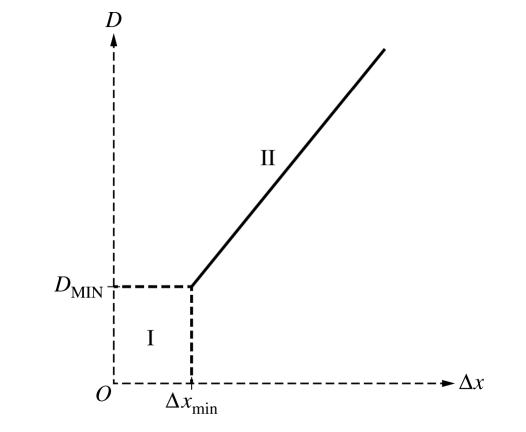
i. Explain why there are no data for section I of the graph.
ii. Explain the reason for the shape and minimum value of section II on the graph.
Answer/Explanation
Ans:
(a)
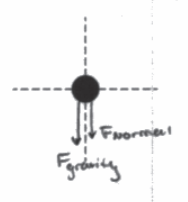
The force of gravity is includes because it always polls objects toward the earth (down). Depending on how fast the block is moving, it might also experience a normal force from the ramp. The normal force is always perpendicular to the surface, so it too points down
(b)
i.
E2 = E1
Kf + Uf = Usil
\(\frac{1}{2}mv^{2}+mgh = \frac{1}{2}ux^{2}\)
\(mv^{2}+2mg(3R)=k(\Delta x)^{2}\)
\(v = \sqrt{\frac{k(\Delta x^{2})-comgR}{m}}\)
ii.
\(F_{net}=\frac{mv^{2}}{R}\)
\(=\frac{m\left ( \frac{k(\Delta x)^{2}-6 mg R}{m} \right )}{R}\)
\(F = \frac{k(\Delta x)^{2}}{R}-6mg\)
(c)
\(F_{grav}=\frac{mv^{2}}{r}\)
\(mg=\frac{mv^{2}}{R}\)
\(v = \sqrt{gR}\)
\(\sqrt{gR}=\sqrt{\frac{k(\Delta x^{2})-6 mgR}{m}}\)
mgR = k(Δx)2 – 6mgR
7mgR = k(Δx)2
\(\Delta x_{min} = \sqrt{\frac{7mgR}{k}}\)
(d)
\(w/f_{f}=y_{1}+{v_{1}}^{t}+\frac{1}{2}at\)
\(0 = 3R – \frac{(g)}{2}t^{2}\)
\(\sqrt{\frac{6R}{g}}= t\)
xf = x1 + vt
D = v(t)
\(D = \sqrt{\frac{k(\Delta x)^{2}-6mgR}{m}}.\sqrt{\frac{6R}{g}}\)
\(D = \sqrt{\frac{6kR(\Delta x)^{2}-6mgR^{2}}{mg}}\)
(e)
i.
When Δx is less than Δxmin, the block does not maintain contact with the track until point B
ii.
D is directly proportional to the square root of (Δx)2, which means that D is proportional to Δx, this linear relationship produces a line.
Question
A toy rocket of mass 0.50 kg starts from rest on the ground and is launched upward, experiencing a vertical net force. The rocket’s upward acceleration a for the first 6 seconds is given by the equation a = K- Lt2 , where K = 9.0 m/s2 , L = 0.25 m/s4 , and t is the time in seconds. At t = 6.0 s, the fuel is exhausted and the rocket is under the influence of gravity alone. Assume air resistance and the rocket’s change in mass are negligible.
(a) Calculate the magnitude of the net impulse exerted on the rocket from t = 0 to t = 6.0 s.
(b) Calculate the speed of the rocket at t = 6.0 s.
(c)
i. Calculate the kinetic energy of the rocket at t = 6.0 s.
ii. Calculate the change in gravitational potential energy of the rocket-Earth system from t = 0 to t = 6.0 s.
(d) Calculate the maximum height reached by the rocket relative to its launching point.
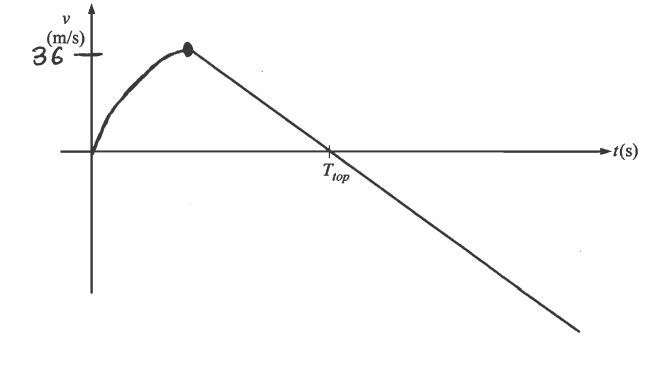
(e) On the axes below, assuming the upward direction to be positive, sketch a graph of the velocity v of the rocket as a function of time t from the time the rocket is launched to the time it returns to the ground. Ttop represents the time the rocket reaches its maximum height. Explicitly label the maxima with numerical values or algebraic expressions, as appropriate.
Answer/Explanation
Ans:
(a)
\(\Delta j = \int Fdt\) \(\int_{0}^{6}4.5 – 0.125t^{2}dt\)
a = 9 – 0.25 t2
F = ma = 4.5 – 0.125 t2 18 N.s
(b)
a = 9-0.25 t2
\(\frac{dv}{dt}= 9-0.25 t^{2}\)
\(\int 1dv = \int (9-0.25t^{2})dt\)
\(V_{6}= 9t – \frac{0.25}{3}t^{3}+C^{v-0}\)
t = 6
V(6) = 36 m/s
(c)
i.
\(\frac{1}{2}(0.5)(36^{2})=KE\)
KE = 324 J
ii.
\(\int V(t)=\int 9t – \frac{0.25}{3}+t^{3}\)
\(x(t)=4.5t^{2} – \frac{0.25}{12}+t^{4}+C^{v-0}\)
t = 6
x = 135 meter Δ PE
ΔPE = mgΔh = (0.5)(9.8)(135) = 661.5 J
(d)
Vi = 36 m/s
Vf = 0 m/s \({V_{f}}^{2}= {V_{i}}^{2}+2a\Delta X\)
a = -9.8 m/s2 0 = 1296 + 2( – 9.8) ΔX
ΔX = 66.12 meters ΔX = 66.12
135 + 66.12
201.12 meters
(e)