Question
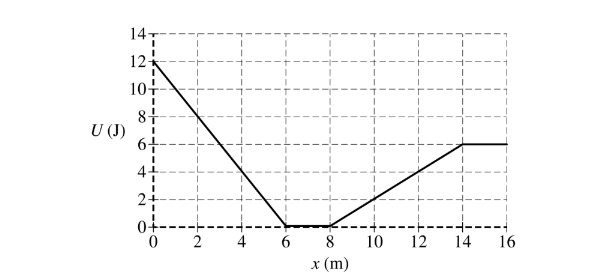
The variable x represents the position of particle A in a two-particle system. Particle B remains at rest. The above graph shows the potential energy U ( x) of the system as a function of position x of particle A, which has a mass of 0.40 kg. Particle A is released from rest at the position x = 2.0 m. Assume positive to be toward the right.
(a) Calculate the speed of particle A when it reaches position x = 14.0 m.
(b) i. Calculate the magnitude of the acceleration of particle A when it reaches position x= 3.0 m.
ii. What is the direction of the acceleration of particle A when it reaches position x= 3.0 m? Left Right
(c) Determine the magnitude of the acceleration of particle A when it reaches position x = 7.0 m.
(d) Particle A is again released from rest at the position x = 2.0 m.
i. Calculate the elapsed time for particle A to travel from position x = 2.0 m to position x = 6.0 m.
ii. Calculate the elapsed time for particle A to travel from position x = 6.0 m to position x = 8.0 m.
iii. Calculate the elapsed time for particle A to travel from position x = 8.0 m to position x = 14 m.
(e) Particle A is now placed at position x= 7.0 m. In order for particle A to reach the position x = 16.0 m and to be moving at a speed of 1.0 m s, what initial speed should particle A be given at its new initial position of x = 7.0 m?
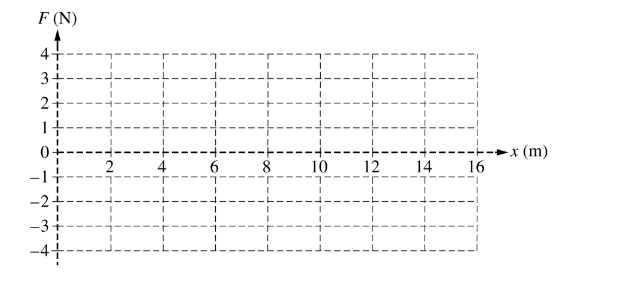
(f) On the grid below, carefully draw a graph of the force F acting on particle A as a function of x for the range 0 < x < 16 m.
Answer/Explanation
(a) For correctly using conservation of energy \(U_1+K_1=U_2+K_2\) \(U_1+0=U_2+\frac{1}{2}mv^2\) For correctly substituting values from the graph into the equation above
\((8j)=(6j)+\left ( \frac{1}{2} \right )(0.40kg)v^2\)
\(v=3.16m/s\)
(b)
i) For correctly relating the slope of the line to the force exerted on the particle \(F=-slope=-\frac{(U_2-U_1)}{(X_2-X_1)}=-\frac{(12-0)J}{(0-6)M}=2.0N\)
For using Newton’s second law to calculate the acceleration of the particle \(a=\frac{F}{m}=\frac{(2.0N)}{(0.40kg)}=5.0/s^2\)
Note: point is awarded for \(5.0 m/ s^2\)
(b)
i) Alternate Solution
Solving for two velocities between 2.0 m and 6.0 m\( v_1 = 0\)

ii) For selecting answer consistent with part (b)(i)
(c) For a correct answer \(F=-slope=0\therefore a=0\) Note: credit is given even if no work is shown
(d)
i) For using a correct kinematic equation to calculate the time
\(d=v_1t+\frac{1}{2}at^2=0+\frac{1}{2}at^2\)
For correctly substituting acceleration from part (b)(i) into equation above
\(t=\sqrt{\frac{2d}{a}}=\frac{(2)(6.0-2.0)m}{(5.0m/s^2)}=1.26s\)
ii) For using a correct kinematic equation to determine the speed at x = 6.0 m or using the velocity at 6.0 m from alternate solutions part (b)(i) or (d)(i)
\(v^2_2=v^2_1+2ad=0+2ad
v_2=\sqrt{2ad}=\sqrt{(2)(5.0m/s^2)(6.0-2.0)m} v_{2}=6.32m/s
For using a kinematic equation for zero acceleration to calculate the time d =vt
\(t=\frac{d}{v}=\frac{(8.0-6.0)m}{(6.32m/s)}\) t=0.32s
Alternate Solution
For correctly using the energy equation to solve for the speed at 6.0 m (or using the value from alternate solution part (b)(i)
\(U_{1}+K_{1}=U_{2}+K_{2} \therefore (8J) +0+\frac{1}{2}(0.40kg)v^{2}_{2} v_{2}=6.32m/s\)
For using a kinematic equation with zero acceleration to calculate the time d=vt\( t=d/v=(8.0-6.0)m/(6.32m/s) t=0.32s\)
(d)
iii) For using a correct kinematic equation to calculate the time
\(d=\frac{1}{2}(v_1+v_2)t\)
\(t=\frac{2d}{(v_1+v_2)}=\frac{(2)(14-8.0)m}{(6.32m/s+3.16m/s)} t=1.26s\)
(e) For correctly using conservation of energy to calculate the speed
\(U_1+K_1=U_2+K_2\)
\(0+\frac{1}{2}m_1v^2_1\)
\(0+\frac{1}{2}m_1v^2_1=U_2+\frac{1}{2}m_2v^2_2\)
\(\left ( \frac{1}{2} \right )(0.40kg)v^2_1=(6j)+\left ( \frac{1}{2} \right )(0.40kg)(1.0m/s^2)
v=5.57m/s\)
(f) For a horizontal line at F = 2 N from x = 0 m to x = 6 m
For a horizontal line at F = 0 from x = 6 m to x = 8 m and from x = 14 m to x = 16 m
For a horizontal line at F = –1 N from x = 8 m to x = 14 m
Note: Two points earned if shape and magnitudes are correct but graph is inverted
Question
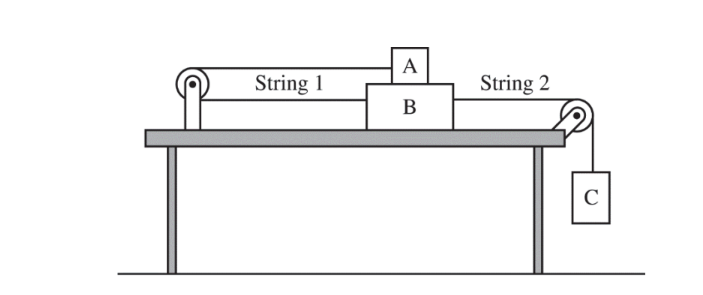
Three blocks are connected by strings that pass over pulleys of negligible mass. Block B is on a level,mhorizontal surface of negligible friction. Block A is on top of block B. String 1 connects blocks A and B. The coefficients of static and kinetic friction between blocks A and B are \(\mu _s\) and \(\mu _k\), respectively. Block C is hanging over the end of the table and is attached to block B by string 2, as shown above. The masses of blocks A, B, and C are\( m_A\) , \(m_B\), and \(m_C\) , respectively. When block C is released, the system remains at rest.
(a)
i. On the dot below, which represents block A, draw and label the forces (not components) that act on block A. Each force must be represented by a distinct arrow starting on, and pointing away from, the dot.
Block A

ii. On the dot below, which represents block B, draw and label the forces (not components) that act on block B. Each force must be represented by a distinct arrow starting on, and pointing away from, the dot.
Block B

(b) Derive an expression for the maximum value for \(m_C\) at which the blocks will remain at rest. Express all algebraic answers in terms of \(\mu _s\), \(\mu _k\) , \(m_A \), \(m_B\),\( m_C\) , and physical constants, as appropriate.
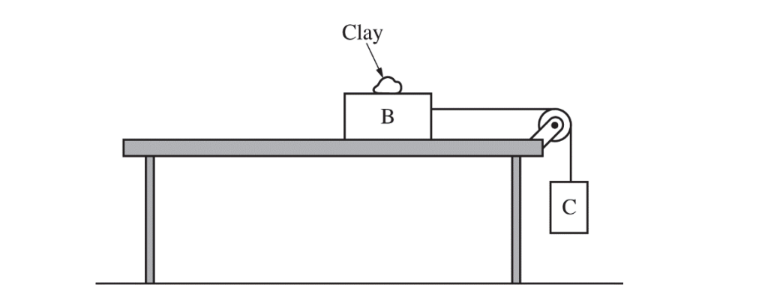
The setup is modified, as shown in the figure above. Block A and one of the pulleys are removed, and block B remains on the table. There is still negligible friction between block B and the table. A lump of clay is added to block B. The students use Newton’s second law to derive an equation for the acceleration \(a_C\) of block C. The acceleration is given by the equation \(a_c=m_cg/m_{tot}\), where \(m_{tot} \)is the combined mass of the clay and the two blocks. Students use the setup shown above to experimentally determine the acceleration g due to gravity. In each trial, a student moves a small amount of clay from block B to block C and then releases the blocks from rest, recording the new values of \(m_C\) and \(a_C\). The total mass of the clay and the two blocks is \(m_{tot} \)5.0 kg tot . The graph below shows \(a_C\) as a function of \(m_C\), where \(m_C\) is now the combined mass of block C and the mass of clay added to block C.
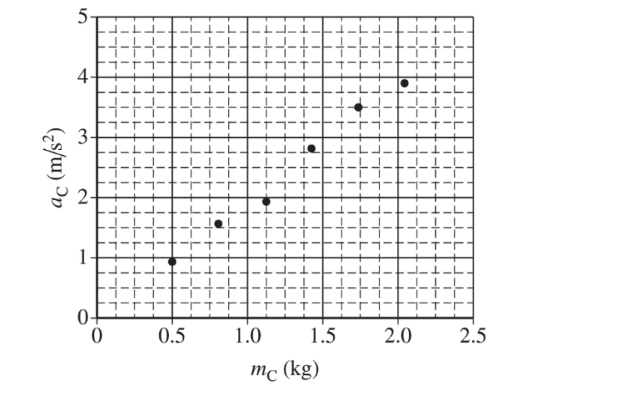
(c)
i. Draw a best-fit line to the data points in the graph above.
ii. Use the best-fit line from part (c)(i) to calculate an experimental value for the acceleration g due to gravity.
(d) If the mass of the pulley in part (c) is significant, would the experimental value of g be greater than, less than, or equal to the value calculated in part (c)
(ii) ? ____ Greater than ____ Less than ____ Equal to Justify your answer.
A different group of students repeats the experiment, but instead of moving clay from block B to block C, they just remove a small amount of clay from block B and set it aside, away from the setup. The equation \(a_c=m_cg/m_{tot}\) still applies to the new experiment.
(e) In order to provide a straight-line graph that can be used to determine an experimental value for g, what two quantities should the students now graph? Check all that apply.

Justify your answer.
Answer/Explanation
(a)(i)
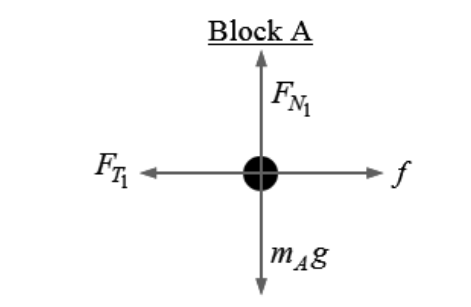
- For correctly drawing and labeling the vertical forces on block A
- For correctly drawing and labeling the horizontal forces on block A
Note: A maximum of one point can be earned if there are any extraneous vectors
(a) (ii)
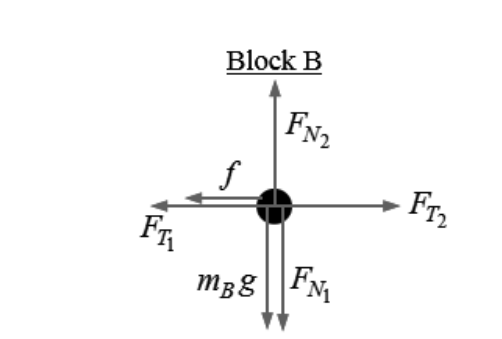
- For correctly drawing and labeling the vertical forces on block B
- For correctly drawing and labeling the tension in string 1 to the left and the tension in string 2 to the right on block B
- For correctly drawing and labeling the static friction to the left on block B
Note: A maximum of two points can be earned if there are any extraneous vectors
(b) For an expression of Newton’s second law on block B
![]()
Expression of Newton’s second law on blocks A and C
![]()
![]()
For a correct expression for the frictional force
![]()
![]()
For an answer consistent with part (a)(ii) \(M_C=2\mu _{s}m_A\)
(c)

(i) For drawing an appropriate best-fit line
(c) (ii) For calculating the slope from the best-fit line and not from the data points unless the data points fall on the best-fit line
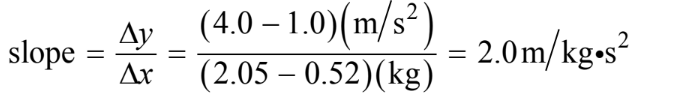
For correctly relating the slope to g
![]()
For calculating an experimental value for g with units
![]()
(d) Select “Less than”
For a correct justification
Example Justification: If the pulley has mass, the system will have more inertia and therefore the acceleration of the system be less. If the acceleration of the system is less, the experimental value of g is less. Note: “Greater than” is accepted if the student provides a reasonable justification.
(e) For selecting “\(a_{c}vs\frac{1}{m_{tot}}\) ” and “\(a_{c}vs\frac{m_c}{m_{tot}}\)”
For a correct justification
Example Justification: By removing the clay, the total mass is a variable. As the total mass of the system is decreased, the acceleration increase; thus\( a_c vs\frac{1}{m_{tot}} \)and \(a_{c}vs\frac{m_c}{m_{tot}}\)will generate a straight line graph that can be used to determine an experimental value for g.