Question
A car is traveling down the highway at speed v when the driver slams on the brakes and skids to a stop in a distance d. Assuming the same frictional force, how far would the car slide if its speed was 2v ?
(A) d /4
(B) d /2
(C) d
(D) 2/d
(E) 4/d
Answer/Explanation
Question
Car A can travel around a curved section of road without skidding at a maximum constant speed of 10 m s. When car B travels around the same curve without skidding at its maximum speed, it has twice the centripetal acceleration as car A. The maximum speed at which car B can safely travel around the curve is most nearly
(A) 5.0 m /s
(B) 10 m /s
(C) 14 m/ s
(D) 20 m /s
(E) 28 m/ s
Answer/Explanation
Questions(a)-(c)
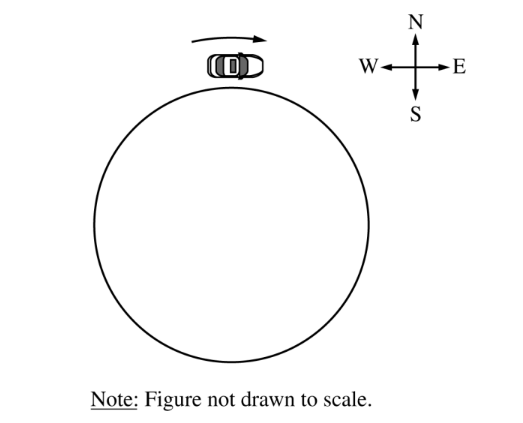
A car is traveling clockwise around a circular racetrack of radius 1440 m. When the car is at the northernmost point on the circle, as shown above, it has a speed of 36.0 m s and is slowing down at a rate of \(1.20 m /s ^2\).
The direction of the velocity of the car is
(A) due east
(B) south of east
(C) due south
(D) south of west
(E) due west
Answer/Explanation
Ans:A.
The direction of velocity is tangent to the circle and in the
Question(b)
The direction of the acceleration of the car is
(A) due east
(B) south of east
(C) due south
(D) south of west
(E) due west
Answer/Explanation
Ans:D
Question(c)
What is the magnitude of the acceleration of the car?
(A) \(0.30 m/ s^2\)
(B)\( 0.90 m/ s^2\)
(C) \( 1.2 m /s^2\)
(D) \( 1.5 m/ s^2\)
(E) \(2.1 m/ s^2\)
Answer/Explanation
Ans:D
The magnitude of acceleration is determined by adding the linear and centripetal accelerations as vectors. The linear acceleration is \(a_L=–1.20m/s^2\). The centripetal acceleration is given by
substituting into the equation \(a_C=\frac{v^2}{r}=\frac{(36.0m/s)^2}{(1440m)}=0.90m/s^2\).
