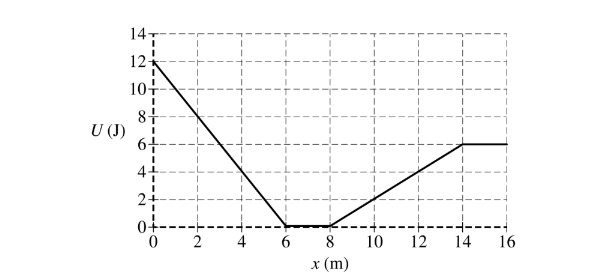
Question
The variable x represents the position of particle A in a two-particle system. Particle B remains at rest. The above graph shows the potential energy U ( x) of the system as a function of position x of particle A, which has a mass of 0.40 kg. Particle A is released from rest at the position x = 2.0 m. Assume positive to be toward the right.
(a) Calculate the speed of particle A when it reaches position x = 14.0 m.
(b) i. Calculate the magnitude of the acceleration of particle A when it reaches position x= 3.0 m.
ii. What is the direction of the acceleration of particle A when it reaches position x= 3.0 m? Left Right
(c) Determine the magnitude of the acceleration of particle A when it reaches position x = 7.0 m.
(d) Particle A is again released from rest at the position x = 2.0 m.
i. Calculate the elapsed time for particle A to travel from position x = 2.0 m to position x = 6.0 m.
ii. Calculate the elapsed time for particle A to travel from position x = 6.0 m to position x = 8.0 m.
iii. Calculate the elapsed time for particle A to travel from position x = 8.0 m to position x = 14 m.
(e) Particle A is now placed at position x= 7.0 m. In order for particle A to reach the position x = 16.0 m and to be moving at a speed of 1.0 m s, what initial speed should particle A be given at its new initial position of x = 7.0 m?
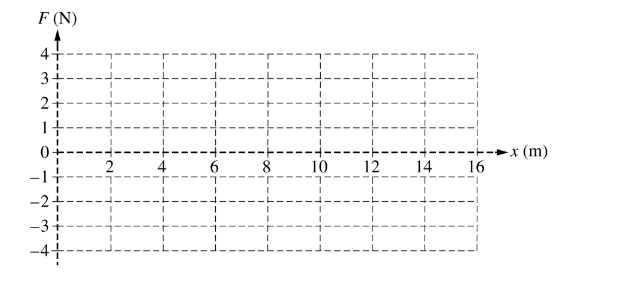
(f) On the grid below, carefully draw a graph of the force F acting on particle A as a function of x for the range 0 < x < 16 m.
Answer/Explanation
(a) For correctly using conservation of energy \(U_1+K_1=U_2+K_2\) \(U_1+0=U_2+\frac{1}{2}mv^2\) For correctly substituting values from the graph into the equation above
\((8j)=(6j)+\left ( \frac{1}{2} \right )(0.40kg)v^2\)
\(v=3.16m/s\)
(b)
i) For correctly relating the slope of the line to the force exerted on the particle \(F=-slope=-\frac{(U_2-U_1)}{(X_2-X_1)}=-\frac{(12-0)J}{(0-6)M}=2.0N\)
For using Newton’s second law to calculate the acceleration of the particle \(a=\frac{F}{m}=\frac{(2.0N)}{(0.40kg)}=5.0/s^2\)
Note: point is awarded for \(5.0 m/ s^2\)
(b)
i) Alternate Solution
Solving for two velocities between 2.0 m and 6.0 m\( v_1 = 0\)

ii) For selecting answer consistent with part (b)(i)
(c) For a correct answer \(F=-slope=0\therefore a=0\) Note: credit is given even if no work is shown
(d)
i) For using a correct kinematic equation to calculate the time
\(d=v_1t+\frac{1}{2}at^2=0+\frac{1}{2}at^2\)
For correctly substituting acceleration from part (b)(i) into equation above
\(t=\sqrt{\frac{2d}{a}}=\frac{(2)(6.0-2.0)m}{(5.0m/s^2)}=1.26s\)
ii) For using a correct kinematic equation to determine the speed at x = 6.0 m or using the velocity at 6.0 m from alternate solutions part (b)(i) or (d)(i)
\(v^2_2=v^2_1+2ad=0+2ad
v_2=\sqrt{2ad}=\sqrt{(2)(5.0m/s^2)(6.0-2.0)m} v_{2}=6.32m/s
For using a kinematic equation for zero acceleration to calculate the time d =vt
\(t=\frac{d}{v}=\frac{(8.0-6.0)m}{(6.32m/s)}\) t=0.32s
Alternate Solution
For correctly using the energy equation to solve for the speed at 6.0 m (or using the value from alternate solution part (b)(i)
\(U_{1}+K_{1}=U_{2}+K_{2} \therefore (8J) +0+\frac{1}{2}(0.40kg)v^{2}_{2} v_{2}=6.32m/s\)
For using a kinematic equation with zero acceleration to calculate the time d=vt\( t=d/v=(8.0-6.0)m/(6.32m/s) t=0.32s\)
(d)
iii) For using a correct kinematic equation to calculate the time
\(d=\frac{1}{2}(v_1+v_2)t\)
\(t=\frac{2d}{(v_1+v_2)}=\frac{(2)(14-8.0)m}{(6.32m/s+3.16m/s)} t=1.26s\)
(e) For correctly using conservation of energy to calculate the speed
\(U_1+K_1=U_2+K_2\)
\(0+\frac{1}{2}m_1v^2_1\)
\(0+\frac{1}{2}m_1v^2_1=U_2+\frac{1}{2}m_2v^2_2\)
\(\left ( \frac{1}{2} \right )(0.40kg)v^2_1=(6j)+\left ( \frac{1}{2} \right )(0.40kg)(1.0m/s^2)
v=5.57m/s\)
(f) For a horizontal line at F = 2 N from x = 0 m to x = 6 m
For a horizontal line at F = 0 from x = 6 m to x = 8 m and from x = 14 m to x = 16 m
For a horizontal line at F = –1 N from x = 8 m to x = 14 m
Note: Two points earned if shape and magnitudes are correct but graph is inverted
Question
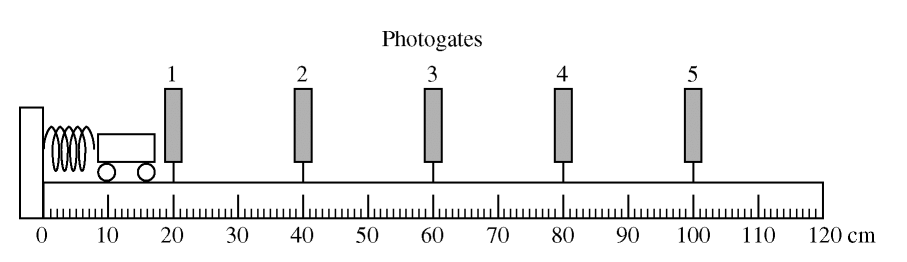
In an experiment, a student wishes to use a spring to accelerate a cart along a horizontal, level track. The spring is attached to the left end of the track, as shown in the figure above, and produces a nonlinear restoring force of magnitude Fs = As2 + Bs, where s is the distance the spring is compressed, in meters. A measuring tape, marked in centimeters, is attached to the side of the track. The student places five photogates on the track at the locations shown.
(a) Derive an expression for the potential energy U as a function of the compression s. Express your answer in terms of A, B, s, and fundamental constants, as appropriate.
In a preliminary experiment, the student pushes the cart of mass 0.30 kg into the spring, compressing the spring 0.040 m. For this spring, A = 200 N/m2 and B = 150 N/m. The cart is released from rest. Assume friction and air resistance are negligible only during the short time interval when the spring is accelerating the cart.
(b) Calculate the following:
i. The speed of the cart immediately after it loses contact with the spring
ii. The impulse given to the cart by the spring
In a second experiment, the student collects data using the photogates. Each photogate measures the speed of the cart as it passes through the gate. The student calculates a spring compression that should give the cart a speed of 0.320 m s after the cart loses contact with the spring. The student runs the experiment by pushing the cart into the spring, compressing the spring the calculated distance, and releasing the cart. The speeds are measured with a precision of ±0.002 m s. The positions are measured with a precision of ±0.005 m.
| Photogate | 1 | 2 | 3 | 4 | 5 |
| Cart speed (m/s) | 0.412 | 0.407 | 0.399 | 0.374 | 0.338 |
| Photogate position (m) | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 |
(c) On the axes below, plot the data points for the speed v of the cart as a function of position x. Clearly scale and label all axes, as appropriate.

(d)
i. Compare the speed of the cart measured by photogate 1 to the predicted value of the speed of the cart just after it loses contact with the spring. List a physical source of error that could account for the difference.
ii. From the measured speed values of the cart as it rolls down the track, give a physical explanation for any trend you observe.
Answer/Explanation
Ans:
(a)
v = – Ws
\(v = – \int_{0}^{s}\left ( AS^{2}+BS \right )ds\)
\(v = – \left [ \frac{AS^{3}}{3}+\frac{BS^{2}}{2} \right ]\)
(b) i.
\(\frac{(200)(.040)^{3}}{3}+\frac{(150)(.040)^{2}}{2}=\frac{1}{2}(-3)v^{2}\)
\(v = .91, \frac{M}{S}\)
ii.
J = MΔV
= .30 (.91)
J = .273
(c)
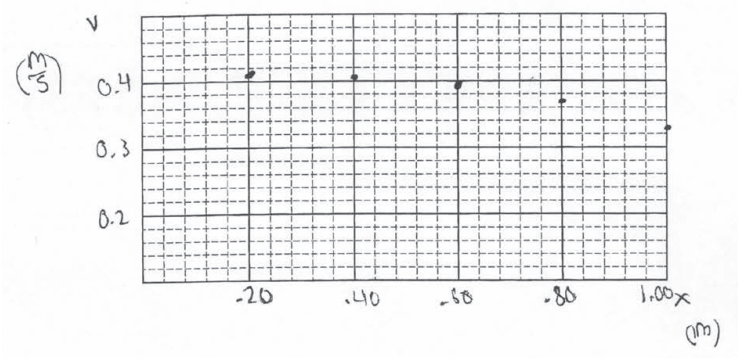
(d) i.
\(.320\frac{M}{S} \) \(.412\frac{M}{S} \)
The student pushes the court back too far causing the resulting impulse from the spring to be greater.
ii.
a frictional force causes an acceleration that opposes the carts vel. causing it to slow down.
Question
A narrow tunnel is drilled through Earth (mass = M, radius = R), connecting points P and Q, as shown in the diagram on the left below. The perpendicular distance from Earth’s center, C, to the tunnel is x. A package (mass = m) is dropped from Point P into the tunnel; its distance from P is denoted y and its distance from C is denoted r. See the diagram on the right.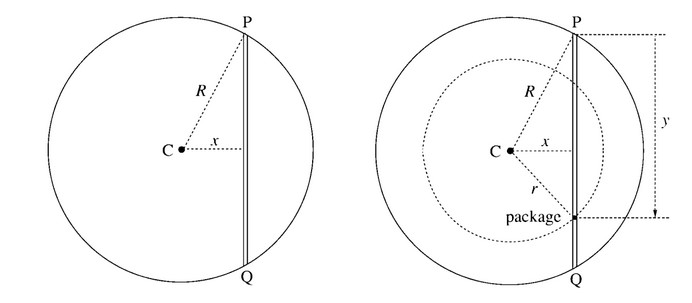
(a) Assuming that Earth is a homogeneous sphere, the gravitational force Fon the package is due to m and the mass contained within the sphere of radius r < R. Use this fact to show that \(F=-\frac{GMm}{R^3} r\)
(b) Use the equation F(r) = -dU/dr to find an expression for the change in gravitational potential energy of the package as it moves from Point P to a point where its distance from Earth’s center is r. Write your answer in terms of G, M, m, R, and r.
(c) Apply Conservation of Energy to determine the speed of the package in terms of G, M, R, x, and y. (Ignore friction.)
(d) (i) At what point in the tunnel-that is, for what value of y-will the speed of the package be maximized?
(ii) What is this maximum speed? (Write your answer in terms of G, M, R, and x.)
Answer/Explanation
Ans:
(a) The mass contained in a sphere of radius r< R is
\(M_{within r}= pV_{within r} = \frac{M}{\frac{4}{3} \pi R^3}(\frac{4}{3} \pi r^3) = \frac{r^3}{R^3} M\)
so
\(F= -\frac{Gm}{r^2}(\frac{r^3}{R^3} M)= -\frac{GMm}{R^3}r\)
(b) Since dU = – F(r) dr,
\(\Delta U |_R^r = \int_{R}^{r} dU = \int_{R}^{r} -F(r) dr=\int_{R}^{r}\frac{GMm}{R^3}r dr = \frac{GMm}{R^3}[\frac{1}{2}r^2]_R^r =\frac{GMm}{2R^3}(r^2 – R^2)\)
(c) Conservation of Energy, \(K_i + U_i = K_f + U_f\), can be written in the form \(\Delta K = -\DeltaU\), which gives
\(\frac{1}{2} mv^2 = -\frac{GMm}{2R^3}(r^2-R^2)\)
\(v=\sqrt{\frac{GM}{R^3}(R^2-r^2)}\)
By applying the Pythagorean theorem to the two right triangles in the figure,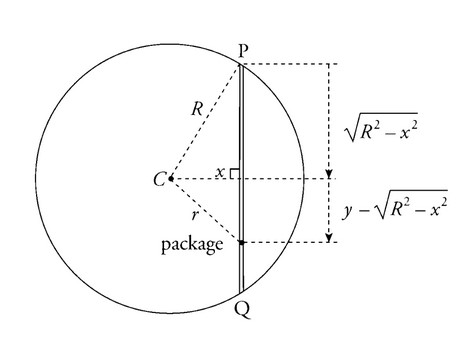
we see that
\(r^2 = x^2 + (y- \sqrt{R^2-x^2})^2\)
so the expression given above for v can be rewritten in the form
\( v = \sqrt{\frac{GM}{R^3}[R^2 -x^2 – (y – \sqrt{R^2 -x^2)^2]}\)
\(=\sqrt{\frac{GM}{R^3}[2y \sqrt{R^2 -x^2}-y^2]}\).
(d) (i) From the expression derived in part (c) above, we can see that the value of y which will maximum v is
\(y = \sqrt{R^2-x^2}\)
This is the midpoint of the tunnel.
(ii) The maximum value for v is
\(v_{max}=\sqrt{\frac{GM}{R^3}[R^2-x^2]}\)