Question
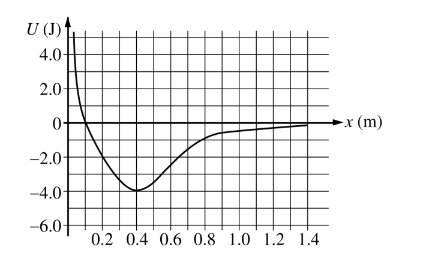
The variable x represents the position of particle A in a two-particle system. Particle B remains at rest. The graph above shows potential energy U of the system as a function of x .
If the total energy of the system is -2.0 J, which of the following statements is true?
(A) The system has zero potential energy.
(B) Particle A has 2.0 J of kinetic energy.
(C) The system has 2.0 J of total mechanical energy.
(D) Particle A is always at x = 0.40 m.
(E) Particle A oscillates between x = 0.20 m and 0.65 m.
Answer/Explanation
An object of mass 0.5 kg is given an initial velocity and then slides across a horizontal surface. The object experiences a resistive force that is a function of velocity. The velocity v of the object as a function of time t is given by \(v(t)=\alpha e^{-\beta t}\)=,where\( \alpha =2m/s\) and\( \beta =3s^{-1}\).
Question
Which of the following is a correct expression for the net force, in newtons, exerted on the object as a function of time?
(A)\(6e^{-3t}\)
(B)\(-3e^{-3t}\)
(C)\(e^{-3t}\)
(D)\(2e^{-3t}\)
(E)\(\frac{2}{3\left ( 1-e^{-3t} \right )}\)
Answer/Explanation
Ans:B
The acceleration is the derivative of the velocity, \(a=\frac{dv}{dt}=\frac{dv}{t}(\alpha e^{\beta t})=-\beta \alpha e^{-\beta t}\)Substituting into an equation for
Newton’s second law yields
\(F_{net}=ma=m-\beta \alpha e^{-\beta t}\)
Question

The variable x represents the position of particle A in a two-particle system. Particle B remains at rest. The graph above shows potential energy U of the system as a function of x .
The x-component of the force on particle A when it is at x = 0.15 m is most nearly
(A) –20 N
(B) –2.0 N
(C) –1.0 N
(D) 2.0 N
(E) 20 N
Answer/Explanation
Question
A particle is subjected to a conservative force whose potential energy function is
\(U(x) = (x-2)^3 – 12x\)
where U is given in joules when x is measured in meters. Which of the following represents a position of stable equilibrium?
(A)x= -4
(B) x = -2
(C) X = 0
(D) x = 2
(E) X = 4
Answer/Explanation
Ans: E
Points of equilibrium occur when dU/ dx is equal to zero:
\(\frac{dU}{dx} = 0 \Rightarrow 3(x – 2)^2 – 12 = 0 \Rightarrow (x-2)^2 = 4 \Rightarrow x = 0\) or \(x = 4\)
There’s more than one way to determine which equilibrium
points are stable equilibrium points. One way is to graph
U(x) and see which equilibrium point is a minimum. Another
way is to use the first derivative. The following explanation
uses the second derivative test, but feel free to use the
method you’re most comfortable with. Points of stable
equilibrium occur when dU/dx = o and \(d^2 U/dx^2\) is positive (because then the equilibrium point is a relative minimum).
Since
\(\frac{dU}{dx} = 6 (x – 2)\)
the point x = 4 is a point of stable equilibrium (x = o is
Question
A particle’s kinetic energy is changing at a rate of -6.o J / s when its speed is 3.0 m/ s. What is the magnitude of the force on the particle at this moment?
(A) 0.5 N
(B) 2.0 N
(C) 4.5 N
(D) 9.0 N
(E) 18 N
Answer/Explanation
Ans: B
Differentiate the equation \(K = \frac{1}{2} mv^2\) with respect to time:
\(\frac{dK}{dt} = \frac{1}{2} m. 2v \frac{dv}{dt} = mv \frac{dv}{dt} = v. m \frac{dv}{dt} = v . ma =vF\)
This tells us that
\(F= \frac{dK/dt}{v} = \frac{-6.0 J/s}{3.0 m/s}= -2 N\)
