Question
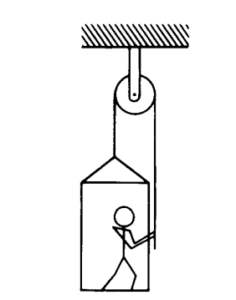
The figure above shows an 80-kilogram person standing on a 20-kilogram platform suspended by a rope passing over a stationary pulley that is free to rotate. The other end of the rope is held by the person. The masses of the rope and pulley are negligible. You may use g = 10 m/ s2. Assume that friction is negligible, and the parts of the rope shown remain vertical.
a. If the platform and the person are at rest, what is the tension in the rope?
The person now pulls on the rope so that the acceleration of the person and the platform is 2 m/s2 upward.
b. What is the tension in the rope under these new conditions?
c. Under these conditions, what is the force exerted by the platform on the person?
After a short time, the person and the platform reach and sustain an upward velocity of 0.4 m/ s.
d. Determine the power output of the person required to sustain this velocity.
Answer/Explanation
Ans:
a. Combining the person and the platform into one object, held up by two sides of the rope we have ΣF = ma;
2T = (80 kg + 20 kg)g giving T = 500 N
b. Similarly, ΣF = ma; 2T – 1000 N = (100 kg)(2 m/s2) giving T = 600 N
c. For the person only: ΣF = ma; N + 600 N – mg = ma gives N = 360 N
d. P = Fv = mgv = 400 W
Question
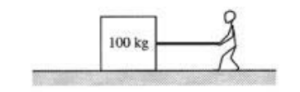
The 100 kg box shown above is being pulled along the x-axis by a student. The box slides across a rough surface, and its position x varies with time t according to the equation x = 0.5t3 + 2t, where x is in meters and t is in seconds.
a. Determine the speed of the box at time t = 0.
b. Determine the following as functions of time t.
i. The kinetic energy of the box
ii. The net force acting on the box
iii. The power being delivered to the box
c. Calculate the net work done on the box in the interval t = 0 to t = 2s.
d. Indicate below whether the work done on the box by the student in the interval t = 0 to t = 2s would be greater than, less than, or equal to the answer in part (c).
_____Greater than _____Less than _____Equal to
Justify your answer
Answer/Explanation
Ans:
a. v = dx/dt = 1.5t2 + 2
v0 = 2 m/s
b. i. K = ½ mv2 = 50(1.5t2 + 2)2
ii. Fnet = ma = m(dv/dt) = m(3 t) = 300 t
iii. P = Fv = (300 t)(1.5t2 + 2) = 450t3 + 600t OR P =dK/dt
c. W = ∆K; v(2) = 8 m/s, v(0) = 2 m/s; W = ½ m(8 m/s)2– ½ m(2 m/s)2 = 3000 J
Alternately, 𝑊 = ∫ 𝑃𝑑𝑡
d. Greater, the student had to perform work against friction
