Question
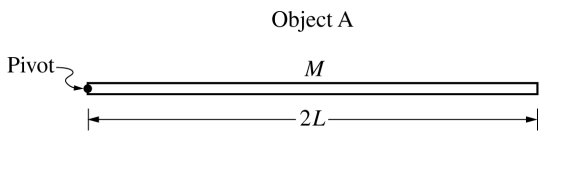
Object A is a long, thin, uniform rod of mass M and length 2L that is free to rotate about a pivot of negligible friction at its left end, as shown above.
(a) Using integral calculus, derive an expression to show that the rotational inertia IA of object A about the pivot is given by \(\frac{4}{3}ML^{2}\) .
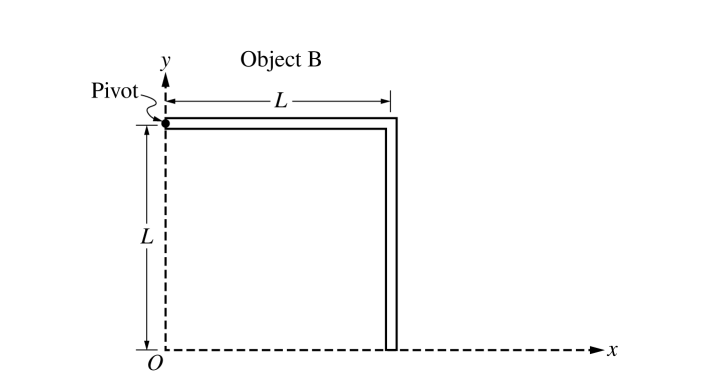
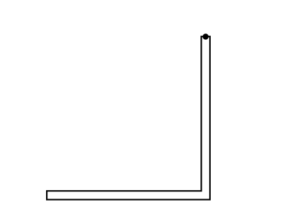
Object B of total mass M is formed by attaching two thin, uniform, identical rods of length L at a right angle to each other. Object B is held in place, as shown above. Express your answers in part (b) in terms of L .
(b) Determine the following for the given coordinate system shown in the figure.
i. The x-coordinate of the center of mass of object B
ii. The y-coordinate of the center of mass of object B
Object B has a rotational inertia of IB about its pivot.
(c) Is the value of IB greater than, less than, or equal to IA ?
_____ Greater than _____ Less than _____ Equal to
Justify your answer.
Object B is released from rest and begins to rotate about its pivot.
(d) On the axes below, sketch graphs of the magnitude of the angular acceleration α and the angular speed ω of object B as functions of time t from the time it is released to the time its center of mass reaches its lowest point.
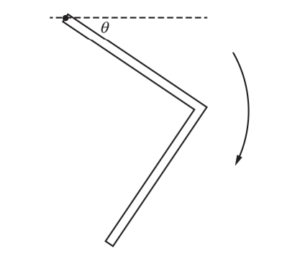
(e) While object B rotates from the horizontal position down through the angle θ shown above, is the magnitude of its angular acceleration increasing, decreasing, or not changing?
_____ Increasing _____ Decreasing _____ Not changing
Justify your answer.
Object B rotates through the position shown above.
(f) Derive an expression for the angular speed of object B when it is in the position shown above. Express your answer in terms of M , L , IB , and physical constants, as appropriate.
Answer/Explanation
Ans:
(a)
I = MR2 \(dm = \frac{m}{2L}dx\)
dI = dmr2 \(I = \int_{0}^{2L}\frac{m}{2L}r^{2}dr\)
\(I = \frac{m}{2L}\int_{0}^{2L}r^{2}dr\)
\(I = \frac{m}{2L}_{4}^{0}\textrm{}\left ( \frac{1}{5}r ^{3}|_{0}^{2L}\right )\)
\(I = \frac{m8L^{2}}{6L}=\frac{4}{3}ML^{2}\)
(b)
i. Each bunch mass m/2
\(X_{am}=\frac{\sum x_{i}m_{i}}{m_{total}}=\frac{\left ( \frac{L}{2} \right )\left ( \frac{M}{2} \right )+L\left ( \frac{M}{2} \right )}{m}=\frac{\frac{3ml}{4}}{m}=\frac{3}{4}L\)
ii.
\(Y_{am}=\frac{\sum x_{i}m_{i}}{m_{total}}=\frac{\left ( \frac{L}{2} \right )\left ( \frac{M}{2} \right )+L\left ( \frac{M}{2} \right )}{m}=\frac{\frac{3ml}{4}}{m}=\frac{3}{4}L\)
(c)
√ Less than
Object as must is distributed further anny thus the phot up to distance 2l1 while object B mast is distributed closer to the point.
(d)
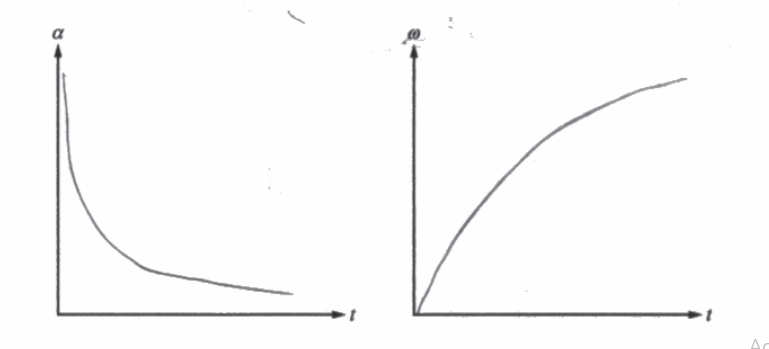
(e)
√ Decreasing
As it rotates towards eunhilibrium, the ampronent of gravity tangent to the motion of its center of mass devengds, so its aneleatun also devenges.
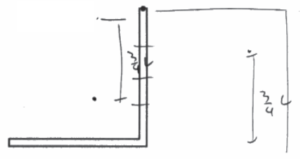
(f)
PE los!
\(mgh =\left ( \frac{1}{2}L \right )(10Lm = 5ML)\)
averted to statements kBs \(w = \sqrt{\frac{10ML}{I_{B}}}\)
1/2 Iw2 = 5ML
Iw2 = 10 ML
Question
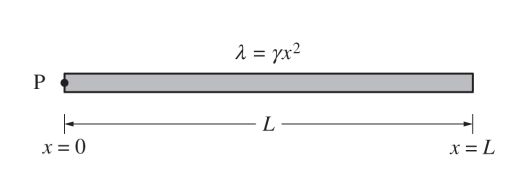
A triangular rod of length L and mass M has a nonuniform linear mass density given by the equation λ = γx2, where \(\gamma =\frac{3M}{L^{3}}\) and x is the distance from point P at the left end of the rod.
(a) Using integral calculus, show that the rotational inertia I of the rod about an axis perpendicular to the page and through point P is \(\frac{3}{5}ML^{2}.\)
(b) Determine the horizontal location of the center of mass of the rod relative to point P. Express your answer in terms of L.
(c) For an axis perpendicular to the page, is the value of the rotational inertia of the rod around point P greater than, less than, or equal to the value of the rotational inertia of the rod around the rod’s center of mass?
_____ Greater than _____ Less than _____ Equal to
Justify your answer.
The rod is released from rest in the position shown, and the rod begins to rotate about a horizontal axis perpendicular to the page and through point P.
(d) On the axes below, sketch graphs of the magnitude of the net torque τ on the rod and the angular speed ω of the rod as functions of time t from the time the rod is released until the time its center of mass reaches its lowest point.
(e) As the rod rotates from the horizontal position down through vertical, is the magnitude of the angular acceleration on the rod increasing, decreasing, or not changing?
_____ Increasing _____ Decreasing _____ Not changing
Justify your answer.
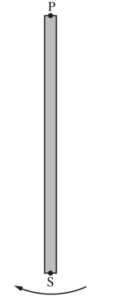
(f) The mass of the rod is 3.0 kg, and the length of the rod is 1.0 m. Calculate the linear speed v of point S as the rod swings through the vertical position shown.
Answer/Explanation
Ans:
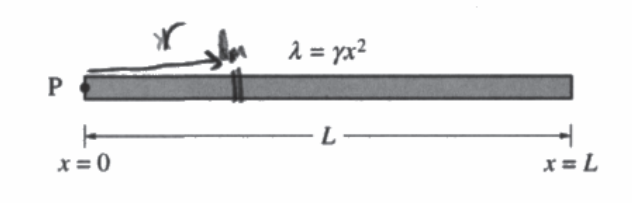
(a)
dm = λdx
= δr2dr
\(I = \int r^{2}dm\rightarrow I = \int_{0}^{L}\delta x^{4}dx=\frac{\delta x^{5}}{5}|_{0}^{L}=\frac{\delta L^{5}}{5}-0\)
\(\Rightarrow I = \frac{3M}{L^{3}}\left ( \frac{\delta L^{5}}{5} \right )\rightarrow I = \frac{3ML^{2}}{5}\)
\(I = \frac{3ML^{2}}{5}\)
(b)
\(X_{cm}=\frac{\int rdm}{M}\Rightarrow X_{cm}=\frac{\int_{0}^{L}\delta r3dr}{M}\rightarrow X_{cm}=\frac{\delta r^{4}}{4M}|_{0}^{L}\Rightarrow X_{cm}==\frac{\delta L^{4}}{4M}-0\)
\(X_{cm}=\frac{3M}{L^{3}}\left ( \frac{L^{4}}{4M} \right )\rightarrow X_{cm}=\frac{3}{4}L\)
(c)
√ Greater than
This is became if the rod were ratating e its counter of mass, then the mass would be more centered around the axis then if it were rotating e point P.
(d)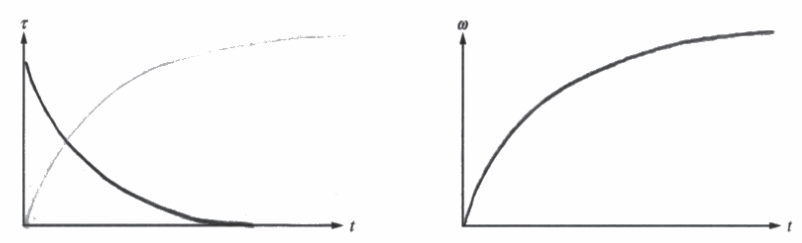
(e)
√ Decreasing
As the rod rotating, it follows ∑τ = Ix
\(\sum \tau =\tau_{g} =\overrightarrow{r}. \times \overrightarrow{F_{g}},\) which has a decreasing magnitude as when the bar rotates, the component of gravity perpendicular to the radius decreases. Thus, the magnitude of angular acceleration decreases.
(f)
\(E_{g} = E_{x}\rightarrow mgh = \frac{1}{2}I\omega^{2} \)
\(mg\frac{3}{4}L = \frac{1}{2}\left ( \frac{3mL^{2}}{5} \right )\omega ^{2}\rightarrow \frac{3mg}{4}L=\frac{3mL^{2}}{10}\)
Question
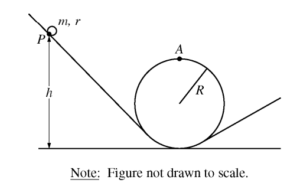
The rotational inertia of a rolling object may be written in terms of its mass m and radius r as I = bmr2, where b is a numerical value based on the distribution of mass within the rolling object. Students wish to conduct an experiment to determine the value of b for a partially hollowed sphere. The students use a looped track of radius R >> r, as shown in the figure above. The sphere is released from rest a height h above the floor and rolls around the loop.
(a) Derive an expression for the minimum speed of the sphere’s center of mass that will allow the sphere to just pass point A without losing contact with the track. Express your answer in terms of b, m, R, and fundamental constants, as appropriate.
(b) Suppose the sphere is released from rest at some point P and rolls without slipping. Derive an equation for the minimum release height h that will allow the sphere to pass point A without losing contact with the track.
Express your answer in terms of b, m, R, and fundamental constants, as appropriate.
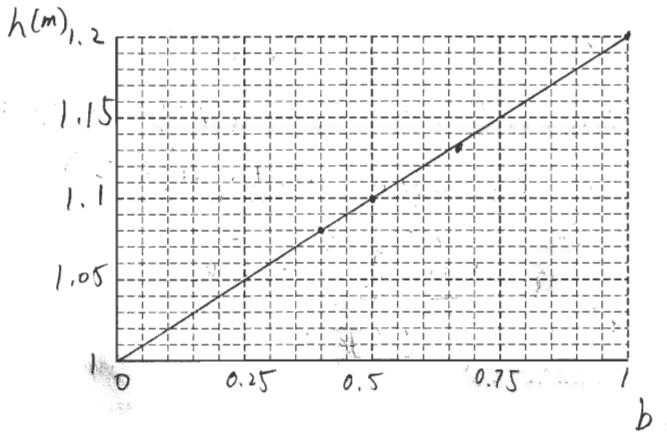
The students perform an experiment by determining the minimum release height h for various other objects of radius r and known values of b. They collect the following data.
| Object | b | h(m) |
| Solid sphere | 0.40 | 1.08 |
| Hollow sphere | 0.67 | 1.13 |
| Solid cylinder | 0.50 | 1.10 |
| Hollow cylinder | 1.0 | 1.20 |
(c) On the grid below, plot the release height h as a function of b. Clearly scale and label all axes, including units, if appropriate. Draw a straight line that best represents the data.
(d) The students repeat the experiment with the partially hollowed sphere and determine the minimum release height to be 1.16 m. Using the straight line from part (c), determine the value of b for the partially hollowed sphere.
(e) Calculate R, the radius of the loop.
(f) In part (b), the radius r of the rolling sphere was assumed to be much smaller than the radius R of the loop. If the radius r of the rolling sphere was not negligible, would the value of the minimum release height h be greater, less, or the same?
________Greater ________Less ________The same
Justify your answer.
Answer/Explanation
Ans:
(a)
\(\frac{mv^{2}}{R}= mg\)
\(v^{2}= Rg\) \(v= \sqrt{Rg}\)
(b)
\(mgh = \frac{1}{2}mRg + 2mgR + \frac{1}{2}\cdot bmr^{2}\left ( \frac{\sqrt{Rg}}{r} \right )^{2}\)
\(gh = \frac{1}{2}Rg + 2Rg + \frac{1}{2}\cdot b\cdot Rg\)
\(h = \frac{1}{2}R + 2R + \frac{1}{2}bR\)
(c)
(d)
Used points (0.5, 1.1) and (1, 1.2) for slope
slope = \(\frac{1.2+1.1}{1-0.5}=\frac{0.1}{0.5}=\frac{1}{5}\) y – intercept at (0, 1)
\(1.16 = \frac{1}{5}\cdot b + 1\) b = 0.8
(e)
\(h = \frac{1}{2}R + 2R + \frac{1}{2}bR\) using point (1, 1.2)
\(1.2 = 2\frac{1}{2}R + \frac{1}{2}R\)
1.2 = 3R
R = 0.4 m
(f)
X Less
The sphere will have a lower center of mass at the top of the loop, thus requiring a smaller centripetal acceleration. So the velocity at the top also does not need to be as high, meaning that the initial potential energy, which is determined partly by the release height, can be less.
