Question

A student sets up an experiment with a cart on a level horizontal track. The cart is attached with an elastic cord to a force sensor that is fixed in place on the left end of the track. A motion sensor is at the right end of the track, as shown in the figure above. The cart is given an initial speed of v0 = 2.0 m s and moves with this constant speed until the elastic cord exerts a force on the cart. The motion of the cart is measured with the motion detector, and the force the elastic cord exerts on the cart is measured with the force sensor. Both sensors are set up so that the positive direction is to the left. The data recorded by both sensors are shown in the graphs of velocity as a function of time and force as a function of time below.

(a) Calculate the mass m of the cart. For time period from 0.50 s to 0.75 s, the force F the elastic cord exerts on the cart is given as a function of time t by the equation F A = sin(ωt) , where A = 6.3 N and ω = 12.6 rad/s.
(b) Using the given equation, show that the area under the graph above is 1.0 N .s
(c) The experiment is repeated using a different cord that exerts a larger average force on the cart. The cart starts and ends with the same speeds as those in the original experiment. Will the area for the graph of force as a function of time for the new cord be greater than, less than, or equal to the area for that of the original cord? ____ Greater than ____ Less than ____ Equal to Justify your answer. The elastic cord from the original experiment can be modeled as an ideal spring with force constant k .
(d) Derive an expression for the maximum change in length \(x_{MAX}\) for the cord. Express your answer in terms of m, k, \(v_0\) , and physical constants, as appropriate.
The student performs several trials of the experiment. For the first trial, the cart is empty. In each succeeding trial, a block is added to the cart. In all trials, the cart has an initial speed of 2.0 m s to the right, the cart rebounds to the left with a speed of 2.0 m s , and the maximum change in length of the elastic cord is measured. The total mass M of the cart and the maximum change in length of the cord in each trial are recorded in the table below.
(e) Indicate below which quantities should be graphed to yield a straight line with a slope that could be used to calculate a numerical value for the force constant of the elastic cord k. Vertical axis:
Horizontal axis: Use the remaining columns in the table on the previous page, as needed, to record any quantities that you indicated that are not given.
(f) Plot the data points for the quantities indicated in part (e) on the graph below. Clearly scale and label all axes, including units as appropriate. Draw a straight line that best represents the data.
(g) Use the best-fit line to calculate the force constant k of the elastic cord.
Answer/Explanation
(a) For correctly using the area under the graph to calculate the mass of the cart j=Area = \(\Delta p=m(v_2-V_1)\) For a correct answer with units \(m=\frac{Area}{(v_2-v_1)}\)=\(\frac{(1.0N.s)}{(2.0m/s-(-2.0m/s))}\) m = 0.25 kg
(b) For relating the time integral of given equation to the area under the curve For applying the correct limits of integration
\(j=Area=\int_{0.50}^{0.75}Asin(\omega t)dt\)
\(j=-\frac{A}{\omega }[cos\omega t]_{0.50}^{0.75}=-\frac{(6.3N)}{(12.6rad/s)}[cos(12.6t)]_{0.50}^{0.75}\)
\(j=-(0.50)(cos[12.6(0.75)])-cos[(12.6)(0.50)]\)
\(j=1.0N.s\)
(c) For selecting “Equal to” with an attempt at a relevant justification For a correct justification Example: Since the cart starts and ends at the same velocity, the impulse on the cart will be the same so the area under the graph will be the same. Note: If the wrong selection is made, the justification is ignored.
(d) For correctly using conservation of energy
\(U_{MAX}=K_{MAX}\)
\(\frac{1}{2}kx^{2}_{MAX}=\frac{1}{2}mv_{0}v^2\)
\(x_{MAX}=v_{0}\sqrt{\frac{m}{k}}\)
(e) For correctly indicating two variables that will yield a straight line that could be used to determine a value for Example: Vertical Axis: \(x_{MAX}\) Horizontal Axis:\(\sqrt{m}\)
Note: Student earns full credit if axes are reversed or if they use another acceptable combination
(f) For a correct scale that uses more than half the grid 1 point For correctly labeling the axis with variables and units consistent with part (e) Note: Student earns full credit if axes are reversed
For correctly plotting data For drawing a straight line consistent with the plotted data
(g) For correctly calculating the slope from the best-fit line and not the data points
Example: \(slope=\frac{\Delta x_{MAX}}{\Delta \sqrt{m}}=\frac{(0.40-0.20)m}{(1.32-0.70)\sqrt{kg}}=0.34m/\sqrt{kg} 0.33m/\sqrt{kg}\)
\(\frac{v_{0}}{\sqrt{k}}\therefore k=\frac{v^2_{0}}{(slope)^2}=\frac{(2.0m/s)^2}{(0.34m/\sqrt{kg})^2}\) k=34.6N/m
(linear reression k=36.7N/m)
Question
A toy rocket of mass 0.50 kg starts from rest on the ground and is launched upward, experiencing a vertical net force. The rocket’s upward acceleration a for the first 6 seconds is given by the equation a = K- Lt2 , where K = 9.0 m/s2 , L = 0.25 m/s4 , and t is the time in seconds. At t = 6.0 s, the fuel is exhausted and the rocket is under the influence of gravity alone. Assume air resistance and the rocket’s change in mass are negligible.
(a) Calculate the magnitude of the net impulse exerted on the rocket from t = 0 to t = 6.0 s.
(b) Calculate the speed of the rocket at t = 6.0 s.
(c)
i. Calculate the kinetic energy of the rocket at t = 6.0 s.
ii. Calculate the change in gravitational potential energy of the rocket-Earth system from t = 0 to t = 6.0 s.
(d) Calculate the maximum height reached by the rocket relative to its launching point.
(e) On the axes below, assuming the upward direction to be positive, sketch a graph of the velocity v of the rocket as a function of time t from the time the rocket is launched to the time it returns to the ground. Ttop represents the time the rocket reaches its maximum height. Explicitly label the maxima with numerical values or algebraic expressions, as appropriate.
Answer/Explanation
Ans:
(a)
\(\Delta j = \int Fdt\) \(\int_{0}^{6}4.5 – 0.125t^{2}dt\)
a = 9 – 0.25 t2
F = ma = 4.5 – 0.125 t2 18 N.s
(b)
a = 9-0.25 t2
\(\frac{dv}{dt}= 9-0.25 t^{2}\)
\(\int 1dv = \int (9-0.25t^{2})dt\)
\(V_{6}= 9t – \frac{0.25}{3}t^{3}+C^{v-0}\)
t = 6
V(6) = 36 m/s
(c)
i.
\(\frac{1}{2}(0.5)(36^{2})=KE\)
KE = 324 J
ii.
\(\int V(t)=\int 9t – \frac{0.25}{3}+t^{3}\)
\(x(t)=4.5t^{2} – \frac{0.25}{12}+t^{4}+C^{v-0}\)
t = 6
x = 135 meter Δ PE
ΔPE = mgΔh = (0.5)(9.8)(135) = 661.5 J
(d)
Vi = 36 m/s
Vf = 0 m/s \({V_{f}}^{2}= {V_{i}}^{2}+2a\Delta X\)
a = -9.8 m/s2 0 = 1296 + 2( – 9.8) ΔX
ΔX = 66.12 meters ΔX = 66.12
135 + 66.12
201.12 meters
(e)
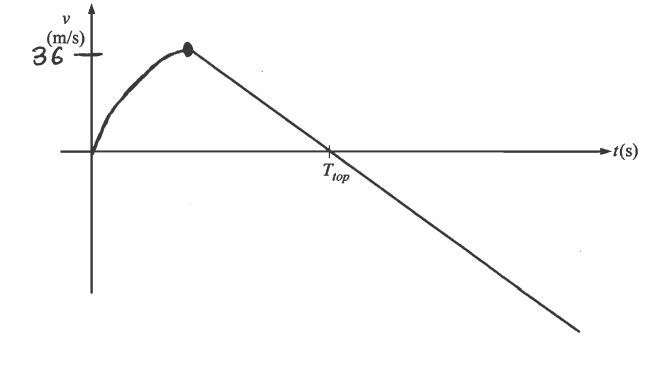
Question
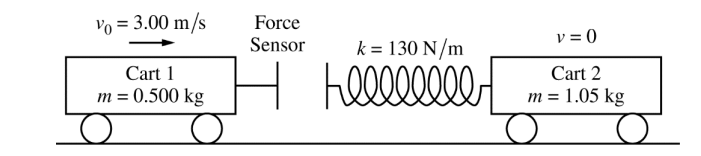
Two carts are on a horizontal, level track of negligible friction. Cart 1 has a sensor that measures the force exerted on it during a collision with cart 2, which has a spring attached. Cart 1 is moving with a speed of v0 = 3.00 m/s 0 toward cart 2, which is at rest, as shown in the figure above. The total mass of cart 1 and the force sensor is 0.500 kg, the mass of cart 2 is 1.05 kg, and the spring has negligible mass. The spring has a spring constant of k = 130 N/m.The data for the force the spring exerts on cart 1 are shown in the graph below. A student models the data as the quadratic fit F = (3200 N/s2 )t2 – (500 N/s )t .
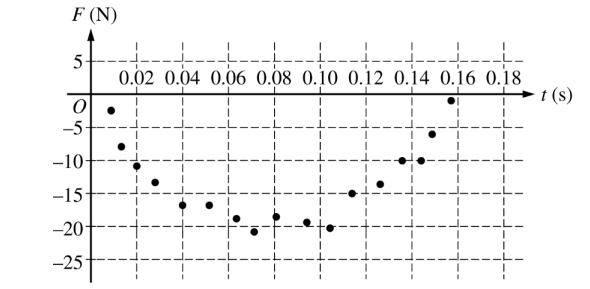
(a) Using integral calculus, calculate the total impulse delivered to cart 1 during the collision.
(b)
i. Calculate the speed of cart 1 after the collision.
ii. In which direction does cart 1 move after the collision?
____ Left ____ Right
____ The direction is undefined, because the speed of cart 1 is zero after the collision.
(c)
i. Calculate the speed of cart 2 after the collision.
ii. Show that the collision between the two carts is elastic.
(d)
i. Calculate the speed of the center of mass of the two-cart–spring system.
ii. Calculate the maximum elastic potential energy stored in the spring.
Answer/Explanation
Ans:
(a)
\(F = \frac{dp}{dt}\) \(\frac{3200 + 3}{3} – \frac{500+2}{2}\int_{t=0}^{t = 0.16}\)
dp = Fdt
\(\Delta P = \int_{t_{0}}^{tf}Fdt\) \(\frac{3200(.16)^{3}}{3}-\frac{500(.16)^{1}}{2}\)
\(=\int_{0}^{0.16}\left ( 3200t^{2}-500t \right )dt\) = -2.03 kg. m. s-1
(b) i.
ΔP = mΔv = -2.03
\(\Delta V = \frac{-2.03}{0.500}=-4.06 m/s\)
Vf = V0 + ΔV = 3.00 – 4.06 = -1.06 → 1.06 m/s
ii.
X Left
(c) i.
By Newton’s 3rd law of conservation of momentum:
ΔP1 = -ΔP2
ΔP2 = +2.03 = m2ΔV2
ΔV2 = \(\frac{+2.03}{1.05}=1.933 m/s\)
Vf2 = V02 + ΔV2 = 0 + 1.933 = 1.933 m/s
ii.
KE0 : KEf (elastic condition)
KE0 : \(\frac{1}{2}(0.500)(3)^{2}=2.25\)
KEf : \(\frac{1}{2}(0.500)(1.06)^{2}+\frac{1}{2}(1.05)(1.933)^{2}=2.24\)
2.25 ≈ 2.24, thus elision is elastic
(d) i.
∑P = ∑m (Vcom)
\(V_{com}=\frac{\sum P}{\sum m}=\frac{m_{2}v_{1}}{m_{1}+m_{2}}=\frac{0.500(3)}{0.500+1.05}=0.968 m/s\)
ii.
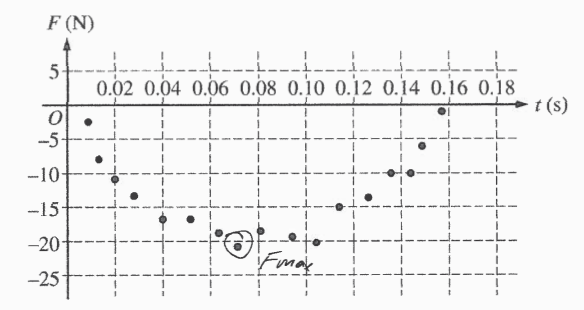
\(U_{max}=\frac{1}{2}Kx_{max}\)
\(F_{max}=Kx_{max}, \) \(x_{max} = \frac{F_{max}}{K}\approx \frac{21}{130}=.161\)
\(U_{max} = \frac{1}{2}(130)(0.161)=10.465 J\)
