Question
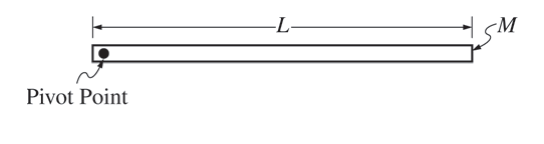
A uniform, thin rod of length L and mass M is allowed to pivot about its end, as shown in the figure above.
(a) Using integral calculus, derive the rotational inertia for the rod around its end to show that it is ML2/3 .
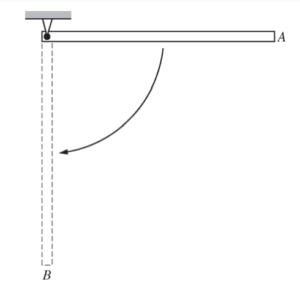
The rod is fixed at one end and allowed to fall from the horizontal position A through the vertical position B.
(b) Derive an expression for the velocity of the free end of the rod at position B. Express your answer in terms of M, L, and physical constants, as appropriate.
An experiment is designed to test the validity of the expression found in part (b). A student uses rods of various lengths that all have a uniform mass distribution. The student releases each of the rods from the horizontal position A and uses photogates to measure the velocity of the free end at position B. The data are recorded below.
| Length (m) | 0.25 | 0.50 | 0.75 | 1.00 | 1.25 | 1.50 |
| Velocity (m/s) | 2.7 | 3.8 | 4.6 | 5.2 | 5.8 | 6.3 |
(c) Indicate below which quantities should be graphed to yield a straight line whose slope could be used to calculate a numerical value for the acceleration due to gravity g.
Horizontal axis: _________________________
Vertical axis: _________________________
Use the remaining rows in the table above, as needed, to record any quantities that you indicated that are not given. Label each row you use and include units.
(d) Plot the straight line data points on the grid below. Clearly scale and label all axes, including units as appropriate. Draw a straight line that best represents the data.

(e)
i. Using your straight line, determine an experimental value for g.
ii. Describe two ways in which the effects of air resistance could be reduced.
Answer/Explanation
Ans:
(a)
 dI – dmR2
dI – dmR2
\(I = \int_{0}^{L}dI = \int_{0}^{L}dmR^{2}=\int_{0}^{L}\lambda x^{2}dx =\lambda \left [ \frac{x^{3}}{3} \right ]_{0}^{L}=\frac{ML^{2}}{3}\)
(b)
\(Co M = \frac{L}{2}\)
\(\Delta PE = Mg\frac{L}{2}=\frac{1}{2}IW^{2}\) \(MgL = \frac{ML^{2}}{3}\) \(\frac{3g}{L}= \frac{V^{2}}{L^{2}}\)
\(W = \frac{V}{L}\) \(V = \sqrt{3gL}\)
| Length (m) | 0.25 | 0.50 | 0.75 | 1.00 | 1.25 | 1.50 |
| Velocity (m/s) | 2.7 | 3.8 | 4.6 | 5.2 | 5.8 | 6.3 |
| Square Velocity (m2/s2) | 7.3 | 14 | 21 | 27 | 34 | 40 |
(c)
Horizontal axis: Length
Vertical axis: Square Velocity
(d)
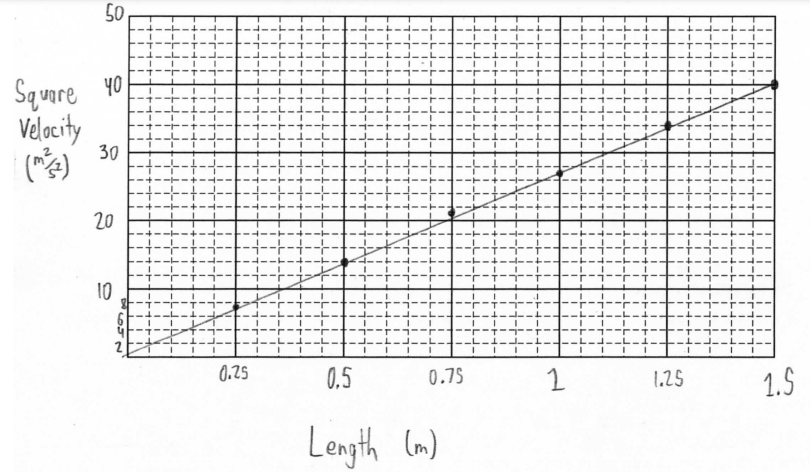
(e) i.
( 0.75, 20)
(1.5, 40) \(3g = \left ( \frac{20}{0.75} \right )=26.7\)
V2 = 3gL g = 8.9
ii.
Air resistance could be reduced by using a heavier rod or a thinner rod.
Question
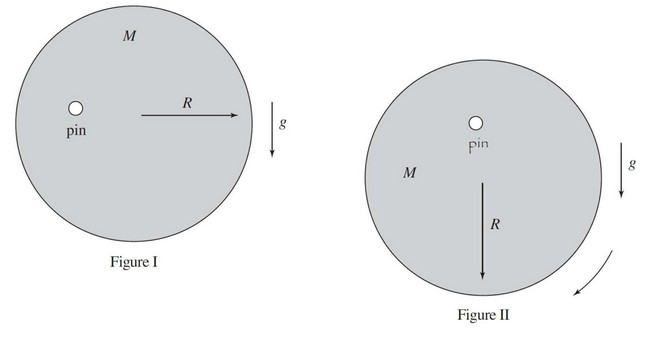
A disk of mass M and radius R is pinned half of the way along its radius, and held in a horizontal position, as shown in Figure I. The rotational inertia of the disk about its center is \(\frac{1}{2} MR^2\). The disk is released at t = o s, and falls to the vertical position shown in Figure II, and it continues to rotate about the pin. Answer the following in terms of M, R, and g.
(a) Calculate the rotational inertia of the disk about the pin.
(b) Calculate the angular acceleration of the disk at t = o s.
(c) Calculate angular velocity of the disk when it is in the vertical position shown in Figure II.
Now the disk is stopped and brought to rest in the vertical position shown in Figure II. It is given a slight disturbance to an angle \(\theta _0\).
(d) Calculate the angular frequency of the oscillation.
Answer/Explanation
Ans:
(a) Use the parallel axis theorem to determine the rotational inertia of the object about the pin.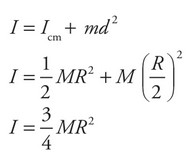
(b) When the object is first released, gravity provides a torque about the pin causing the disk to rotate about the pin. A free-body diagram for the disk is shown below.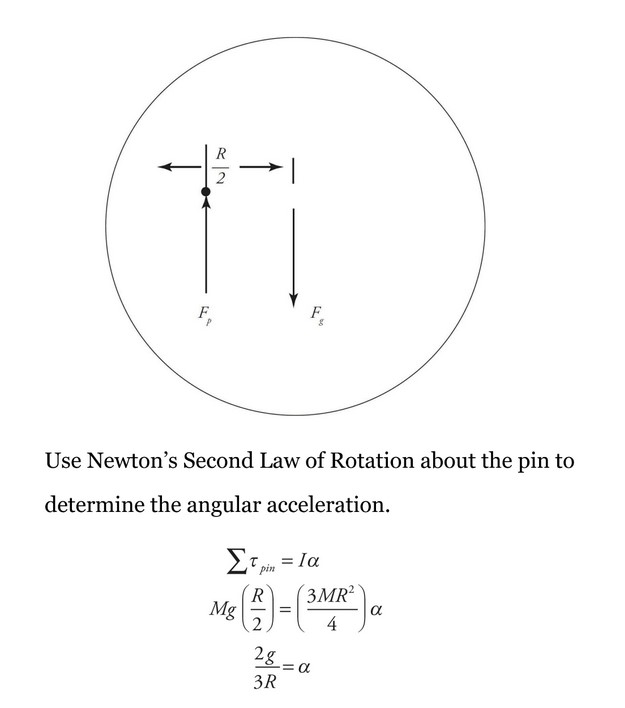
(c) Use the Law of Conservation of Mechanical Energy to determine the angular velocity at the vertical position. All the initial gravitational potential energy is converted into rotational kinetic energy. The center of mass falls half the distance of the radius. 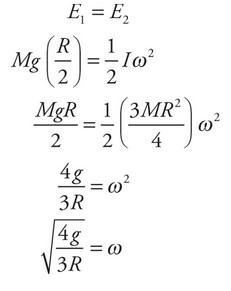
(d) Now the disk is undergoing simple harmonic motion because it is undergoing small angle oscillations. Derive a differential equaiton fo the form \(\frac{d^2x}{dt^2}= – \omega ^2 x\) to determine \(\omega \). Start with Newton’s Second Law of Rotation to end up with a differential equation because \(a = \frac{d^2 \theta}{dt^2}\)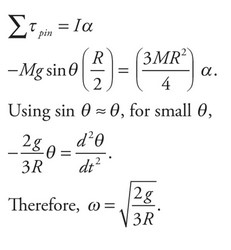
Question
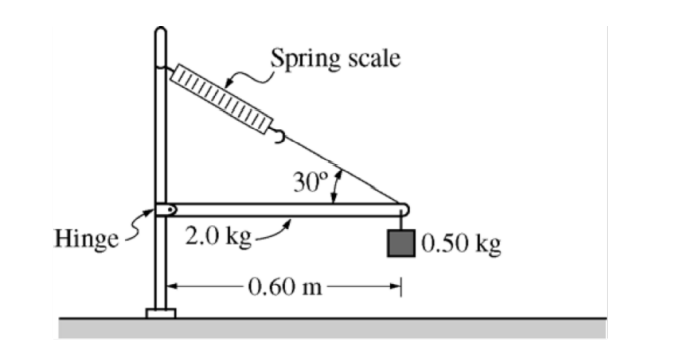
The horizontal uniform rod shown above has length 0.60 m and mass 2.0 kg. The left end of the rod is attached to a vertical support by a frictionless hinge that allows the rod to swing up or down. The right end of the rod is supported by a cord that makes an angle of 30° with the rod. A spring scale of negligible mass measures the tension in the cord. A 0.50 kg block is also attached to the right end of the rod.
a. On the diagram below, draw and label vectors to represent all the forces acting on the rod. Show each force vector originating at its point of application.
![]()
b. Calculate the reading on the spring scale.
The rotational inertia of a rod about its center is \(\frac{1}{12}ML^{2}\) , where M is the mass of the rod and L is its length.
c. Calculate the rotational inertia of the rod-block system about the hinge.
d. If the cord that supports the rod is cut near the end of the rod, calculate the initial angular acceleration of the rod-block system about the hinge.
Answer/Explanation
Ans:
a. 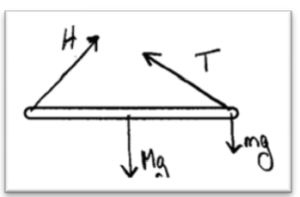
b. Στ = 0
About the hinge: TL sin 30º – mgL – Mg(L/2) = 0 gives T = 29 N
c. Itotal = Irod + Iblock where Irod,end = Icm + MD2 = ML2/12 + M(L/2)2 = ML2/3
Itotal = ML2/3 + mL2 = 0.42 kg-m2
d. Στ = Iα
mgL + MgL/2 = Iα gives α = 21 rad/s2
