Question
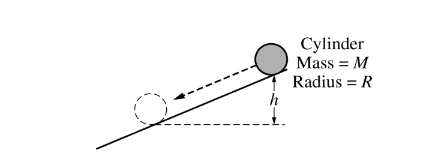
A cylinder of mass M and radius R is released from rest at the top of an inclined plane, as shown above. The cylinder rolls without slipping down the incline. The rotational inertia of the cylinder is \(MR ^2/2\) .
(a) Derive an expression for the angular momentum of the cylinder about its center of mass when it has rolled a vertical distance h. Express your answer in terms of M, R, h, and physical constants, as appropriate.
(b) Is the angular momentum of the cylinder conserved as the cylinder rolls down the vertical distance h ? Yes No Justify your answer.
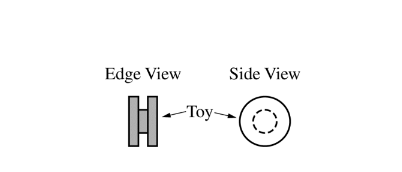
A child’s toy is composed of 3 narrow cylinders attached around a common axis through their centers, as shown above. The central cylinder has a mass M and radius R. Each of the two outer cylinders has a mass M and radius 2R.
(c) Derive an expression for the rotational inertia of the toy around its center. Express your answer in terms of M, R, and physical constants, as appropriate.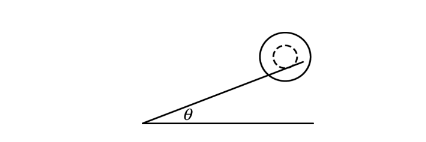
The toy is placed on a narrow track that is inclined at an angle of θ above the horizontal. Only the central cylinder is in contact with the track, as shown above. The toy rolls without slipping down the track.
(d)
i. On the dot below, which represents the toy, draw and label the forces (not components) that act on the toy. The dashed line is parallel to the narrow track. Each force must be represented by a distinct arrow starting on, and pointing away from, the dot.
ii. Derive an expression for the linear acceleration of the toy as it rolls down the track. Express your answer in terms of M, R, θ , and physical constants, as appropriate.
iii. Determine the force of friction exerted on the toy as it rolls down the track. Express your answer in terms of M, R, θ , and physical constants, as appropriate.
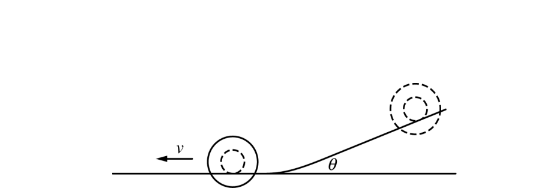
(e) The toy reaches the bottom of the incline and rolls at constant speed v along a horizontal section of the track, as shown above. Derive an expression for the total kinetic energy of the toy while it is rolling. Express your answer in terms of M, R, v, and physical constants, as appropriate.
Answer/Explanation
(a) For correctly using conservation of energy\( U_{g1}+K_1=U_{g2}+K_2 U_{g1}+0=0+K_2\)
\(mgh=\frac{1}{2}mv^2+\frac{1}{2}I\omega ^2\)
For correctly substituting into equation above for both linear and rotational kinetic energy
\(Mgh=\frac{1}{2}M(R\omega )^2+\frac{1}{2}\left ( \frac{MR^2}{2} \right )\omega ^2 gh=\frac{3}{4}R^2\omega ^2 \omega =\sqrt{\frac{4gh}{3R^2}}\)
For correctly substituting into the equation for angular momentum \(L=I\omega =\left ( \frac{MR^2}{2} \right )\left ( \sqrt{\frac{4gh}{3R^2}} =MR\sqrt{\frac{gh}{3}} \right )\)
(b) Selecting “No” For a correct justification Example: The frictional force exerts an external torque on the cylinder therefore the angular momentum of the cylinder is not conserevd. Example: The angular velocity is changing with h; therefore, L is changing.
(c) For setting the total rotational inertia for the toy equal to the sum of the rotaional inertias of the three cylinders \(T_tot=2I_{OUTER}+I_{INNER}=2\frac{MR^2}{2}_{OUTER}+\left ( \frac{MR^2}{2}_{INNER} \right )
I_{tot}=2\left ( \frac{M(2R)^2}{2} \right )+\left ( \frac{MR^2}{2} \right )=4MR^2+\frac{MR^2}{2}
I_{tot}=\frac{9}{2}MR^2\)
(d)i) For correctly drawing a vector representing the normal force perpendicular to the dashed line For correctly drawing a vector representing the weight of the toy directed straight down For correctly drawing a vector representing the frictional force directed up the incline Note: A maximum of two points can be earned if there are any extraneous vectors
ii) For correctly using Newton’s second law in linear form for the toy on the incline
\(F=ma\therefore (3M)g(sin\theta)-F_f=(3M)a
\varsigma =Ia\therefore F_fR=\left ( \frac{9}{2}MR^2 \right )\left ( \frac{a}{R} \right )\therefore F_f=\frac{9}{2}Ma
3Mg(sin\theta)-\frac{9}{2}Ma=3Ma\therefore 3g(sin\theta)=\frac{15}{2}a
a=\frac{2}{5}g(sin\theta)\)
(d) For an answer consistent with part (d)(ii)
iii) \(F_f=\frac{9}{2}M\left ( \frac{2}{5}g(sin\theta) \right )=\frac{9}{5}Mg(sin\theta)\)
(e) For using both rotational and linear kinetic energy for the total kinetic energy of the toy
\(K=K_L+K_R=\frac{1}{2}mv^2+\frac{1}{2}I\omega ^2\)
For correctly substituting for both the rotational inertia, the mass, and \(\omega =v/R\) into the equation above
\(K=\frac{1}{2}(3M)v^2+\frac{1}{2}\left ( \frac{9}{2}MR^2 \right )\omega ^2=\frac{3}{2}Mv^2+\frac{9}{4}MR^2\left ( \frac{v}{R} \right )^2=\frac{15}{4}Mv^2\)
Question

A cylinder of mass M and radius R is released from rest at the top of an inclined plane, as shown above. The cylinder rolls without slipping down the incline. The rotational inertia of the cylinder is \(MR ^2/2\) .
(a) Derive an expression for the angular momentum of the cylinder about its center of mass when it has rolled a vertical distance h. Express your answer in terms of M, R, h, and physical constants, as appropriate.
(b) Is the angular momentum of the cylinder conserved as the cylinder rolls down the vertical distance h ? Yes No Justify your answer.

A child’s toy is composed of 3 narrow cylinders attached around a common axis through their centers, as shown above. The central cylinder has a mass M and radius R. Each of the two outer cylinders has a mass M and radius 2R.
(c) Derive an expression for the rotational inertia of the toy around its center. Express your answer in terms of M, R, and physical constants, as appropriate.
The toy is placed on a narrow track that is inclined at an angle of θ above the horizontal. Only the central cylinder is in contact with the track, as shown above. The toy rolls without slipping down the track.
(d)
i. On the dot below, which represents the toy, draw and label the forces (not components) that act on the toy. The dashed line is parallel to the narrow track. Each force must be represented by a distinct arrow starting on, and pointing away from, the dot.

ii. Derive an expression for the linear acceleration of the toy as it rolls down the track. Express your answer in terms of M, R, θ , and physical constants, as appropriate.
iii. Determine the force of friction exerted on the toy as it rolls down the track. Express your answer in terms of M, R, θ , and physical constants, as appropriate.

(e) The toy reaches the bottom of the incline and rolls at constant speed v along a horizontal section of the track, as shown above. Derive an expression for the total kinetic energy of the toy while it is rolling. Express your answer in terms of M, R, v, and physical constants, as appropriate.
Answer/Explanation
(a) For correctly using conservation of energy\( U_{g1}+K_1=U_{g2}+K_2 U_{g1}+0=0+K_2\)
\(mgh=\frac{1}{2}mv^2+\frac{1}{2}I\omega ^2\)
For correctly substituting into equation above for both linear and rotational kinetic energy
\(Mgh=\frac{1}{2}M(R\omega )^2+\frac{1}{2}\left ( \frac{MR^2}{2} \right )\omega ^2 gh=\frac{3}{4}R^2\omega ^2 \omega =\sqrt{\frac{4gh}{3R^2}}\)
For correctly substituting into the equation for angular momentum \(L=I\omega =\left ( \frac{MR^2}{2} \right )\left ( \sqrt{\frac{4gh}{3R^2}} =MR\sqrt{\frac{gh}{3}} \right )\)
(b) Selecting “No” For a correct justification Example: The frictional force exerts an external torque on the cylinder therefore the angular momentum of the cylinder is not conserevd. Example: The angular velocity is changing with h; therefore, L is changing.
(c) For setting the total rotational inertia for the toy equal to the sum of the rotaional inertias of the three cylinders \(T_tot=2I_{OUTER}+I_{INNER}=2\frac{MR^2}{2}_{OUTER}+\left ( \frac{MR^2}{2}_{INNER} \right )
I_{tot}=2\left ( \frac{M(2R)^2}{2} \right )+\left ( \frac{MR^2}{2} \right )=4MR^2+\frac{MR^2}{2}
I_{tot}=\frac{9}{2}MR^2\)
(d)i) For correctly drawing a vector representing the normal force perpendicular to the dashed line For correctly drawing a vector representing the weight of the toy directed straight down For correctly drawing a vector representing the frictional force directed up the incline Note: A maximum of two points can be earned if there are any extraneous vectors
ii) For correctly using Newton’s second law in linear form for the toy on the incline
\(F=ma\therefore (3M)g(sin\theta)-F_f=(3M)a
\varsigma =Ia\therefore F_fR=\left ( \frac{9}{2}MR^2 \right )\left ( \frac{a}{R} \right )\therefore F_f=\frac{9}{2}Ma
3Mg(sin\theta)-\frac{9}{2}Ma=3Ma\therefore 3g(sin\theta)=\frac{15}{2}a
a=\frac{2}{5}g(sin\theta)\)
(d) For an answer consistent with part (d)(ii)
iii) \(F_f=\frac{9}{2}M\left ( \frac{2}{5}g(sin\theta) \right )=\frac{9}{5}Mg(sin\theta)\)
(e) For using both rotational and linear kinetic energy for the total kinetic energy of the toy
\(K=K_L+K_R=\frac{1}{2}mv^2+\frac{1}{2}I\omega ^2\)
For correctly substituting for both the rotational inertia, the mass, and \(\omega =v/R\) into the equation above
\(K=\frac{1}{2}(3M)v^2+\frac{1}{2}\left ( \frac{9}{2}MR^2 \right )\omega ^2=\frac{3}{2}Mv^2+\frac{9}{4}MR^2\left ( \frac{v}{R} \right )^2=\frac{15}{4}Mv^2\)
Question
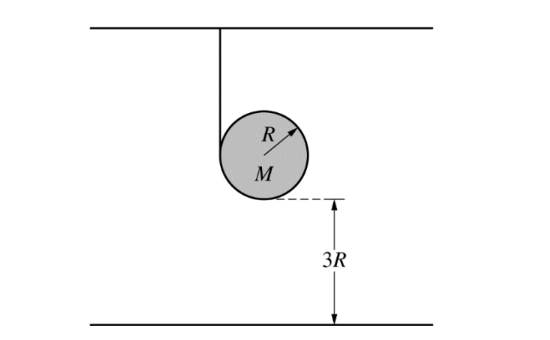
A thin uniform disk of mass M and radius R has a string wrapped around its edge and attached to the ceiling. The bottom of the disk is at a height 3R above the floor, as shown above. The disk is released from rest. The rotational inertia of a disk around its center is \(I = MR ^2/2\) .
(a) On the circle below that represents the disk, draw and label the forces (not components) that act on the disk. Each force must be represented by a distinct arrow starting on, and pointing away from, the disk, beginning at the point where the force is exerted on the disk. The dot is at the center of the disk.
(b) When released from rest, the disk falls and the string unwinds. The force the string exerts on the disk is \(F_T\) , and the gravitational force exerted on the disk is \(F_ g\) . Which of the following expressions correctly relates\( F_T\) and\( F_g \) as the disk falls? ____\( F _T< F_ g \)____ \( F_ T =F_g\) ____ \(F_ T>F_ g \) Justify your answer.
(c) Express all answers in terms of M, R, and physical constants, as appropriate.
i. Derive an expression for the acceleration a of the disk as it falls.
ii. Derive an expression for the time\( \Delta t\) that it takes the disk to reach the ground.
iii. Derive an expression for the rotational kinetic energy \(K_{rot}\) of the disk at the instant it reaches the ground.
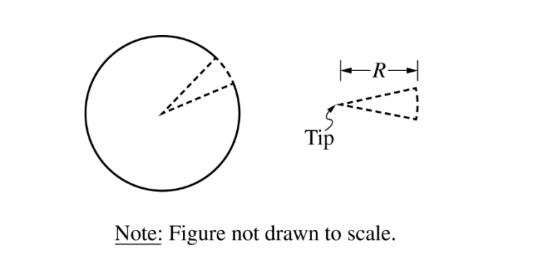
(d) A very narrow wedge is cut out of the thin uniform disk of mass M, as shown above. If r is the distance from the tip of the wedge, then the linear mass density of the wedge can be expressed as follows:
\(\lambda (r)=\frac{Mr}{25R^2}\).
i. Using integral calculus, derive an expression for the rotational inertia of the wedge around its tip.
ii. Derive an expression for the rotational inertia of the modified disk (i.e., the disk after the narrow wedge is cut out) around its original center.
Answer/Explanation
(a)
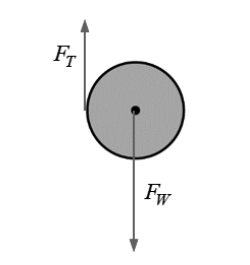
- For drawing and labeling the weight of the block directed downward starting at the center of the disk
- For drawing and labeling the tension directed upward starting at the left edge of the disk
Note: A maximum of one point can be earned if there are any extraneous vectors.
(b) For selecting “\( F_ T <F_ g\)”
For a correct justification
Example Justification: The center of mass of the disk accelerates downward, so the force of gravity must be greater than the tension in the string.
c( i)
- For an expression of Newton’s second law in linear form\( F_{net}=ma \therefore M_g – F_T = Ma\)
- For an expression of Newton’s second law in rotational form\( \varsigma = I_\alpha :. F_TR = \frac{1}{2}MR^2\alpha\)
- For correctly relating the linear and rotational accelerations\( F_{T}R = \frac{1}{2} MR^2(\frac{\alpha }{R})\therefore F_T = \frac{1}{2} Ma \)
- For combining the two equations \(Mg-\frac{1}{2} Ma=Ma \therefore a =\frac{2}{3}g\)
Alternate Solution
- For a clear indication of using the point of contact between the string and the disk as the axis of rotation
- For deriving an expression for the rotational inertia of the disk around an edge \(I = I + Mh^2 = \frac{1}{2} MR^2 + MR^2 = \frac{3}{2}MR^2\)\)
- For an expression of Newton’s second law in rotational form \(\varsigma = I\alpha \therefore MgR = \frac{3}{2} MR^2\alpha \)
- For correctly relating the linear and rotational accelerations\( MgR = \frac{3}{2} MR^2 (\frac{a}{R}) \therefore a=\frac{2}{3}g\)
(c) (ii)
- For correctly substituting the distance into a kinematic equation to calculate the time
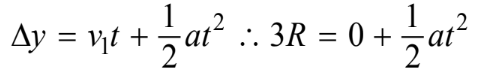
- For substituting the acceleration from part (c)(i) into equation above
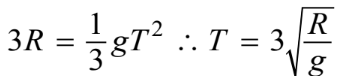
(c)(iii) For correctly substituting into an equation for the the rotational kinetic energy of the disk
![]()
![]()
Alternate solution
For correctly substituting into an equation for the rotational kinetic energy of the disk
![]()
![]()
(d) i. For integrating an appropriate equation to calculate rotational inertia of the wedge
\(I=\int r^2dm\)
\(m=\lambda r\therefore \lambda dr=\frac{Mr}{25R^2}dr\)
For correctly substituting into equation for rotational inertia
![]() For integrating with appropriate limits or constant of integration
For integrating with appropriate limits or constant of integration
![]()
(d)ii. For correctly using superposition to determine the rotational inertia of the disk without the wedge
![]()
