Question
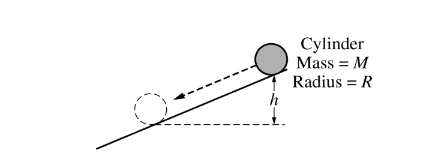
A cylinder of mass M and radius R is released from rest at the top of an inclined plane, as shown above. The cylinder rolls without slipping down the incline. The rotational inertia of the cylinder is \(MR ^2/2\) .
(a) Derive an expression for the angular momentum of the cylinder about its center of mass when it has rolled a vertical distance h. Express your answer in terms of M, R, h, and physical constants, as appropriate.
(b) Is the angular momentum of the cylinder conserved as the cylinder rolls down the vertical distance h ? Yes No Justify your answer.
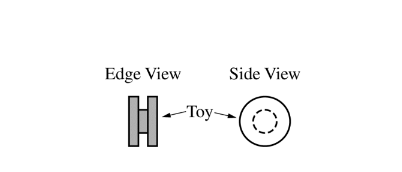
A child’s toy is composed of 3 narrow cylinders attached around a common axis through their centers, as shown above. The central cylinder has a mass M and radius R. Each of the two outer cylinders has a mass M and radius 2R.
(c) Derive an expression for the rotational inertia of the toy around its center. Express your answer in terms of M, R, and physical constants, as appropriate.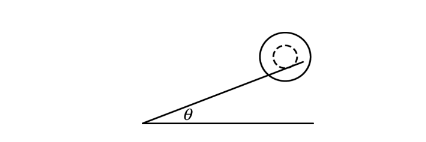
The toy is placed on a narrow track that is inclined at an angle of θ above the horizontal. Only the central cylinder is in contact with the track, as shown above. The toy rolls without slipping down the track.
(d)
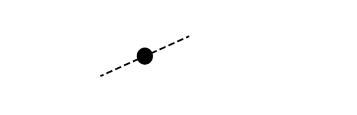
i. On the dot below, which represents the toy, draw and label the forces (not components) that act on the toy. The dashed line is parallel to the narrow track. Each force must be represented by a distinct arrow starting on, and pointing away from, the dot.
ii. Derive an expression for the linear acceleration of the toy as it rolls down the track. Express your answer in terms of M, R, θ , and physical constants, as appropriate.
iii. Determine the force of friction exerted on the toy as it rolls down the track. Express your answer in terms of M, R, θ , and physical constants, as appropriate.
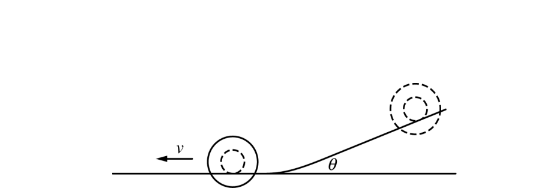
(e) The toy reaches the bottom of the incline and rolls at constant speed v along a horizontal section of the track, as shown above. Derive an expression for the total kinetic energy of the toy while it is rolling. Express your answer in terms of M, R, v, and physical constants, as appropriate.
Answer/Explanation
(a) For correctly using conservation of energy\( U_{g1}+K_1=U_{g2}+K_2 U_{g1}+0=0+K_2\)
\(mgh=\frac{1}{2}mv^2+\frac{1}{2}I\omega ^2\)
For correctly substituting into equation above for both linear and rotational kinetic energy
\(Mgh=\frac{1}{2}M(R\omega )^2+\frac{1}{2}\left ( \frac{MR^2}{2} \right )\omega ^2 gh=\frac{3}{4}R^2\omega ^2 \omega =\sqrt{\frac{4gh}{3R^2}}\)
For correctly substituting into the equation for angular momentum \(L=I\omega =\left ( \frac{MR^2}{2} \right )\left ( \sqrt{\frac{4gh}{3R^2}} =MR\sqrt{\frac{gh}{3}} \right )\)
(b) Selecting “No” For a correct justification Example: The frictional force exerts an external torque on the cylinder therefore the angular momentum of the cylinder is not conserevd. Example: The angular velocity is changing with h; therefore, L is changing.
(c) For setting the total rotational inertia for the toy equal to the sum of the rotaional inertias of the three cylinders \(T_tot=2I_{OUTER}+I_{INNER}=2\frac{MR^2}{2}_{OUTER}+\left ( \frac{MR^2}{2}_{INNER} \right )
I_{tot}=2\left ( \frac{M(2R)^2}{2} \right )+\left ( \frac{MR^2}{2} \right )=4MR^2+\frac{MR^2}{2}
I_{tot}=\frac{9}{2}MR^2\)
(d)i) For correctly drawing a vector representing the normal force perpendicular to the dashed line For correctly drawing a vector representing the weight of the toy directed straight down For correctly drawing a vector representing the frictional force directed up the incline Note: A maximum of two points can be earned if there are any extraneous vectors
ii) For correctly using Newton’s second law in linear form for the toy on the incline
\(F=ma\therefore (3M)g(sin\theta)-F_f=(3M)a
\varsigma =Ia\therefore F_fR=\left ( \frac{9}{2}MR^2 \right )\left ( \frac{a}{R} \right )\therefore F_f=\frac{9}{2}Ma
3Mg(sin\theta)-\frac{9}{2}Ma=3Ma\therefore 3g(sin\theta)=\frac{15}{2}a
a=\frac{2}{5}g(sin\theta)\)
(d) For an answer consistent with part (d)(ii)
iii) \(F_f=\frac{9}{2}M\left ( \frac{2}{5}g(sin\theta) \right )=\frac{9}{5}Mg(sin\theta)\)
(e) For using both rotational and linear kinetic energy for the total kinetic energy of the toy
\(K=K_L+K_R=\frac{1}{2}mv^2+\frac{1}{2}I\omega ^2\)
For correctly substituting for both the rotational inertia, the mass, and \(\omega =v/R\) into the equation above
\(K=\frac{1}{2}(3M)v^2+\frac{1}{2}\left ( \frac{9}{2}MR^2 \right )\omega ^2=\frac{3}{2}Mv^2+\frac{9}{4}MR^2\left ( \frac{v}{R} \right )^2=\frac{15}{4}Mv^2\)
Question
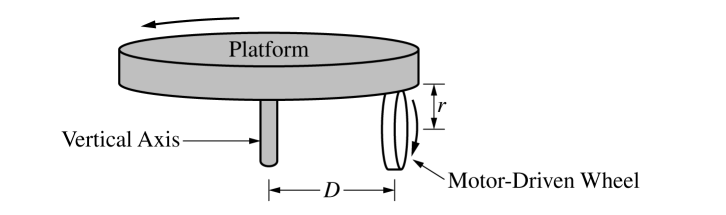
A horizontal circular platform with rotational inertia IP rotates freely without friction on a vertical axis. A small motor-driven wheel that is used to rotate the platform is mounted under the platform and touches it. The wheel has radius r and touches the platform a distance D from the vertical axis of the platform, as shown above. The platform starts at rest, and the wheel exerts a constant horizontal force of magnitude F tangent to the wheel until the platform reaches an angular speed ωP after time Δt . During time Δt , the wheel stays in contact with the
platform without slipping.
(a) Derive an expression for the angular speed ωP of the platform. Express your answer in terms of IP , r, D, F, Δt , and physical constants, as appropriate.
(b) Determine an expression for the kinetic energy of the platform at the moment it reaches angular speed ωP .
Express your answer in terms of IP , r, D, F, Δt , and physical constants, as appropriate.
(c) Derive an expression for the angular speed of the wheel ωW when the platform has reached angular speed ωP . Express your answer in terms of D, r, ωP , and physical constants, as appropriate.
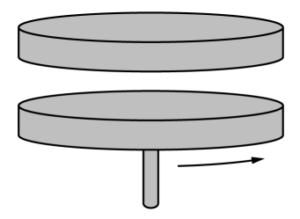
When the platform is spinning at angular speed ωP , the motor-driven wheel is removed. A student holds a disk directly above and concentric with the platform, as shown above. The disk has the same rotational inertia IP as the platform. The student releases the disk from rest, and the disk falls onto the platform. After a short time, the disk and platform are observed to be rotating together at angular speed ωf .
(d) Derive an expression for ωf . Express your answer in terms of ωP , IP , and physical constants, as appropriate.
A student now uses the rotating platform (IP = 3.1 kg•m2 ) to determine the rotational inertia IU of an unknown object about a vertical axis that passes through the object’s center of mass. The platform is rotating at an initial angular speed ωi when the unknown object is dropped with its center of mass directly above the center of the platform. The platform and object are observed to be rotating together at angular speed ωf . Trials are repeated for different values of ωi . A graph of ωif as a function of ωi is shown on the axes below.
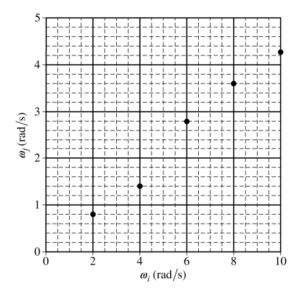
(e)
i. On the graph on the previous page, draw a best-fit line for the data.
ii. Using the straight line, calculate the rotational inertia of the unknown object IU about a vertical axis passing through its center of mass.
(f) The kinetic energy of the spinning platform before the object is dropped on it is Ki . The total kinetic energy of the platform-object system when it reaches angular speed ωf is Kf . Which of the following expressions is true?
____ Kf < Ki ____Ki = Ki ____ Kf > Ki
Justify your answer.
(g) One of the students observes that the center of mass of the object is not actually aligned with the axis of the platform. Is the experimental value of IU obtained in part (e) greater than, less than, or equal to the actual value of the rotational inertia of the unknown object about a vertical axis that passes through its center of mass?
____ Greater than ____ Less than ____ Equal to
Justify your answer.
Answer/Explanation
Ans:
(a)
ωp = O + α (Δt) τnet = Ipα = F•D \(\alpha =\frac{F\cdot D}{I_{p}}\)
\(\omega _{p} = \frac{FD\Delta t}{I _{p}}\) \(\frac{KyM/y\cdot f}{m^{2}\cdot ky}\)
(b)
\(K_{rot} = 1/2 I_{p}{\omega _{p}}^{2}=\frac{I_{p}F^{2}D^{2}\Delta t^{2}}{2{I_{p}}^{2}}=\frac{(FD\Delta t)^{2}}{2I_{p}}\)
(c)
Vp = Vw
ωp • D = ωw • r
ωw = \(\frac{\omega _{p}\cdot D}{r}\)
(d)
Ipωp = 2Ipωf \(\omega _{f} = \frac{\omega _{p}}{2}\)
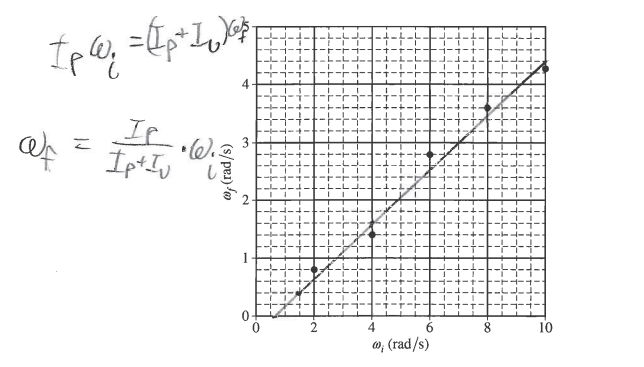
(e)
\(\omega _{f} = \frac{I_{p}}{I_{p}+I_{u}}\cdot \omega _{i}\) \(Slope = \frac{1.2}{2.5}= 0.48\)
\(\omega _{f}(rod/s)= 0.48\cdot \omega _{i}(rod/s)-0.32\)
\(0.48 = \frac{IP}{I_{p}+I_{u}}\) \(0.48I_{p}+0.48I_{u} = I_{p}\)
\(I_{u} = 3.36 kg\cdot m^{2}\)
(f)
X Kf < Ki
Krot = 1/2 Iω2
I increased and ω decreased 24.8 8.2688 liquidly, preserving momentum. The square of ω, however, decreased much more, so Krot decreased.
(g) X Greater than
Iu will be observed to be that of the object when it is some distance t from the contents increasing out perceive value of Iu by about Mx2.
Question
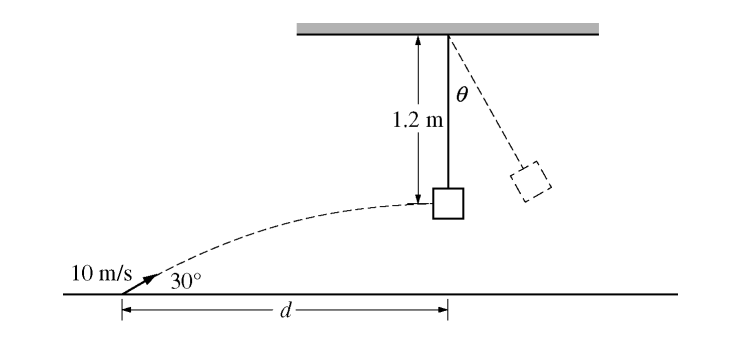
A small dart of mass 0.020 kg is launched at an angle of 30° above the horizontal with an initial speed of 10 m/s. At the moment it reaches the highest point in its path and is moving horizontally, it collides with and sticks to a wooden block of mass 0.10 kg that is suspended at the end of a massless string. The center of mass of the block is 1.2 m below the pivot point of the string. The block and dart then swing up until the string makes an angle θ with the vertical, as shown above. Air resistance is negligible.
(a) Determine the speed of the dart just before it strikes the block.
(b) Calculate the horizontal distance d between the launching point of the dart and a point on the floor directly below the block.
(c) Calculate the speed of the block just after the dart strikes.
(d) Calculate the angle θ through which the dart and block on the string will rise before coming momentarily to rest.
(e) The block then continues to swing as a simple pendulum. Calculate the time between when the dart collides with the block and when the block first returns to its original position.
(f) In a second experiment, a dart with more mass is launched at the same speed and angle. The dart collides with and sticks to the same wooden block.
i. Would the angle θ that the dart and block swing to increase, decrease, or stay the same?
_____ Increase _____ Decrease _____ Stay the same
Justify your answer.
ii. Would the period of oscillation after the collision increase, decrease, or stay the same?
_____ Increase _____ Decrease _____ Stay the same
Justify your answer.
Answer/Explanation
Ans:
(a)
Vtop = ?
Vtop, y = O m/s because top of protectory
Vtop,x only speed: Vo cosθ = 10 m/s (Cos 300) = 8,66 m/s
(b)
d = ? Vtop, y = O, V0, y = V0sin 300
d = Vx (t) \(\frac{V_{0}y}{g}=t\)
d = 8.66 m/s × 0.51s \(t = \frac{V_{0}sin30^{0}}{g}=0.51s\)
(c)
Vblock = ?
Cons. of angular momentum:
Li = Lf
rmv = Iw, \(w = \frac{v}{r}\) M = mdart + Mblock
\(rmv = MR^{2}(\frac{V}{R})\)
mdart (V0) = mdart + Mblock) (Vt)
10 m/s (OtoZ) = (0.oz + 0.1) (Vf)
Vf = 1.67 m/s
(d)
θ = ?
\(\frac{1}{2}mv^{2}=mgh\)
\(\frac{1}{2}(V_{f})^{2}=gh\) \(\frac{1}{2}(1.67 m/s)^{2}=9.81 m/s (h)\)
h = 0.14 m
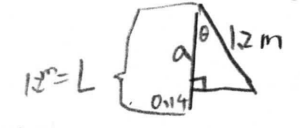
\(cos\theta = \frac{a}{L}\)
\(cos\theta = \frac{1.2 m – h}{1.2 m}\)
\(cos\theta = \frac{1.2 – 0.14m}{1.2 m}\)
\(\theta = 28.2^{0}\)
(e)
Time = T/2
\(T = 2\pi \sqrt{\frac{L}{q}} \) simple pendulum
\(\frac{T}{2} = \pi \sqrt{\frac{L}{q}} \)
\(\frac{T}{2} = \pi \sqrt{\frac{1.2}{9.81}} \Rightarrow T/2 = 1.15\)
(f) i.
x Decrease
because the final velocity would be less and thus answer angle;
ii. x Stay the same
\(T = 2\pi \sqrt{\frac{L}{g} }\) the period would stay the same because the length and a stays the same despite change in mass
