Question
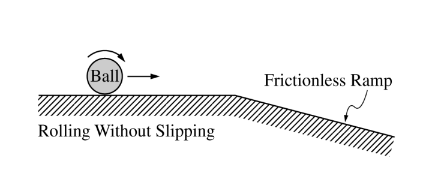
A ball, rolling without slipping on a horizontal surface, encounters a frictionless, downward- sloping ramp, as shown above. Which of the following correctly describes the motion of the ball on the ramp?
(A) Constant translational speed with no angular speed
(B) Increasing translational speed with no angular speed
(C) Increasing translational speed with constant nonzero angular speed
(D) Increasing translational speed with decreasing angular speed
(E) Increasing translational speed with increasing angular speed
Answer/Explanation
Question
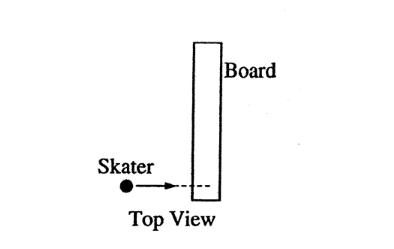
A long board is free to slide on a sheet of frictionless ice. As shown in the top view above, a skater skates to the board and hops onto one end, causing the board to slide and rotate. In this situation, which of the following occurs?
(A) Linear momentum is converted to angular momentum.
(B) Kinetic energy is converted to angular momentum.
(C) Rotational kinetic energy is conserved.
(D) Translational kinetic energy is conserved.
(E) Linear momentum and angular momentum are both conserved.
Answer/Explanation
Question
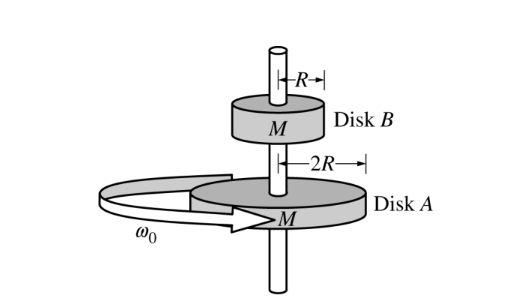
Two horizontal disks of mass M have the radii shown above. Disk A is attached to an axle of negligible mass spinning freely with angular velocity\( ω_0\) . Disk B, not attached to the axle and initially held at rest, is released and drops down onto disk A. When both disks spin together without slipping, the angular velocity \(ω_f\) of the disks is
(A)\(\frac{1}{3}\omega _0\)
(B)\(\frac{1}{2}\omega _0\)
(C)\(\frac{2}{3}\omega _0\)
(D)\(\frac{4}{5}\omega _0\)
(E)\(\frac{2}{\sqrt{5}}\omega _0\)
Answer/Explanation
Ans:D
Substituting into the equation for conservation of angular momentum yields
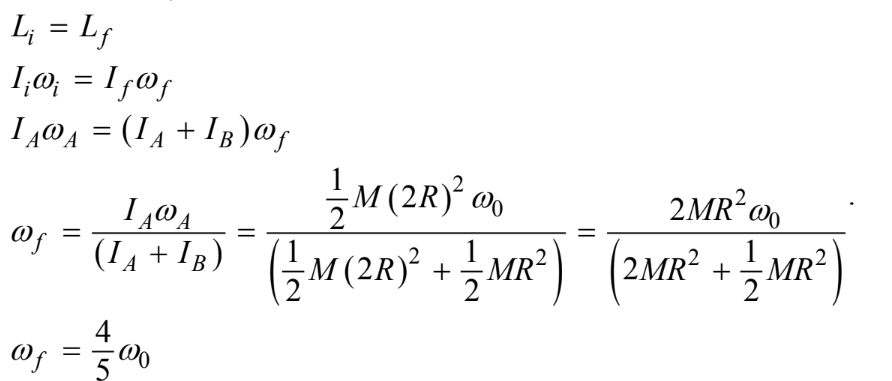
Question
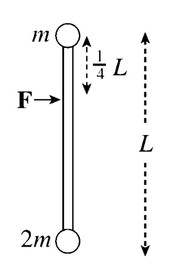
The figure shows a view from above of two objects attached to the end of a rigid massless rod at rest on a frictionless table. When a force F is applied as shown, the resulting rotational acceleration
of the rod about its center of mass is kF/(mL). What is k?
(A) \(\frac{3}{8}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{5}{8}\)
(D) \(\frac{3}{4}\)
(E) \(\frac{5}{6}\)
Answer/Explanation
Ans: C
The center of mass of the system is at a distance of
\(y_{cm}=\frac{(m)(0) + (2m)(L)}{m +2m} = \frac{2}{3} L\)
below the mass m. With respect to this point, the clockwise torque produced by the force F has magnitude
\(\tau = rF = (\frac{2}{3}L – \frac{1}{4} L) F = \frac{5}{12} LF\)
Since the rotational inertia of the system about its center of mass is
\(I = \sum m_i r_i^2 = m (\frac{2}{3}L)^2 + (2m) (\frac{1}{3}L)^2 = \frac{2}{3} mL^2\)
the equation \(\tau = Ia\) becomes
Question
What is the fewest number of the following conditions to ensure that angular momentum is conserved?
I. Conservation of linear momentum
II. Zero net external force
III. Zero net external torque
(A) II only
(B) III only
( C) I and II only
(D) I and III only
(E) II and III only
Answer/Explanation
Ans: B
