How is angular momentum related to linear momentum?
▪ The angular momentum, 𝐿⃗ , of a particle about an axis perpendicular to the plane of the particles motion:
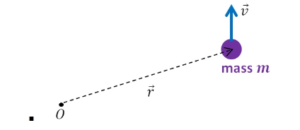
An object moving linearly through space can also have angular momentum about some reference point.
For point mass moving linear, its angular moment a distance r away along a perpendicular axis is given:
𝑳 = 𝒎𝒗𝒓
▪ Angular momentum is a vector quantity. The direction is clockwise (–) or counterclockwise (+).
▪ For an object consisting of many particles, the total angular momentum is found by adding up the angular momenta of all particles in the object:
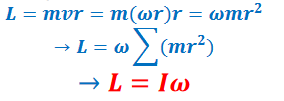
▪ The Impulse–Momentum Theorem for Rotation:
Angular Impulse – 𝐽𝜃 = 𝜏𝑡
A torque applied for a time changes angular momentum:
𝜏𝑡 = 𝐼𝜔𝑓 − 𝐼𝜔𝑖
→ 𝑱𝜽 = ∆𝑳
Apply the impulse momentum theorem for momentum.
Example A: A 3.0 kg particle moves parallel to the x–axis along the line 𝑦 = 2.0 m with velocity 2.0 m/s. What is the angular momentum of the particle when it is 4.0 m to the left of the origin?
Answer/Explanation
Ans: 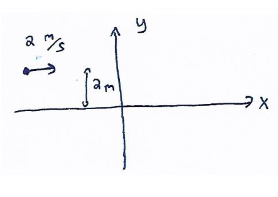
L = mvr = (3 kg) (2 m/s) (2m)
L = 12 kg m/s2
Example B: The angular speed of a flywheel having a rotational inertia of 0.150 kg∙m2 about its central axis decreases from 20.0 rad/s to 4.00 rad/s in 1.50 s. What is the magnitude of the average torque acting on the flywheel about its central axis during this period?
Answer/Explanation
Ans: JΘ = ΔL
⇒τt = Iωf – Iωi ⇒ τ = \(\frac{I\omega _{f}-I_{\omega i}}{t}\)
⇒τ= \(\frac{(.15 Kg m^{2})(4 rad/s)-(.15 Kg m^{2})(20 rad/s)}{1.5 s}=-1.6 Nm\)
Apply conservation of momentum in rotation.
▪ Suppose two spinning disks on axle slide together. The disks collide and exert impulses on each other. By Newton’s 3rd Law, the impulses are equal but opposite:
𝜏𝐴 𝑜𝑛 𝐵 = 𝜏𝐵 𝑜𝑛 𝐴
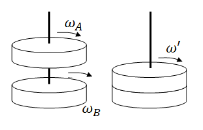
▪ Since all torques are internal, and no external torques act, momentum must be constant:
If there are no external torques applied, the initial angular momentum of a system will be equal to the final angular momentum of the system:
𝐿𝑖 = 𝐿𝑓
▪ Internal interaction in a system cannot change the total angular momentum of the system.
▪ Example: Skaters move faster when pulling in their arms as this decreases their moment of inertia, allow their angular speed to increase without any external force.
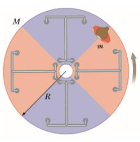
Example C: A circular disc platform rotates about a central axis. The platform has a mass M and a radius R. A student of mass M/4 walks slowly from the rim of the disk toward its center. If the angular speed of the system is 𝜔 when the student is at the rim, what is the angular speed when she reaches a point R/2 from the center?
Answer/Explanation
Ans: Li = Lf
\(\left ( \frac{1}{2}MR^{2}+\frac{M}{4}R^{2} \right )\omega =(\frac{1}{2}MR^{2}+\frac{M}{4}\left ( \frac{R}{2} \right )^{2})\omega _{f}\)
\(\frac{3}{4}MR^{2}\omega =\frac{9}{16}MR^{2}\omega _{f}\)
\(\omega _{f}=\frac{4}{3}\omega \)
Example D: A bullet of mass m is shot at speed v into a block of mass M. The bullet hits a distance of r from the center of the block as shown (the block is of width 2r). The block flies into the air while spinning.
a) Calculate the angular speed of the block.
Answer/Explanation
Ans: 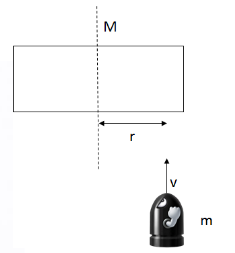
Li = Lf
mvr = (Iblock + Ibullet) ω
\(mvr=(\frac{1}{12}M(2r)^{2}+mr^{2})\omega \)
\(\Rightarrow \omega =\frac{mvr}{\frac{1}{3}Mr^{2}+mr^{2}}=\frac{3mvr}{Mr^{2}+3mr^{2}}\)
b) How would the maximum height reached by the block compare if the bullet was shot directly into the center of the block?
Answer/Explanation
Ans: In a collision where angular moment is present, angular momentum is conserved. If linear momentum is also present, it will also be conserved. These two will be conserved separately. No matter where the bullet hits the block, the linear speed after the collision will be given by:
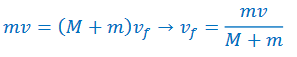
In both cases, the bullet/block combo will have the same linear speed after the collision and will reach the same height, even though the block will spin in one case and will not spin in the other.
