Question

A block of mass m starts at rest at the top of an inclined plane of height h, as shown in the figure above. The block travels down the inclined plane and makes a smooth transition onto a horizontal surface. While traveling on the horizontal surface, the block collides with and attaches to an ideal spring of spring constant k. There is negligible friction between the block and both the inclined plane and the horizontal surface, and the spring has negligible mass. Express all algebraic answers for parts (a), (b), and (c) in terms of m, h, k, and physical constants, as appropriate.
(a)
i. Derive an expression for the speed of the block just before it collides with the spring.
ii. Is the speed halfway down the incline greater than, less than, or equal to one-half the speed at the bottom of the inclined plane?
____ Greater than _____ Less than ____ Equal to
Justify your answer.
(b) Derive an expression for the maximum compression of the spring.
(c) Determine an expression for the time from when the block collides with the spring to when the spring reaches its maximum compression.
The block is again released from rest at the top of the incline, and when it reaches the horizontal surface it is moving with speed v0 . Now suppose the block experiences a resistive force as it slides on the horizontal surface.
The magnitude of the resistive force F is given as a function of speed v by F = βb2 , where β is a positive constant with units of kg/m .
(d)
i. Write, but do NOT solve, a differential equation for the speed of the block on the horizontal surface as a function of time t before it reaches the spring. Express your answer in terms of m, h, k, β, v, and physical constants, as appropriate.
ii. Using the differential equation from part (d)i, show that the speed of the block v(t) as a function of time t can be written in the form \(\frac{1}{v(t)}=\frac{1}{v_{0}}+\frac{\beta t}{m}\) , where 0v is the speed at t = 0.
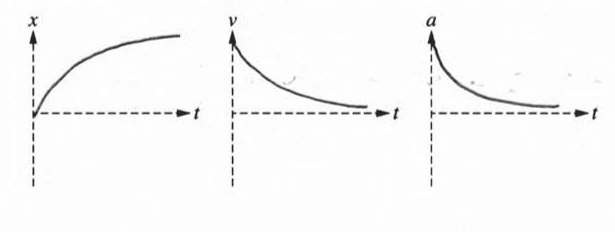
(e) Sketch graphs of position x as a function of time t, velocity v as a function of time t, and acceleration a as a function of time t for the block as it is moving on the horizontal surface before it reaches the spring.
Answer/Explanation
Ans:

(a) i.
\(\frac{1}{2}MV^{2}=mgh \rightarrow v = \sqrt{2gh}\)
ii.
√ Greater than
\(mg\left ( \frac{1}{2}h \right )=\frac{1}{2}MV^{2}\)
\(V = \sqrt{gh}\rightarrow \sqrt{gh} \) is greater than \(\frac{1}{2} \sqrt{2gh} \)
(b)
\(mgh =\frac{1}{2} KX^{2}\)
\(\frac{2mgh}{k}=X^{2} \rightarrow X = \sqrt{\frac{2mgh}{k}}\)
(c)
\(T = 2\pi \sqrt{\frac{M}{k}}\)
↓
\(\frac{1}{4}T = \frac{1}{2}\pi \sqrt{\frac{M}{k}}\)
(d) i.
∑F = ma
\(-Bv^{2}= m\frac{dv}{dt}\)
\(\frac{dv}{dt}=\frac{-B}{m}v^{2}\)
ii.
\(\int_{V_{0}}^{V}\frac{1}{V^{2}}dV = \int_{0}^{t}-\frac{B}{m}dt\)
\(\left [ \frac{-1}{V} \right ]_{v}^{v_{0}} = \frac{-Bt}{m}\)
\(\frac{1}{V(t)}=\frac{1}{V_{0}}+ \frac{Bt}{m}\)
(e)
Question
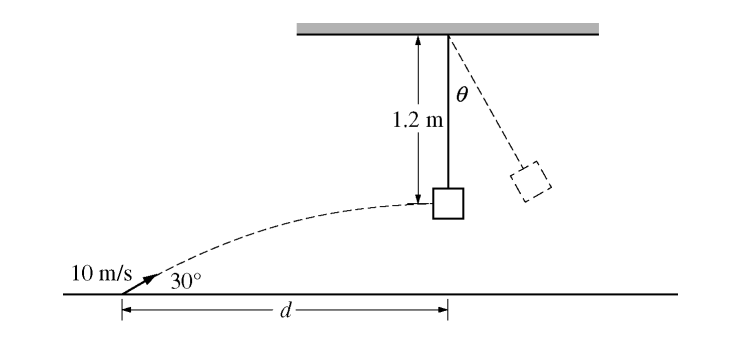
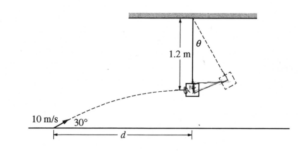
A small dart of mass 0.020 kg is launched at an angle of 30° above the horizontal with an initial speed of 10 m/s. At the moment it reaches the highest point in its path and is moving horizontally, it collides with and sticks to a wooden block of mass 0.10 kg that is suspended at the end of a massless string. The center of mass of the block is 1.2 m below the pivot point of the string. The block and dart then swing up until the string makes an angle θ with the vertical, as shown above. Air resistance is negligible.
(a) Determine the speed of the dart just before it strikes the block.
(b) Calculate the horizontal distance d between the launching point of the dart and a point on the floor directly below the block.
(c) Calculate the speed of the block just after the dart strikes.
(d) Calculate the angle θ through which the dart and block on the string will rise before coming momentarily to rest.
(e) The block then continues to swing as a simple pendulum. Calculate the time between when the dart collides with the block and when the block first returns to its original position.
(f) In a second experiment, a dart with more mass is launched at the same speed and angle. The dart collides with and sticks to the same wooden block.
i. Would the angle θ that the dart and block swing to increase, decrease, or stay the same?
_____ Increase _____ Decrease _____ Stay the same
Justify your answer.
ii. Would the period of oscillation after the collision increase, decrease, or stay the same?
_____ Increase _____ Decrease _____ Stay the same
Justify your answer.
Answer/Explanation
Ans:
(a)
Vtop = ?
Vtop, y = O m/s because top of protectory
Vtop,x only speed: Vo cosθ = 10 m/s (Cos 300) = 8,66 m/s
(b)
d = ? Vtop, y = O, V0, y = V0sin 300
d = Vx (t) \(\frac{V_{0}y}{g}=t\)
d = 8.66 m/s × 0.51s \(t = \frac{V_{0}sin30^{0}}{g}=0.51s\)
(c)
Vblock = ?
Cons. of angular momentum:
Li = Lf
rmv = Iw, \(w = \frac{v}{r}\) M = mdart + Mblock
\(rmv = MR^{2}(\frac{V}{R})\)
mdart (V0) = mdart + Mblock) (Vt)
10 m/s (OtoZ) = (0.oz + 0.1) (Vf)
Vf = 1.67 m/s
(d)
θ = ?
\(\frac{1}{2}mv^{2}=mgh\)
\(\frac{1}{2}(V_{f})^{2}=gh\) \(\frac{1}{2}(1.67 m/s)^{2}=9.81 m/s (h)\)
h = 0.14 m
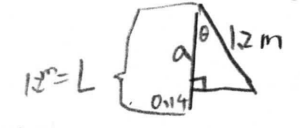
\(cos\theta = \frac{a}{L}\)
\(cos\theta = \frac{1.2 m – h}{1.2 m}\)
\(cos\theta = \frac{1.2 – 0.14m}{1.2 m}\)
\(\theta = 28.2^{0}\)
(e)
Time = T/2
\(T = 2\pi \sqrt{\frac{L}{q}} \) simple pendulum
\(\frac{T}{2} = \pi \sqrt{\frac{L}{q}} \)
\(\frac{T}{2} = \pi \sqrt{\frac{1.2}{9.81}} \Rightarrow T/2 = 1.15\)
(f) i.
x Decrease
because the final velocity would be less and thus answer angle;
ii. x Stay the same
\(T = 2\pi \sqrt{\frac{L}{g} }\) the period would stay the same because the length and a stays the same despite change in mass
Question
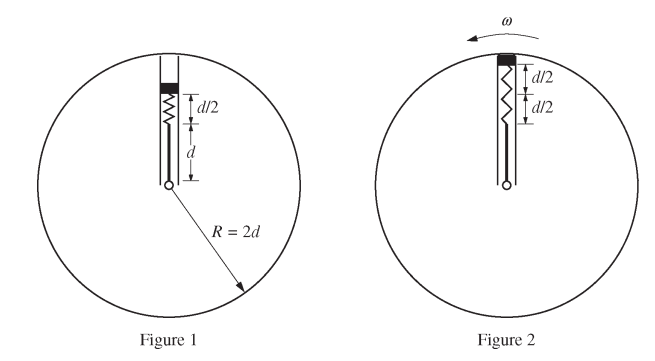
A uniform rod of length d has one end fixed to the central axis of a horizontal, frictionless circular platform of radius R = 2d . Fixed at the other end of the rod is an ideal spring of negligible mass to which a block is attached. The block is set in frictionless grooves so that it can only move along a radius of the platform, as shown in Figure 1 above. The equilibrium length of the spring is d/2 . Below is a table showing the mass of the block and the masses and rotational inertias of the rod and platform.
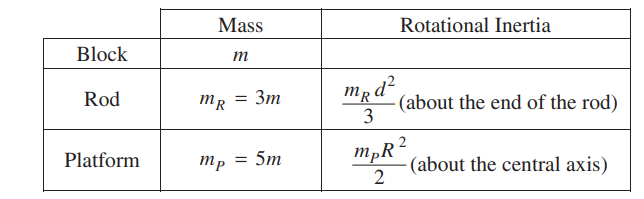
A motor begins to slowly rotate the platform counterclockwise as viewed from above until the platform reaches a constant angular speed ω . Under these conditions, the spring has stretched by an additional length d/2 , as shown in Figure 2.
Answer the following questions for the platform rotating at constant angular speed ω . Express all algebraic answers in terms of m, d, ω , and physical constants, as appropriate.
(a) Derive an expression for the spring constant of the spring.
(b)
i. Determine an expression for the rotational inertia of the block around the axis of the platform.
ii. Derive an expression for the rotational inertia of the entire system about the axis of the platform.
(c) Determine an expression for the angular momentum of the entire system about the axis of the platform
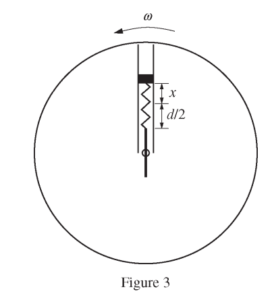
While the system continues to rotate, a small mechanism in the pivot moves the rod slowly until the center of the rod is positioned on the axis, as shown in Figure 3 above. The same constant angular speed ω is maintained by the motor driving the platform.
(d) Derive an expression for the distance x that the spring is stretched when the rod reaches the position shown in Figure 3 above.
For parts (e), (f), and (g), assume the center of the rod is still moving toward the axis of the platform.
(e) Is the angular momentum of the entire system increasing, decreasing, or staying the same?
_____Increasing _____Decreasing _____Staying the same
Justify your answer.
(f) In order to keep the system rotating with constant angular speed ω , is the motor doing positive work, negative work, or no work on the rotating system?
_____Positive _____Negative _____No work
Justify your answer.
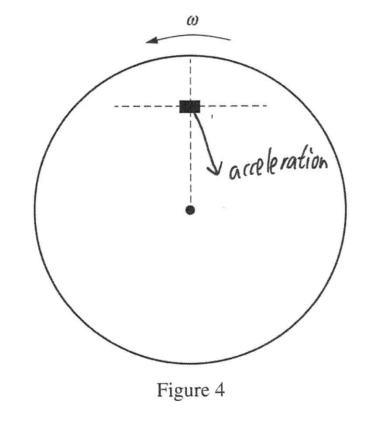
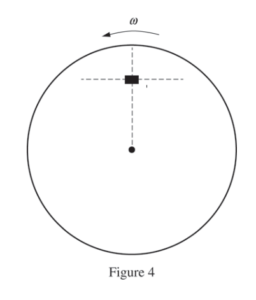
(g) On the block in Figure 4 below, draw a single vector representing the direction of the acceleration of the block. Draw the vector so that it is starting on, and pointing away from, the block.
Answer/Explanation
Ans:
(a)
Since Fspring = Fcentripetal,
\(\frac{kd}{2}= mw^{2}(d + \frac{d}{2}+\frac{d}{2})\)
So \(\frac{kd}{2}= 2mdw^{2}\)
So k = 4mw2
(b) i.
\(I = mr^{2}= m(d + \frac{d}{2}+\frac{d}{2})^{2}=4md^{2}\)
ii.
Isys = Iblock + I rod + Iplatform
\(= 4md^{2}+\frac{3md^{2}}{3}+\frac{5m(2d)^{2}}{2}\)
= 4md2 + md2 + 10md2
= 15 md2
(c)
L = Iw = 15 md2w
(d)
Since Fspring = Fcentripetal,
\(kx = mw^{2}\left ( \frac{d}{2}+\frac{d}{2}+x \right )\)
So 4mw2x = mw2 (d+x)
So d + x = 4x
So 3x = d
So X = d/3
(e)
√ Decreasing
By parallel – axis thebrem, we know that the closer the center of mass of an objet is to the rotational axis, the lower the rotational inertia is. Since the rod takes the rod and the block closer to the center, their intertia decreases. Since w stay the same, L = Iw will decrease.
(f)
√ Negative
If there were no motor, by conservation of angular momentum, Since I decreased, w will increase. So in order to maintain constant w, the motor have to do negative workto slow down the angular speed.
(g)