Question
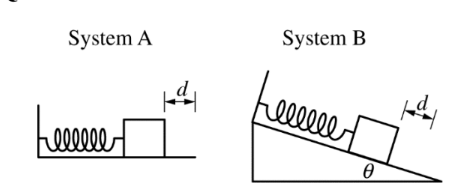
Systems A and B contain identical ideal springs and identical blocks that can slide along a surface of negligible friction. In system A, the surface is horizontal. In system B, the surface makes an
angle q with the horizontal. Initially, both blocks are at rest and in equilibrium. Each block is then pulled the same distance d in the direction shown in the figures and released from rest at t = 0.
After the block in system A is released from rest, the time for the block to first reach a maximum speed is\( \Delta t_A\). After the block in system B is released, the time for the block to first reach a maximum speed is
(A) \( \Delta t_A\)
(B) \(\Delta t_A\) (sin \theta)\)
(C) \(\Delta t_A\) (sin \theta)\)
(D)\(\Delta t_A\) (cos \theta)\)
(E) \(\Delta t_A\) (cos\theta)\)
Answer/Explanation
Ans:A
Question

Systems A and B contain identical ideal springs and identical blocks that can slide along a surface of negligible friction. In system A, the surface is horizontal. In system B, the surface makes an
angle q with the horizontal. Initially, both blocks are at rest and in equilibrium. Each block is then pulled the same distance d in the direction shown in the figures and released from rest at t = 0.
For system A, when the block is halfway between its release position and its equilibrium position, the block’s kinetic energy is K and the elastic potential energy of the spring-block system is U.
The ratio \(K/ U\) is
(A) 1/ 3
(B) 1/ 2
(C) 1/ 1
(D) 2/ 1
(E) 3/ 1
Answer/Explanation
Ans:E
The total mechanical energy of the system is the sum of the elastic potential energy of the spring-block system and the kinetic energy of the block. When the block is at its maximum displacement, the kinetic energy is zero and all the energy is elastic potential energy. Substituting into the equation for elastic potential energy yields\( E=U_S{max}=\frac{1}{2}kx^2_{max}= =\frac{1}{2}kd^2\) Substituting into the equation for the elastic potential energy equation when the block is halfway from its maximum displacement yields \(U_S=\frac{1}{2}k (\frac{1}{2}d)^2==\frac{1}{8}kd^2\) Substituting into conservation of energy to calculate the kinetic energy of the block yields\( E=U_S+K\) \(U_S=\frac{1}{2}kd^2= (\frac{1}{8}kd)^2+K
\(K=\frac{3}{8}kd^2\) thus, the ratio of the kinetic energy to the elastic potential energy is
Question

Systems A and B contain identical ideal springs and identical blocks that can slide along a surface of negligible friction. In system A, the surface is horizontal. In system B, the surface makes an
angle q with the horizontal. Initially, both blocks are at rest and in equilibrium. Each block is then pulled the same distance d in the direction shown in the figures and released from rest at t = 0.
A student wants to use an apparatus similar to system B to measure the acceleration due to gravity g. If the mass of the block, the force constant of the spring, and the angle of the incline are known, what additional data must be measured to determine an experimental value for g ?
I. The stretch of the spring at the equilibrium position
II. The speed of the block as it passes the equilibrium position
III. The time interval between two consecutive passes through the equilibrium position
(A) I only
(B) II only
(C) I and II
(D) II and III
(E) I and III
Answer/Explanation
Ans:A
Substitution into a Newton’s second law equation for the \(F_{net}=0=F_s-W sin\theta\) block at equilibrium in system B yields \( k(\Delta x) =msin\theta\)
Question
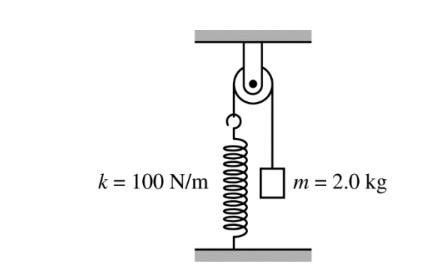
A 2.0 kg block is attached to a string that passes over a pulley and is attached to an ideal spring of spring constant k = 100 N m, as shown above. The pulley and string have negligible mass, and there is negligible friction in the pulley. The block is held in place with the spring at its original unstretched length and then released from rest. The amplitude of the resulting oscillation is most nearly
(A) 4.0 cm
(B) 2.0 cm
(C) 10 cm
(D) 20 cm
(E) 40 cm
Answer/Explanation
Ans:D
The spring begins unstretched. To determine the amplitude of oscillation, Newton’s second law can be used to determine how far the block will now stretch the spring to the equilibrium position. Substituting into Newton’s second law yields
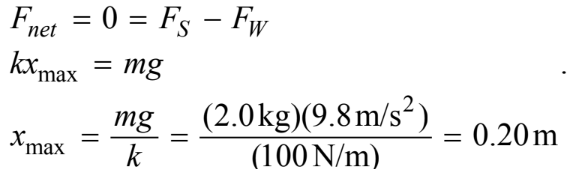
Question
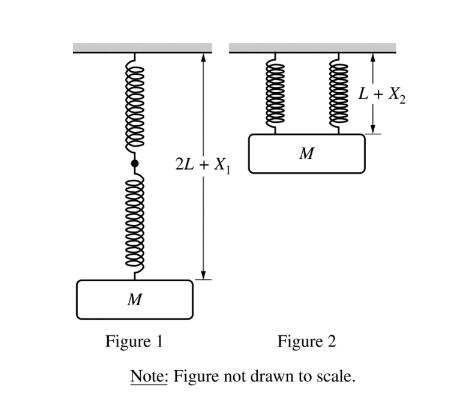
A block of mass M is suspended from two identical springs of negligible mass, spring constant kand unstretched length L. First, one spring is attached to the end of the other spring.
The block is then attached to the end of the second spring and slowly lowered to its equilibrium position. The two springs stretch a total distance of \(X_1\) , as shown in Figure 1 above. Next, the springs are hung side by side. The block is attached to the end of the springs and again slowly lowered to its equilibrium position. The springs each stretch a distance of \(X_2\) , as shown
in Figure 2 above. Which of the following equations correctly shows the relationship between \(X_1\) and \(X_2\) ?
(A)\(X_1=X_2\)
(B)\(X_1=\sqrt{2X_2}\)
(C)\(X_1=2X_2\)
(D)\(X_1=4X_2\)
(E)\(X_1=8X_2\)
