Question
Two moons of equal mass are in circular orbits around a planet. Moon 1 orbits with a radius of r and moon 2 orbits with a radius of 3r. What is the ratio of the magnitude of the planet’s gravitational force on moon 2 to that on moon 1, \(F_{G(on2)}/F_{G(0n1)}\) ?
(A) 9/1
(B) 3/ 1
(C) 1/1
(D) 1/ 3
(E) 1/ 9
Answer/Explanation
Question
The escape speed for a rocket at Earth’s surface is \(v_e\). What would be the rocket’s escape speed from the surface of a planet with twice Earth’s mass and the same radius as Earth?
(A)\(2v_e\)
(B)\(\sqrt{2v_e}\)
(C)\(v_e\)
(D)\(\frac{v_e}{\sqrt{2}}\)
(E)\(\frac{v_e}{2}\)
Answer/Explanation
Question
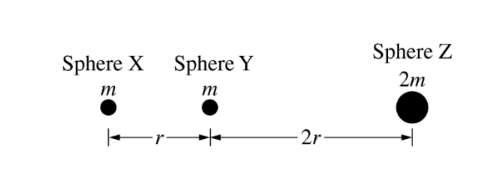
26. Spheres X, Y, and Z have the masses and locations indicated in the figure above. What is the magnitude of the net gravitational force on sphere X due to the other two spheres?
(A)\(\frac{Gm^2}{2r^2}\)
(B)\(\frac{Gm^2}{r^2}\)
(C)\(\frac{11Gm^2}{9r^2}\)
(D)\(\frac{5Gm^2}{4r^2}\)
(E)\(\frac{2Gm^2}{r^2}\)
Answer/Explanation
Ans:C
Both sphere Y and Z will attract sphere X to the right. Adding the force of gravity from both spheres together and substituting into the equation for gravitational force yields
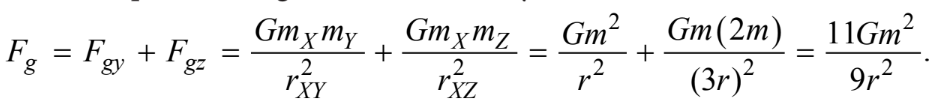
Questions (a)-(b)
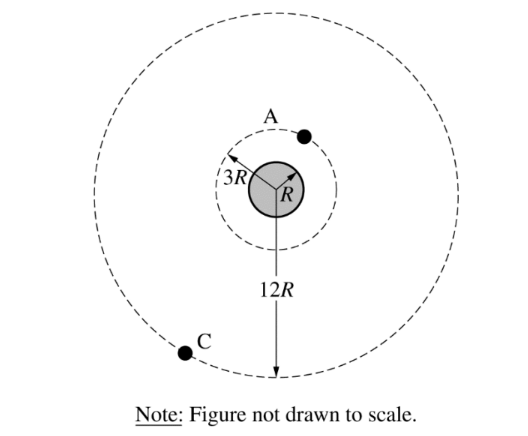
Two identical satellites orbit a planet of radius R in circular orbits A and C of radii 3R and 12R, respectively, as shown above.
Question(a)
How does the magnitude of the gravitational force \(F_A\) between the planet and satellite in orbit A compare to the magnitude of the gravitational force\( F_C\) between the planet and satellite in orbit C?
(A) \(F_A = 2F_C \)
(B) \(F _A= 3F_C \)
(C)\( F_A = 4F_C \)
(D) \(F_ A = 12F_C\)
(E) \(F_ A = 16F_C\)
Answer/Explanation
Ans:E
Substituting into the equation for the gravitational force on the satellite in orbit A yields 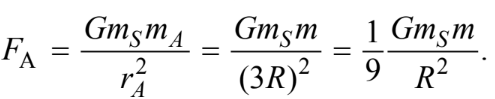
Substituting into the equation for the gravitational force on the
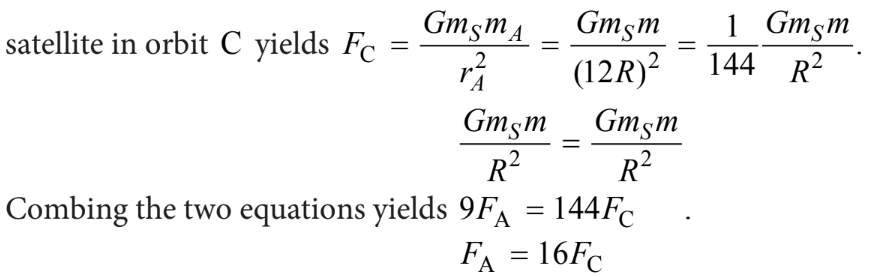
Question(b)
The speed of the satellite in orbit A is \(v_A\) . The speed of the satellite in orbit C is \(v_C\). The ratio \(v_A/ v_C\) is
(A) 1 /2
(B) 1/1
(C) 2/1
(D) 4/1
(E)12/ 1
Answer/Explanation
Ans:C
Setting the centripetal force equal to the gravitational force\( F_c=F_g\)
and solving for the speed of satellite A yields \(\frac{m_Av^2_A}{r_A}=\frac{GMm_A}{r^2_A}\)
\(v_A=\frac{GM}{r_A}\)
\(F_C=F_g\)
Repeating for satellite C yields\( \frac{m_Av^2_A}{r_A}=\frac{GMm_A}{r^2_c}
