Question
A block of mass 3 kg is at rest on a rough plane inclined at 60Å to the horizontal. A force of magnitude 15 N acting up a line of greatest slope of the plane is just sufficient to prevent the block from sliding down the plane.
(i) Find the coefficient of friction between the block and the plane.
The force of magnitude 15 N is now replaced by a force of magnitude X N acting up the line of greatest slope.
(ii) Find the greatest value of X for which the block does not move.
Answer/Explanation
(i) R = 3 g cos 60
Use F = μR
[3gsin 60–μ3gcos60– 15= 0]
μ= 0.732
(ii) [Maximum force =3gsin60+ F= 3 sin60+μ3gcos60]
X= 37(.0)
Question
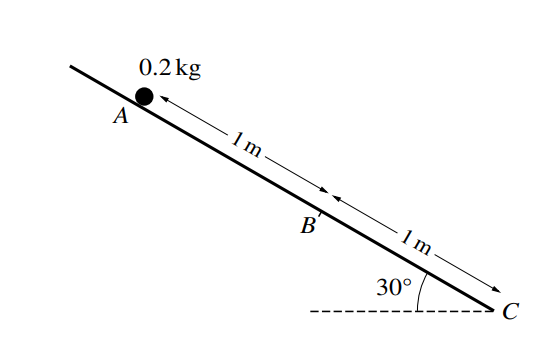
Three points A, B and C lie on a line of greatest slope of a plane inclined at an angle of 30Å to the horizontal, with AB = 1 m and BC = 1 m, as shown in the diagram. A particle of mass 0.2 kg is
released from rest at A and slides down the plane. The part of the plane from A to B is smooth. The part of the plane from B to C is rough, with coefficient of friction – between the plane and the particle.
(a) Given that \(\mu =\frac{1}{2}\sqrt{3}\), find the speed of the particle at C.
(b) Given instead that the particle comes to rest at C, find the exact value of \( \mu\)
Answer/Explanation
(a) \(0.2\times 10\times 0.5=\frac{1}{2}\times 0.2\times v^{2}_{B}\)
\(v^{2}_{B}=10\)
Alternative method for the first 3 marks
0.2 × 10 × sin 30 = 0.2a, a = 5
\(v^{2}_{B}=0^{2}+2\times 5\times 1\)
\(v^{2}_{B}=10\)
(a) THEN, either this method for the next 5 marks
\(R=0.2\times 10\times \cos 30=\sqrt{3}\)
\(F=\frac{\sqrt{3}}{2}\times 0.2\times \frac{\sqrt{3}}{2}\times 10=1.5\)
PE loss = 0.2 × 10 × 0.5 = 1
WD against F = 1.5 × 1
\(\frac{1}{2}0.2\times 10+0.2\times 10\times 0.5=1.5\times 1+\frac{1}{2}0.2v^{2}_{C}\)
\(V_{c}=\sqrt{5}=2.24ms^{-1}\)
OR, this method for the next 5 marks
\(R=0.2\times 10\times \cos 30=\sqrt{3}\)
\(F=\frac{\sqrt{3}}{2}\times 0.2\times \frac{\sqrt{3}}{2}\times 10=1.5\)
0.2 × 10 sin 30 – 1.5 = 0.2a a = –2.5
\(V^{2}_{c}=10+2\times -2.5\times 1\)
\(V_{c}=\sqrt{5}=2.24ms^{-1}\)
(a) Alternative method for question (a)
PE loss = 0.2 × 10 × 2 sin 30 = 2
\(KE\ gain \ =\frac{1}{2}\times 0.2\times v^{2}_{c}\)
Both PE loss and KE gain correct
\(R=0.2\times 10\times \cos 30=\sqrt{3}\)
\(F=\frac{\sqrt{3}}{2}\times 0.2\times \frac{\sqrt{3}}{2}\times 10=1.5\)
WD against F = 1.5 × 1
\(0.2\times 10\times 1=1.5\times 1+\frac{1}{2}\times 0.2\times v^{2}_{C}\)
\(V_{c}=\sqrt{5}=2.24ms^{-1}\)
(b) 0 = 10 + 2a [a = –5]
0.2 × 10 × sin 30 – F = 0.2 × -5
\(2=\mu \sqrt{3}\)
\(\mu= \frac{2}{\sqrt{3}}\)
Alternative method for question (b)
PE loss = 0.2 × 10 × 1 sin 30 = 1
1 + ½ × 0.2 × 10 = F × 1
\(F=\mu \sqrt{3}\)
\(\mu =\frac{2}{\sqrt{3}}\)
(b) Alternative method for question (b)
PE loss = 0.2 × 10 × 2 sin 30 = 2
2 = F × 1
\(F=\mu \sqrt{3}\)
\(\mu=\frac{2}{\sqrt{3}}\)
Question
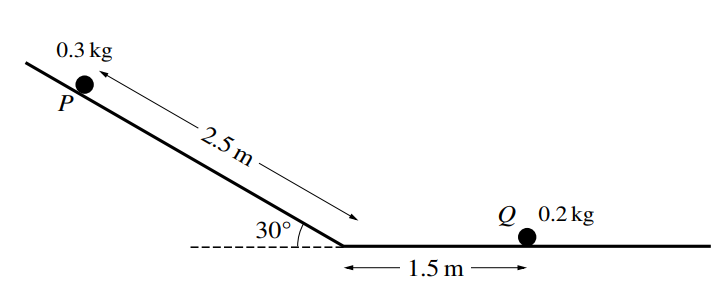
A particle P of mass 0.3 kg, lying on a smooth plane inclined at 30o to the horizontal, is released from rest. P slides down the plane for a distance of 2.5 m and then reaches a horizontal plane. There is no change in speed when P reaches the horizontal plane. A particle Q of mass 0.2 kg lies at rest on the
horizontal plane 1.5 m from the end of the inclined plane (see diagram). P collides directly with Q.
(a) It is given that the horizontal plane is smooth and that, after the collision, P continues moving in the same direction, with speed 2 m s−1.
Find the speed of Q after the collision.
(b) It is given instead that the horizontal plane is rough and that when P and Q collide, they coalesce and move with speed 1.2 m s−1.
Find the coefficient of friction between P and the horizontal plane.
Answer/Explanation
(a) 0.3gsin 30 = 0.3a (a = 5)
(M1 for applying Newton’s second law parallel to the plane)
v2 = 0 + 2 × 2.5 × a
v = 5
0.3 × 5 + 0 = 0.3 × 2 + 0.2 w
Velocity of Q = 4.5 ms–1
(b) 0.3 × z + 0 = 0.5 × 1.2
Velocity of P before collision z = 2 A1
Friction force on P after reaches horizontal plane F = μ × 0.3 g
\(\mu \times 0.3\times 1.5=\frac{1}{2}\times 0.3\times 5^{2}-\frac{1}{2}\times0.3 \times 2^{2} \)
Coefficient μ = 0.7
Alternative method for question (b)
0.3 × z + 0 = 0.5 × 1.2
Velocity of P before collision z = 2
Friction force on P after reaches horizontal plane F = μ × 0.3g
a = (52 –22) / (2 × 1.5) = 7, F = 0.3 × 7
Coefficient μ = 0.7
Question
A particle P of mass 0.4kg is on a rough horizontal floor. The coefficient of friction between P and the floor is \(\mu\). A force of magnitude 3 N is applied to P upwards at an angle \(\alpha\) above the horizontal, where \(tan \alpha=\frac{3}{4}\). The particle is initially at rest and acceleration at \(2ms^{-2}\).
(a) Find the time it takes for P to travel a distance of 1.44 m from its starting point.
(b) Find \(\mu\).
Answer/Explanation
Ans:
(a) \([1.44 = 0 + 1/2 \times 2r^2]\)
t = 1.2s
(b) \(R = 0.4g – 3 \times \frac{3}{5}=0.4g – 3 sin 36.9 [ =2.2]\)
\([3 \times \frac{4}{5}-F=3 cos 36.9 – F = 0.4 \times 2] [F=1.6]\)
\([\mu=\frac{3 \times \frac{4}{5}=0.4 \times 2}{0.4g – 3 \times \frac{3}{5}}=\frac{1.6}{2.2}]\)
\(\mu=0.727\)
Question
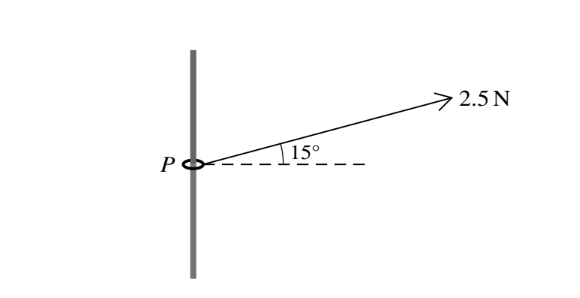
A small ring P of mass 0.03 kg is threaded on a rough vertical rod. A light inextensible string is
attached to the ring and is pulled upwards at an angle of 15Å to the horizontal. The tension in the string is 2.5 N (see diagram). The ring is in limiting equilibrium and on the point of sliding up the
rod. Find the coefficient of friction between the ring and the rod.
Answer/Explanation
R = 2.5 cos 15 [F = μ × 2.5 cos 15]
[2.5 sin 15 = 0.03g +F] μ = 0.144
Question
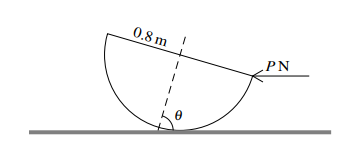
A uniform solid hemisphere of weight 60 N and radius 0.8 m rests in limiting equilibrium with its curved surface on a rough horizontal plane. The axis of symmetry of the hemisphere is inclined at an angle of ∅ to the horizontal, where cos ∅ = 0.28. Equilibrium is maintained by a horizontal force of magnitude P N applied to the lowest point of the circular rim of the hemisphere (see diagram).
(i) Show that P = 8.75. [3]
(ii) Find the coefficient of friction between the hemisphere and the plane. [2]
Answer/Explanation
Ans:

Question
A particle is projected from a point P with initial speed u \(ms^{-1}\) up a line of greatest slope PQR of a rough inclined plane. The distances PQ and QR are both equal to 0.8 m. The particle takes 0.6 s to
travel from P to Q and 1 s to travel from Q to R.
(i) Show that the deceleration of the particle is \(\frac{2}{3} ms^{-1}\)
and hence find u, giving your answer as an exact fraction.
(ii) Given that the plane is inclined at 3Å to the horizontal, find the value of the coefficient of friction
between the particle and the plane.
Answer/Explanation
(i) For PQ 0.8 = 0.6u+ 0.18a
For PR 1.6= 1.6u+ 1.28 a
Deceleration =\( \frac{2}{3}ms^{-2}\)
\(u=\frac{23}{15}\)
Question
A particle of mass 12 kg is on a rough plane inclined at an angle of 25Å to the horizontal. A force of
magnitude P N acts on the particle. This force is horizontal and the particle is on the point of moving up a line of greatest slope of the plane. The coefficient of friction between the particle and the plane is 0.8. Find the value of P.
Answer/Explanation
[R = 12g cos 25 + P sin 25
P cos 25 = F + 12g sin 25]
or
[P = F cos 25 + R sin 25
R cos 25 = F sin 25 + 12g]
F = 0.8R
Complete method to find P from 2
equations(3 terms each)
P = 242
Question
A particle P of mass 0.8 kg is placed on a rough horizontal table. The coefficient of friction between P and the table is μ. A force of magnitude 5 N, acting upwards at an angle α above the horizontal, where tan \(\alpha = \frac{3}{4}\) , is applied to P. The particle is on the point of sliding on the table.
(i) Find the value of μ. [4]
(ii) The magnitude of the force acting on P is increased to 10 N, with the direction of the force remaining the same. Find the acceleration of P. [3]
Answer/Explanation
(i) 5cos α = F [F = 4]
R + 5sin α = 8 [R = 5]
4 = 5µ
µ = 0.8
(ii) R + 10sin α = 8 [R = 2]
and
F = 0.8 × R [F =1.6]
10cos α – F = 0.8a
a = 8ms–2
Question
A particle P of mass 0.6 kg is attached to one end of a light elastic string of natural length 0.8 m and modulus of elasticity 24 N. The other end of the string is attached to a fixed point A, and P hangs in equilibrium.
(i) Calculate the extension of the string. [2]
P is projected vertically downwards from the equilibrium position with speed 4.5 m s−1.
(ii) Find the distance AP when the speed of P is 3.5 m s−1 and P is below the equilibrium position.[4]
(iii) Calculate the speed of P when it is 0.5 m above the equilibrium position. [3]
Answer/Explanation
Ans:

Question
A block of weight 6.1 N slides down a slope inclined at \(tan^{-1}\frac{11}{60}\) to the horizontal. The coefficient of friction between the block and the slope is \(\frac{1}{4}\)). The block passes through a point A with speed 2 m s−1. Find how far the block moves from A before it comes to rest. [5]
Answer/Explanation

Alternative method
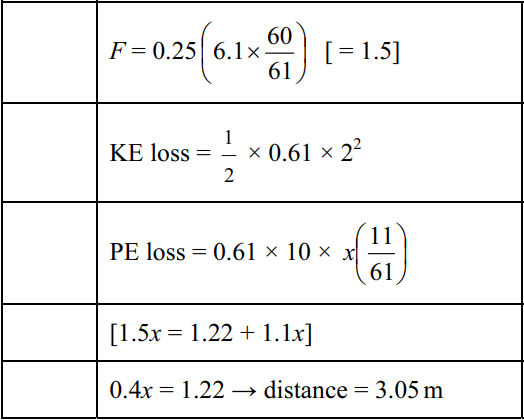
Question
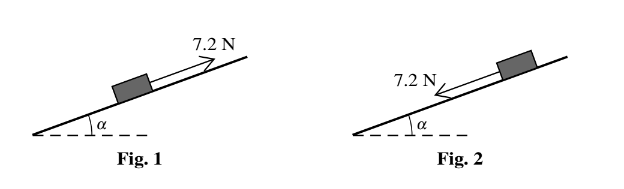
A block of weight 7.5 N is at rest on a plane which is inclined to the horizontal at angle\( \alpha\) , where
\(tan \alpha\) =\( \frac{7}{24}\)The coefficient of friction between the block and the plane is\( \mu\) A force of magnitude
7.2 N acting parallel to a line of greatest slope is applied to the block. When the force acts up the plane (see Fig. 1) the block remains at rest.
(i) Show that\( – ≥ \frac{17}{24}\) When the force acts down the plane (see Fig. 2) the block slides downwards.
(ii) Show that\( \mu <\frac{31}{24} \)
Answer/Explanation
(i) F + Wsinα = 7.2
[μ × 7.5cosα > 7.2 – 7.5sinα]
μ > 17/24
(ii) [7.2 + 7.5 × (7/25) – μ(7.5 × 24/25) > 0] μ < 31/24
Question
A rough plane is inclined at an angle of \(\alpha^{\circ}\) to the horizontal. A particle of mass 0.25 kg is in equilibrium on the plane. The normal reaction force acting on the particle has magnitude 2.4 N. Find
(i) the value of ,
(ii) the least possible value of the coefficient of friction.
Answer/Explanation
(i) 2.4 = 0.25g cosα
α = 16.3
(ii) [μ = 0.28÷0.96]
Least possible value of μ
is 7/24 or 0.292
Question
Particles P and Q are moving in a straight line on a rough horizontal plane. The frictional forces are the only horizontal forces acting on the particles.
(i) Find the deceleration of each of the particles given that the coefficient of friction between P and the plane is 0.2, and between Q and the plane is 0.25. [2]
At a certain instant, P passes through the point A and Q passes through the point B. The distance AB is 5 m. The velocities of P and Q at A and B are 8 m s−1 and 3 m s−1, respectively, both in the direction AB.
(ii) Find the speeds of P and Q immediately before they collide. [5]
Answer/Explanation

Question
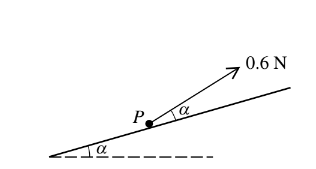
A particle P of mass 0.5 kg rests on a rough plane inclined at angle α to the horizontal, where sin α = 0.28. A force of magnitude 0.6 N, acting upwards on P at angle α from a line of greatest slope of the plane, is just sufficient to prevent P sliding down the plane (see diagram). Find
(i) the normal component of the contact force on P,
(ii) the frictional component of the contact force on P,
(iii) the coefficient of friction between P and the plane.
Answer/Explanation
(i) [R + 0.6sinα = 0.5g cosα ] Normal component is 4.63(2) N
(ii) F + 0.6cosα = 0.5g sinα
Frictional component is 0.824 N
(iii) Coefficient is 0.178
Question
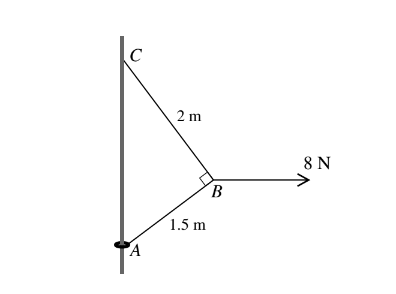
A small ring of mass 0.2 kg is threaded on a fixed vertical rod. The end A of a light inextensible string
is attached to the ring. The other end C of the string is attached to a fixed point of the rod above A. A horizontal force of magnitude 8 N is applied to the point B of the string, where AB = 1.5 m and BC = 2 m. The system is in equilibrium with the string taut and AB at right angles to BC (see diagram).
(i) Find the tension in the part AB of the string and the tension in the part BC of the string. The equilibrium is limiting with the ring on the point of sliding up the rod.
(ii) Find the coefficient of friction between the ring and the rod.
Answer/Explanation
(i)
\(T_{C}\) × (2/2.5) –\( T_{A} \)× (1.5/2.5) = 0
\(T_{C}\) × (1.5/2.5) +\( T_{A}\) × (2/2.5) = 8
[0.6 TC + 0.8\( (4T_{C}/3)\) = 8 → (5/3) TC = 8 or
0.6(0.75TA) + \(0.8T_{A} \)= 8 → \(1.25T_{A}\) = 8 ]
Tension in AB is 6.4 N; tension in BC is 4.8 N
(ii)
F + 0.2 g =\( T_{A}\) × (1.5/2.5) N = TA × (2/2.5)
[ μ = (3.84 – 2 )/5.12]
horizontal Coefficient is 0.359
Question
A cylindrical container is open at the top. The curved surface and the circular base of the container are both made from the same thin uniform material. The container has radius 0.2 m and height 0.9 m.
(i) Show that the centre of mass of the container is 0.405 m from the base. The container is placed with its base on a rough inclined plane. The container is in equilibrium on the point of slipping down the plane and also on the point of toppling.
(ii) Find the coefficient of friction between the container and the plane.
Answer/Explanation
2(i) M = 2π x 0.2 x 0.9 + π x 0.2^{2}
(2π x 0.2 x 0.9 + π x 0.2^{2}) \(\bar{x}\)
= 2π x 0.2 x 0.9 x 0.9/2
\( \bar{x}\) = 0.405 m
2(ii) tanθ = 0.2/0.405
μ = tanθ
μ = 0.494
