Question
Show that \(\int_{1}^{4}x^-\frac{3}{2}\)In \(xdx=2-In4\).
Integrate by parts and reach \(ax^{\tfrac{1}{2}}Inx+b\int x^{\frac{-1}{2}}.\frac{1}{2}dx\) Obtain \(-2x^{\frac{-1}{2}}In x+2\int x^{\frac{-1}{2}}.\frac{1}{x}dx\), or equivalent Complete the integration, obtaining \(-2x^{\frac{1}{2}}Inx-4\)
Answer/Explanation
\(x^{\frac{1}{2}}\),or equivalent Substitute limits correctly, having integrated twice Obtain the given answer following full and correct working
Question
The parametric equations of a curve are
x = e−t cost, y = e−t sin t.
Show that \(\frac{dy}{dx}= tan \left ( t-\frac{1}{4}\pi \right )\) .[6]
Answer/Explanation
Ans:

Question
(a) Show that \(\int_{2}^{4}4xlnxdx=56ln2-12\). [5]
(b) Use the substitution u = sin 4x to find the exact value of \(\int_{0}^{\frac{1}{24}\pi }cos^{3}4xdx.\) [5]
Answer/Explanation
Ans:
(a) Carry out integration by parts and reach \(ax^{2}lnx+b\int \frac{1}{2}x^{2}dx\)
Obtain \(2x^{2}lnx-\int \frac{1}{x}.2x^{2}dx\)
Obtain \(2x^{2}lnx-x^{2}\)
Use limits, having integrated twice
Confirm given result 56 ln 2 – 12
(b) State or imply \(\frac{du}{dx}=4cos4x\)
Carry out complete substitution except limits
Obtain \(\int \left ( \frac{1}{4}- \frac{1}{4}u^{2}\right )du\) or equivalent
Integrate to obtain form k1u + k2u3 with non-zero constants k1, k2
Use appropriate limits to obtain \(\frac{11}{96}\)
Question
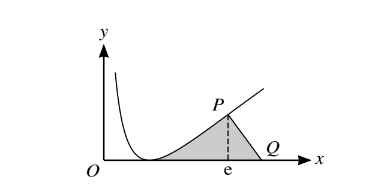
The diagram shows the curve \(y =(Inx)^{2}\)
The x-coordinate of the point P is equal to e, and the normal to the curve at P meets the x-axis at Q.
(i) Find the x-coordinate of Q.
(ii) Show that\( \int In x dx = x ln x − x + c, where c is a constant.
(iii) Using integration by parts, or otherwise, find the exact value of the area of the shaded region
between the curve, the x-axis and the normal PQ.
Answer/Explanation
(1) State or imply derivative is\( 2\frac{Inx}{x}\)
State or imply gradient of the normal at x =\( e is -\frac{1}{2}e,\)or equivalent
Carry out a complete method for finding the x-coordinate of Q
Obtain answer\( x=e+\frac{2}{e}\) exact equivalent
(ii) Justify the given statement by integration or by differentiation
(iii) Integrate by parts and reach \(ax(Inx)^{2}+b\int x.\frac{Inx}{x}dx\) Complete the integration and obtain x(In x)2 – 2x In x + 2x, or equivalent
use limits x = 1 and x = e correctly, having integrated twice
Obtain exact value e-2
Use x-coordinate of Q found in part (i) and obtain final answer\( e-2+\frac{1}{e}\)
Question
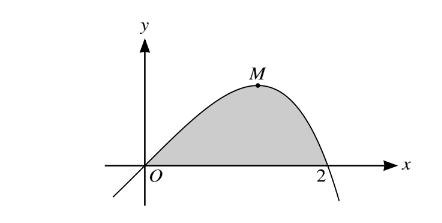
The diagram shows part of the curve\( y =(2x-x^{2})e^{\frac{1}{2}x}\) and its maximum point M.
(i) Find the exact x-coordinate of M.
(ii) Find the exact value of the area of the shaded region bounded by the curve and the positive x-axis
Answer/Explanation
.
(i) Use the correct product rule
Obtain correct derivative in any form, e.g.\( (2-2x)e^{\frac{1}{2}}+\frac{1}{2}(2x-x^{2})e^{\frac{1}{2}x}\)
Equate derivative to zero and solve for x
Obtain\( x \sqrt{5-1}\)
(ii) Integrate by parts and reach \(a(2x x^{2})e^{\frac{1}{2}x}+b\int (2-2x)e^{\frac{1}{2}x}dx\)
Obtain
\(2e^{\frac{1}{2}x}(2x-x^{2})-2\int (2-2x)e^{\frac{1}{2}x}\)
Complete the integration correctly, obtaining\( (12x-2x^{2}-24)e^{\frac{1}{2}}\)
Use limits x = 0, x = 2 correctly having integrated by parts twice
Obtain answer 24 – 8e, or exact simplified equivalent
Question
Find the exact value of \(\int_{0}^{\frac{1}{2}} xe^{-2x}dx\)
Integrate by parts and reach \(axe^{-2x}+b\int e^{-2x}\)
Obtain \(\frac{1}{2}xe^{-2x}+\frac{1}{2},\int e^{-2x}\)dx or equivalent
Complete the integration correctly, obtaining\( -\frac{1}{2}xe^{-2x}\)
Answer/Explanation
\(-\frac{1}{4}e^{-2x}\),or equivalent
Use limits x = 0 and \(x=\frac{1}{2} \)correctly, having integrated twice
Obtain answer\( \frac{1}{4}-\frac{1}{2}e^{-1}\) , or exact equivalent
