Question
The planes m and n have equations 3x + y − 2z = 10 and x − 2y + 2z = 5 respectively. The line l has
equation r = 4i + 2j + k + \lambda (i + j + 2k).
(i) Show that l is parallel to m.
(ii) Calculate the acute angle between the planes m and n.
(iii) A point P lies on the line l. The perpendicular distance of P from the plane n is equal to 2. Find
the position vectors of the two possible positions of P.
Answer/Explanation
(i) EITHER: Expand scalar product of a normal to m and a direction vector of l
Verify scalar product is zero
Verify that one point of l does not lie in the plane
OR: Substitute coordinates of a general point of l in the equation of the plane m
Obtain correct equation in
λ in any form Verify that the equation is not satisfied for any value of λ 3
(ii) Use correct method to evaluate a scalar product of normal vectors to m and n
Using the correct process for the moduli, divide the scalar product by the product of the moduli and evaluate the inverse cosine of the result
Obtain answer 74.5° or 1.30 radians 3
(iii) EITHER: Using the components of a general point
P of l form an equation in
λ by
equating the perpendicular distance from n to 2
OR: Take a point Q on l, e.g. (5, 3, 3) and form an equation in λ by equating the
length of the projection of QP onto a normal to plane n to 2
Obtain a correct modular or non-modular equation in any form Solve for λ and obtain a position vector for P, e.g. 7i + 5j + 7j from λ = 3
Obtain position vector of the second point, e.g. 3i + j – k from λ = – 1
Question
Two lines l and m have equations \(r=ai+2j+3k+\lambda (i-2j+3k) and r=2i+j+2k+\mu (2i-j+k)\) respectively, where a is a constant. It is given that the lines intersect.
(i) Find the value of a.
(ii) When a has this value, find the equation of the plane containing l and m.
Answer/Explanation
(i) Express general point of l or m in component form
e.g. (a +λ, 2 – 2λ, 3 + 3λ) or(2 + 2μ, 1 –μ, 2 +μ)
Equate at least two pairs of corresponding components and solve for λ or for μ
Obtain either λ = – 2 or μ = – 5
or\( \lambda = \frac{1}{3}a or \mu =\frac{2}{3}a-1\)
or\( \lambda =\frac{1}{5}(a-4) or \mu =\frac{1}{5}(3a-7)\) Obtain a = – 6
(ii) Use scalar product to obtain a relevant equation in a, b and c, e.g. a – 2b + 3c = 0
Obtain a second equation, e.g. 2a – b + c = 0 and solve for one ratio
Obtain a : b : c = 1 : 5 : 3
Substitute a relevant point and values of a, b, c in general equation and find d
Obtain correct answer x + 5y + 3z = 13
Alternative method for question (ii)
Attempt to calculate vector product of relevant vectors,
Obtain two correct components
Obtain correct answer, e.g. i + 5j + 3k
Substitute a relevant point and find d
Obtain correct answer x + 5y + 3z = 13
(ii) Alternative method for question (ii)
Using a relevant point and relevant vectors, form a 2-parameter equation for the plane
State a correct equation, e.g. r = 2i + j + 2k +λ(i – 2j + 3k) +μ(2i – j + k)
State three correct equations in x, y, z, λ and μ
Eliminate λ and μ
Obtain correct answer x + 5y + 3z = 13
Question
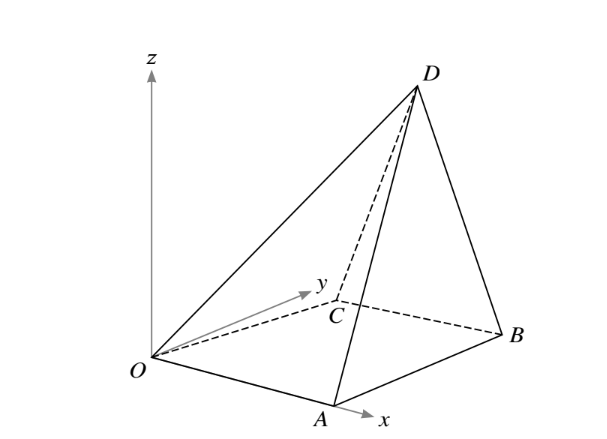
The diagram shows a set of rectangular axes Ox, Oy and Oz, and four points A, B, C and D with position vectors \(\vec{OA}=3i,\vec{OB}=3i+4j,\vec{OC}=i+3j and \vec{OD}=2i+3j+5k.\)
(i) Find the equation of the plane BCD, giving your answer in the form ax + by + cz = d.
(ii) Calculate the acute angle between the planes BCD and OABC.
Answer/Explanation
(i) Obtain a vector parallel to the plane, e.g.\(\overrightarrow{CB}=2i+j\)
Use scalar product to obtain an equation in a,b,c
Obtain two correct equation in a,b,c
Solve to obtain a:b:c,
Obtain a:b:c:-10:-1,
Obtain equation 5x-10y-z=-25
Alternative method 1
Obtain a vector p[arallel to the plane ,eg..\(\overrightarrow{CB}=2i+j\)
Obtain a second such vector and calculate thier vector product ,e.g. \(\left ( 2i+J \right )\times \left ( i+5k \right )\)
Obtain two correct components
Obtain correct answer e.g. 5i-10j-k
Substitute to find d
Obtain equation 5x-10y-z=-25
Alternative method 2
Obtain a vector parallel to the palne e.g,\(\overrightarrow{DB}=i+j-5k\)
Obtain a second vector aqnd form correctly a 2-parameter equation for the plane
State a correct equation in x,y,z,\(\Lambda \) and \(\mu \)
Eliminate \(\Lambda \) and \(\mu \)
Obtain equation 5x-10y-z=-25
Alternative Method 3
Substitute for B and C and obtain 3a+4b=d and a+3b=d
Substitute for D to obtain a third equation and eliminatye one unknown 9a,b<ord) entirely
Obtain two correct equation in two unknowns,e.g.a:b:c
Solve to obtain their ratio ,e.g.a:b:c
Obtain a:b:c=5:-10:-1
a:c:d=5:-1:-25 or b:c:d=10:1:25
Obtain equation 5x-10y-z=-25
Alternate Method 4
Substitute for B and C and obtain 3a+4b=d and a+3b+d
Solve to obtain a:b:d
Obtain a:b:d=1:-2:-5
Substitute for C to obtain c
Obtain equation 5x-10y-z=-25.
(ii) State or imply a normal vector for the plane OABC is k
Carry out correct process for evaluating a scalar product of relevant the inverse consine of the result
Obtain answer\( 84.9^{\circ}\)( or 1.48 radian
Question
Two planes have equations 2x+ 3y − z = 1 and x − 2y + z = 3.
(i) Find the acute angle between the planes.
(ii) Find a vector equation for the line of intersection of the planes.
Answer/Explanation
(i) State or imply a correct normal vector to either plane, e.g. 2i + 3j – k, or i –2j +k
Carry out correct process for evaluating the scalar product of two normal vectors
Using the correct process for the moduli, divide the scalar product of the two normal vectors by the product of their moduli and evaluate the inverse cosine of the result
Obtain answer 56.9° or 0.994 radians
(ii) EITHER: Carry out a complete strategy for finding a point on the line (call the line l)
Obtain such a point, e.g. (1, 1, 4)
EITHER: State a correct equation for a direction vector ai +bj +ck for l,e.g. 2a+ 3b – c = 0
State a second equation, e.g. a – 2b + c = 0, and solve for one ratio, e.g. a: b
Obtain a : b : c = 1 : – 3: – 7, or equivalent
State a correct answer, e.g. r= i + j + 4k +λ(i – 3j –7k)
OR1: Attempt to calculate the vector product of the two normal vectors
Obtain two correct components
Obtain i – 3j – 7k, or equivalent
State a correct answer, e.g. r= i + j + 4k +λ(i – 3j – 7k), or equivalent
OR2: Obtain a second point on l e.g. (0, 4, 11)
Subtract position vectors and obtain a direction vector for l
Obtain i – 3j – 7k, or equivalent
State a correct answer, e.g. r = 4j + 11k +μ(i – 3j – 7k), or equivalent
OR3: Express one variable in terms of a second
Obtain a correct simplified expression, e.g. y x = 4 −3x
Express the third variable in terms of the second
Obtain a correct simplified expression, e.g. z x = 11 − 7x
Form a vector equation for the line
State a correct answer, e.g. r= 4j + 11k +λ(i – 3j – 7k), or equivalent
OR4: Express one variable in terms of a second
Obtain a correct simplified expression, e.g. \(x=\frac{4}{3}-\frac{y}{3}\)
Express the same variable in terms of the third
Obtain a correct simplified expression, e.g. \(x=\frac{11}{7}-\frac{z}{7}\)
Form a vector equation for the line
Obtain a correct answer, e.g.r = 4j + 11k+μ(i – 3j –7k), or equivalent
Question
The equations of two linesl and m are \(r=3i-j-2k+\lambda (-i+j+4k)\) and \(r=4i+4j-3k+\mu (2i+j-2k)\) respectively.
(i) Show that the lines do not intersect.
(ii) Calculate the acute angle between the directions of the lines.
(iii) Find the equation of the plane which passes through the point (3, −2, −1) and which is parallel to both l and m. Give your answer in the form ax + by + cz = d
Answer/Explanation
.

Question
The points P and Q have position vectors, relative to the origin O, given by
\(\underset{OP}{\rightarrow}=7i+7j-5k\) and \(\underset{OQ}{\rightarrow}=5i+j+k.
The mid-point of PQ is the point A. The plane \(\mathbb{I}\) is perpendicular to the line PQ and passes through A.
(i) Find the equation of \(\mathbb{I}\), giving your answer in the form ax + by + cz = d. [4]
(ii) The straight line through P parallel to the x-axis meets \(\mathbb{I}\) at the point B. Find the distance AB, correct to 3 significant figures. [5]
Answer/Explanation
Ans:
(i) State or imply A is (1, 4, –2)
State or imply \(\underset{QP}{\rightarrow}=12i+6j-6k\) or equivalent
Use QP as normal and A as mid-point to find equation of plane
Obtain 12x + 6y – 6z = 48 or equivalent
(ii) Either State equation of PB is r = 7i + 7j – 5k + λi
Set up and solve a relevant equation for λ .
Obtain λ = −9 and hence B is (–2, 7, –5)
Use correct method to find distance between A and B.
Obtain 5.20
Or Obtain 12 for result of scalar product of QP and i or equivalent
Use correct method involving moduli, scalar product and cosine to find angle APB
Obtain 35.26° or equivalent
Use relevant trigonometry to find AB
Obtain 5.20
Question
The plane with equation 2x + 2y − z = 5 is denoted by m. Relative to the origin O, the points A and B have coordinates (3, 4, 0) and (−1, 0, 2) respectively.
(i) Show that the plane m bisects AB at right angles.
A second plane p is parallel to m and nearer to O. The perpendicular distance between the planes is 1.
(ii) Find the equation of p, giving your answer in the form ax + by + cz = d.
Answer/Explanation
6(i) State or obtain coordinates (1, 2, 1) for the mid-point of AB
Verify that the midpoint lies on m
State or imply a correct normal vector to the plane, e.g. 2 i+2 j-k
State or imply a direction vector for the segment AB, e.g. −4i-4j+2k
Confirm that m is perpendicular to AB
6(ii) State or imply that the perpendicular distance of m from the origin is \(\frac{5}{3}\) , or
unsimplified equivalent
State or imply that n has an equation of the form 2x+2y-z=k
Obtain answer 2x+2y-z=2
Question
The line l has equation r = i + 2j − 3k + ,2i − j + k. The plane p has equation 3x + y − 5z = 20.
(i) Show that the line l lies in the plane p.
(ii) A second plane is parallel to l, perpendicular to p and contains the point with position vector
3i − j + 2k. Find the equation of this plane, giving your answer in the form ax + by + cz = d.
Answer/Explanation
(i) Verify that the point with position vector i jk + 2 3 − lies in the plane
EITHER:
Find a second point on l and substitute its coordinates in the equation of p
Verify that the second point, e.g. (3, 1, – 2), lies in the plane
OR:
Expand scalar product of a normal to p and the direction vector of l
Verify scalar product is zero

Obtain answer 4 13 5 9 x yz + += , or equivalent
Question
Two lines have equations \(r=i+2j+k+\lambda (ai+2j-k)\ and \ r=21+j-k+\mu (2i-j+k),\) , where a is a
constant.
(a) Given that the two lines intersect, find the value of a and the position vector of the point of
intersection. [5]
(b) Given instead that the acute angle between the directions of the two lines is \(\cos ^{-1}(\frac{1}{6})\). find the
two possible values of a. [6]
Answer/Explanation
(b) Use correct process for finding the scalar product of direction
Using the correct process for the moduli, divide the scalar
product by the product of the moduli and equate the result to
\(\pm \frac{1}{6}\)
State a correct equation in a in any form, \(e.g.\frac{2a-2-1}{\sqrt{6}\sqrt{(a^{2}+5)}}=\pm \frac{1}{6}\)
Solve for a
Obtain a = 1
Obtain \(a=\frac{49}{23}\)
(b) Alternative method for question(b)
\(\cos (\theta )=[|a^{2}+2^{2}+(-1)^{2}|^{2}+|2^{2}+(-1)^{2}+1^{2}|^{2}-|(a-2)^{2}+3^{2}+(-2)^{2}|^{2}]/[2|a^{2}+2^{2}+(-1)^{2}|.|2^{2}+(-1)^{2}+1^{2}|]\)
Equate the result to \(\pm \frac{1}{6}\)
Solve for a
Obtain a = 1
Obtain \(a=\frac{49}{23}\)
Question
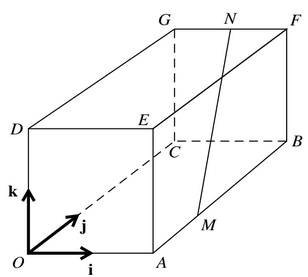
In the diagram, OABCDEFG is a cuboid in which OA=2 units, OC = 3 units and OD = 2 units. Unit vectors i, j and k are parellel to OA, OC and OD respectively. The point M on AB is such that MD = 2AM. The midpoint of FG is N.
(a) Express the vectors \(\overrightarrow{OM}\) and \(\overrightarrow{MN}\) in terms of i, j and k
(b) Find a vector equation for the line through M and N.
(c) Find the position vector of P, the foot of the perpendicular from D to the line through M and N.
Answer/Explanation
Ans:
(a) Obtain \(\overrightarrow{OM}=2i+j\)
Use a correct method to find \(\overrightarrow{MN}\)
Obtain \(\overrightarrow{MN}=-i+2j+2k\)
(b) Use a correct method to form an equation for MN
Obtain \(r=2i+j+ \lamdba(-i+2j+2k)\), or equivalent
(c) Find \(\overrightarrow{DP}\) for a point P on MN with parameter \(\lambda, e.g.(2- \lambda,1+2\lambda,-2+2\lambda)\)
Equate scalar product of \(\overrightarrow{DP}\) and a direction vector for MN to zero and solve for \(\lambda\).
Obtain\(\lambda=\frac{4}{9}\)
State that the position vector of P is \(\frac{14}{9}i+\frac{17}{9}j+\frac{8}{9}k\)
Two lines l and m have equations r = 3i + 2j + 5k + s(4i − j + 3k) and r = i − j − 2k + t(−i + 2j + 2k) respectively.
(a) Question
Show that l and m are perpendicular.
(b) Question
Show that l and m intersect and state the position vector of the point of intersection.
(c) Question
Show that the length of the perpendicular from the origin to the line m is \(\frac{1}{3}\sqrt{5}\) .
Answer/Explanation
Ans:(a)
Use correct method to evaluate the scalar product of relevant vectors
Obtain answer zero and deduce the given statement
Ans:(b)
Express general point of l or m in component form, e.g. (3 + 4s, 2 – s, 5 + 3s) or (1 – t, – 1 +2t, – 2 + 2t)
Equate at least two pairs of components and solve for s or for t
Obtain correct answer s = – 1 and t = 2
Verify that all three equations are satisfied
State position vector of the intersection – i + 3j +2k, or equivalent
Ans:(c)
Taking a general point P on m, form an equation in t by either equating a relevant scalar product to zero, or equating the derivative of \(\left | \overrightarrow{OP} \right |\) to zero, or taking a specific point Q on m, e.g. (1, – 1, – 2), using Pythagoras in triangle OPQ
Obtain t = \(\frac{7}{9}\)
Carry out correct method to find OP
Obtain \(\frac{\sqrt{5}}{3}\)
Question
With respect to the origin O, the points A and B have position vectors given by \(\overrightarrow{OA}=\begin{pmatrix}1\\2\\ 1\end{pmatrix}\ and \ \overrightarrow{OB}=\begin{pmatrix}3\\1\\ -2\end{pmatrix}\). The line l has equation \(r=\begin{pmatrix}2\\3\\1\end{pmatrix}+\lambda \begin{pmatrix}1\\-2\\ 1\end{pmatrix}\).
(a) Find the acute angle between the directions of AB and l. [4]
(b) Find the position vector of the point P on l such that AP = BP. [5]
Answer/Explanation
Ans
(a) State or imply \(\overrightarrow{AB}=\begin{pmatrix}2\\-1 \\ -3\end{pmatrix}\)
Use the correct process to calculate the scalar product of a pair of relevant vectors, e.g. their
\(\overrightarrow{AB}\) and a direction vector for l
Using the correct process for the moduli, divide the scalar product by the
product of the moduli of the two vectors and evaluate the inverse cosine of
the result
Obtain answer 83.7° or 1.46 radians
(b) State or imply \(\pm \overrightarrow{AP}\ and \ \pm \overrightarrow{BP}\) in component form, i.e.
(1 +λ, 1 – 2λ, λ) and (– 1 +λ, 2 – 2λ, 3 +λ), or equivalent
Form an equation in λ by equating moduli or by using cos BAP = cos ABP
Obtain a correct equation in any form
(1+ λ)2+ (1- 2λ)2 + λ2=(λ – 1)2 + (2 – 2λ)2 + (λ + 3)2
Solve for λ and obtain position vector
Obtain correct position vector for P in any form, e.g. (8, – 9, 7) or 8i –9j + 7k
Question
Two lines have equations 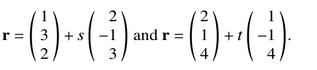
(a) Show that the lines are skew.
(b) Find the acute angle between the directions of the two lines.
Answer/Explanation
Ans:
- Express general point of a line in component for, e.g.
(1+2s,3-s,2+3x) or (2+t,1-t,4+4t)
Equate at least two pairs of components and solve for s of for t
Obtain correct answer for s or for t (possible answers are -1, 6, \(\frac{2}{5}\) for s and -3, 4, -\(\frac{1}{5}\) for t)
Verify that all three component equations are not satisfied
Show that the lines are not parallel and are thus skew - Carry out correct process for evaluating the scalar product of the direction vectors
Using the correct process for the moduli, divide the scalar product by the product of the moduli and evaluate the inverse cosine of the result
Obtain answer \(19.1^o\) or 0.333 radians
Question
Two planes have equations 3x + y − z = 2 and x − y + 2z = 3.
(i) Show that the planes are perpendicular.
(ii) Find a vector equation for the line of intersection of the two planes.
Answer/Explanation
(i)State or imply a correct normal vector to either plane, e.g. 3i jk + − or ij k − + 2
Use correct method to calculate their scalar product
Show value is zero and planes are perpendicular
(ii)
EITHER: Carry out a complete strategy for finding a point on l the line of intersection
Obtain such a point, e.g. (0, 7, 5) , (1, 0, 1), (5/4, –7/4, 0)
EITHER: State two equations for a direction vector ai+bj+ck for l,
e.g. 3a+b-c=0 and a-b+2c=0
Solve for one ratio, e.g. a : b
Obtain a : b : c = 1 : −7 : −4, or equivalent
State a correct answer, e.g. r=7j+5k+Λ(i-7j+4k)
OR1: Obtain a second point on l, e.g. (1, 0, 1)
Subtract vectors and obtain a direction vector for l
Obtain −i+7j+4k, or equivalent
State a correct answer, e.g. r=i+k+Λ(-i+7j+4k)
OR2: Attempt to find the vector product of the two normal vectors
Obtain two correct components of the product
Obtain i-7j-4k , or equivalent
State a correct answer, e.g. r=i+k+Λ(-i+7j+4k)
OR1: Express one variable in terms of a second variable
Obtain a correct simplified expression, e.g. y = 7 – 7x
Express the third variable in terms of the second
Obtain a correct simplified expression, e.g. z = 5 – 4x
Form a vector equation for the line
Obtain a correct equation, e.g. r=7j+5k+Λ(i-7j-4k)
OR2: Express one variable in terms of a second variable
Obtain a correct simplified expression, e.g. z=5-4x
Express the same variable in terms of the third
Obtain a correct simplified expression e.g. z(7+4y)/7
Form a vector equation for the line
Obtain a correct equation, e.g. \(r=\frac{5}{4}i-\frac{7}{4}j+\Lambda (-\frac{1}{4}i+\frac{7}{4}j+k)\)
Question
The points A and B have position vectors 2i + j + k and i − 2j + 2k respectively. The line l has vector equation r = i + 2j − 3k + μ(i – 3j – 2k).
(a)Find a vector equation for the line through A and B.
(b) Find the acute angle between the directions of AB and l, giving your answer in degrees.
(c) Show that the line through A and B does not intersect the line l.
Answer/Explanation
Ans:
(a)Obtain direction vector −i− 3j+k
Use a correct method to form a vector equation
Obtain answer r = 2i + j + k + λ (-i-3j+k)
or r = i 2j + 2k + λ (-i-3j+k)
(b) Carry out the correct process for evaluating the scalar product of the direction vectors.
Using the correct process for the moduli, divide the scalar product by the product of the moduli and find the inverse cosine of the result for any 2 vectors
Obtain answer 61.1 °
(c)
Express general point of AB or l in component form, e.g. (2 –λ, 1 – 3λ, 1 + λ) or (1 + µ, 2 – 3 µ, – 3 – 2µ)
Equate at least two pairs of components and solve for λ or for µ
Obtain a correct answer for λ or µ, e.g. λ = \(= 6, \frac{1}{6}, or -\frac{14}{9}; \mu = -5, \frac{2}{3} or – \frac{11}{9}\)
Verify that all three equations are not satisfied, and the lines do not intersect
Express general point of AB or l in component form,
e.g. (1 –λ*,− 2 – 3λ*, 2 +λ*) or (1 + µ*, 2 – 3µ*, – 3 – 2µ*)
Question
The line l has equation r = \(\begin{pmatrix}1\\2\\-1\\\end{pmatrix}+\lambda \begin{pmatrix}2\\1\\3\\\end{pmatrix}\) . The plane p has equation r. \(\begin{pmatrix}2\\-1\\-1\\\end{pmatrix}\) = 6.
(i) Show that l is parallel to p. [3]
(ii) A line m lies in the plane p and is perpendicular to l. The line m passes through the point with coordinates (5, 3, 1). Find a vector equation for m. [6]
Answer/Explanation
Ans:
(i) EITHER: Substitute for r in the given equation of p and expand scalar product
Obtain equation in λ in any correct form
Verify this is not satisfied for any value of λ
OR1: Substitute coordinates of a general point of l in the Cartesian equation of plane p
Obtain equation in λ in any correct form
Verify this is not satisfied for any value of λ
OR2: Expand scalar product of the normal to p and the direction vector of l
Verify scalar product is zero
Verify that one point of l does not lie in the plane
OR3: Use correct method to find the perpendicular distance of a general point of l from p
Obtain a correct unsimplified expression in terms of λ
Show that the perpendicular distance is 5/ √6 , or equivalent, for all λ
OR4: Use correct method to find the perpendicular distance of a particular point of l from p
Show that the perpendicular distance is 5/ √6 , or equivalent
Show that the perpendicular distance of a second point is also 5/ √6 , or equivalent
(ii) EITHER: Calling the unknown direction vector ai + bj + ck state equation 2a + b + 3c = 0
State equation 2a – b – c = 0
Solve for one ratio, e.g. a : b
Obtain ratio a : b : c = 1 : 4 : − 2, or equivalent
OR: Attempt to calculate the vector product of the direction vector of l and the normal vector of the plane p, e.g. (2i + j + 3k ) x (2i – j – k)
Obtain two correct components of the product
Obtain answer 2i + 8j – 4k , or equivalent
Form line equation with relevant vectors
Obtain answer r = 5i + 3j + k + µ (i + 4j – 2k), or equivalent
Question
With respect to the origin O, the points A, B and C have position vectors given by
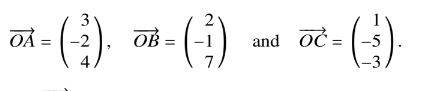
The plane m is parallel to \(\vec{OC}\) and contains A and B.
(i) Find the equation of m, giving your answer in the form ax + by + cß = d.
(ii) Find the length of the perpendicular from C to the line through A and B.
Answer/Explanation
(i) EITHER Use scalar product of relevant vectors, or subtract point equations to form two
equations in a,b,c, e.g. a – 5b – 3c = 0 and a – b – 3c = 0
State two correct equations in a,b,c
Solve simultaneous equations and find one ratio, e.g. a : c, or b = 0
Obtain a : b : c = 3 : 0 : 1, or equivalent
Substitute a relevant point in 3x + z = d and evaluate d
Obtain equation 3x + z = 13, or equivalent
OR 1 Attempt to calculate vector product of relevant vectors,
e.g. (i – 5j – 3k) × (i – j – 3k)
Obtain 2 correct components of the product
Obtain correct product, e.g. 12i + 4k
Substitute a relevant point in 12x + 4z = d and evaluate d
Obtain 3x + z =13, or equivalent
OR 2 Attempt to form 2–parameter equation for the plane with relevant vectors
State a correct equation e.g. r = 3i – 2j + 4k + λ(i – 5j – 3k) + μ(i – j –3k)
State 3 equations in x, y, z, λ and μ
Eliminate λ and μ
Obtain equation 3x + z =13, or equivalent
