Question
(a) Define density.
…………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
(b) Fig. 1.1 shows a solid pyramid with a square base.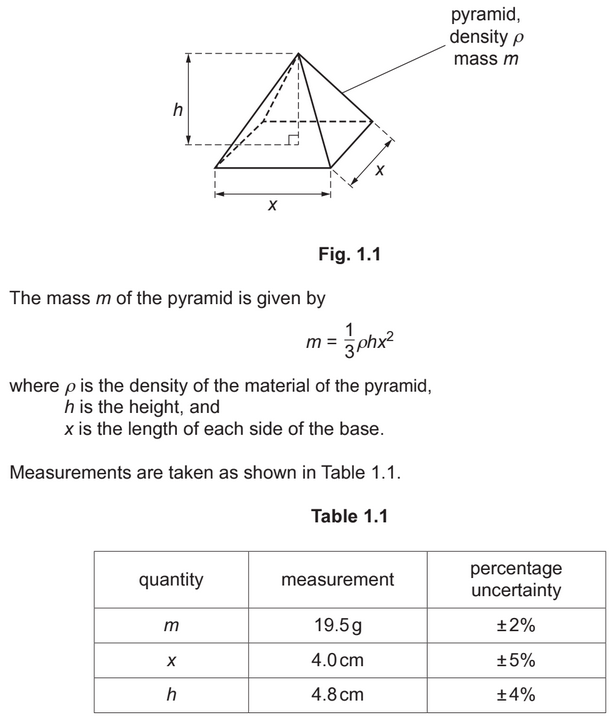
(i) Calculate the absolute uncertainty in length x.
(ii) The density ρ is calculated from the measurements in Table 1.1.
Determine the percentage uncertainty in the calculated value of ρ.
percentage uncertainty = …………………………………………….. %
(c) The square base of the pyramid in (b) rests on the horizontal surface of a bench.
Use data from Table 1.1 to calculate the average pressure of the pyramid on the surface of
the bench. The uncertainty in your answer is not required.
Answer/Explanation
Ans:
(a) mass / volume
(b)(i) absolute uncertainty = 4.0 × (5 / 100)
= (±) 0.2 cm
(b)(ii) percentage uncertainty = 2 + 4 + (5× 2)
= (±) 16%
Question
(a) Define density. [1]
(b) A smooth pebble, made from uniform rock, has the shape of an elongated sphere as shown
in Fig. 1.1.
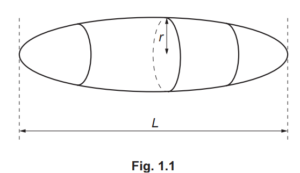
The length of the pebble is L. The cross-section of the pebble, in the plane perpendicular to L,
is circular with a maximum radius r.
A student investigating the density of the rock makes measurements to determine the values
of L, r and the mass M of the pebble as follows:
L = (0.1242 ± 0.0001)m
r = (0.0420 ± 0.0004)m
M = (1.072 ± 0.001)kg.
(i) State the name of a measuring instrument suitable for making this measurement of L. [1]
(ii) Determine the percentage uncertainty in the measurement of r.
percentage uncertainty = …………………………………………….. % [1]
(c) The density ρ of the rock from which the pebble in (b) is composed is given by
where n is an integer and k is a constant, with no units, that is equal to 2.094.
(i) Use SI base units to show that n is equal to –2. [2]
(ii) Calculate the percentage uncertainty in ρ.
percentage uncertainty = …………………………………………….. % [3]
(iii) Determine ρ with its absolute uncertainty. Give your values to the appropriate number of
significant figures.
ρ = ( ……………………………….. ± ……………….) \(kgm^{–3}\) [3]
[Total: 11]
Answer/Explanation
Ans
(a) mass / volume
(b) (i) (vernier/digital) calipers
(b) (ii) percentage uncertainty = (0.0004 / 0.0420) × 100
= 1%
(c) (i) kg m–3 = kg × mn / m or kg m–3 = kg × mn × m–1
–3 =n – 1 and (so) n = –2
(c) (ii) (Δρ /ρ) = (ΔM / M) + 2(Δr / r) + (ΔL / L)
percentage uncertainty = [(0.001 / 1.072) + 2 × (0.0004 / 0.0420) + (0.0001 / 0.1242)] ( × 100)
= 0.09% + 2 × 0.95% + 0.08%
= 2%
(c) (iii) ρ = (1.072 × 0.0420–2) / (2.094 × 0.1242)
= 2337 (kg m–3)
∆ρ = 0.021 × 2337
= 49 (kgm–3)
ρ = (2340 ± 50) kgm–3
