Question
(a) The point P in Fig. 1.1 represents a point mass.
On Fig. 1.1, draw lines to represent the gravitational field around P.

Fig. 1.1
(b) A moon is in circular orbit around a planet.
Explain why the path of the moon is circular.
(c) Many moons are in circular orbit about a planet.
The angular velocity of a moon is ω when the orbit of the moon has a radius r about the planet.
Fig. 1.2 shows the variation of \(r^{3}\) with \(1/ω^{2}\) for these moons.
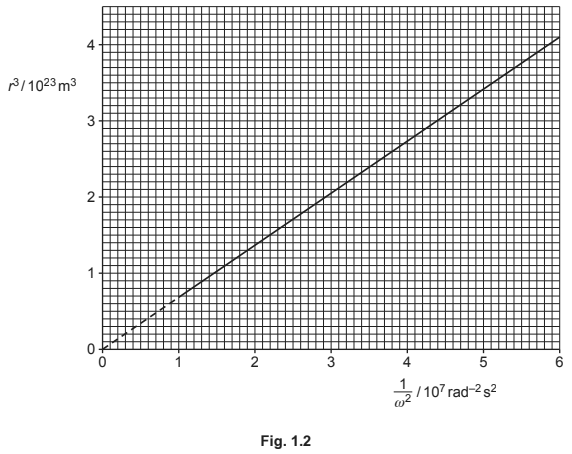
(i) Show that the mass M of the planet is given by the expression
\(M = \frac{gradient}{G}\)
where G is the gravitational constant.
(ii) Use Fig. 1.2 and the expression in (c)(i) to show that the mass M of the planet is \(1.0 \times 10^{26}\) kg.
(iii) Determine the speed of a moon in orbit around the planet with an orbital radius of \(1.2 \times 10^{8}\)m.
Answer/Explanation
Ans:
(a) at least \(4\) straight radial lines to P

all arrows pointing along the lines towards P
(b) Any 2 from:
gravitational force provides the centripetal force
(centripetal or gravitational) force has constant magnitude
(centripetal or gravitational) force is perpendicular to velocity (of moon) / direction of motion (of moon)
(c) (i) \(\frac{GMm}{r^{2}}\) = \(mr\omega ^{2}\)
\(M\) = \(\frac{r^{3}\omega ^{2}}{G}\) and gradient = \(r^{2}\omega ^{2}\) hence M = \(\frac{gradient}{G}\)
or
\(r^{3}\) = \(GM \times 1/\omega ^{2}\) so gradient = GM hence M = \(\frac{gradient}{G}\)
(ii) \(M = 4.1\times 10^{23}/(6.0 \times 10^{7}\times 6.67\times 10^{-11})\) = \(1.0 \times 10^{26}\) kg
(iii) \(\frac{GMm}{r^{2}}\) = \(\frac{mv^{2}}{r}\)
\(\frac{GM}{r}\) = \(v^{2}\)
\(v^{2}\) = \(\frac{6.67\times 10^{-11}\times 1.0\times 10^{26}}{1.2\times 10^{8}}\)
\(v^{2}\) = \(5.6 \times 10^{7}\, ms^{-1}\)
Question
(a) With reference to velocity and acceleration, describe uniform circular motion. [2]
(b) Two cars are moving around a horizontal circular track. One car follows path X and the other follows path Y, as shown in Fig. 1.1.
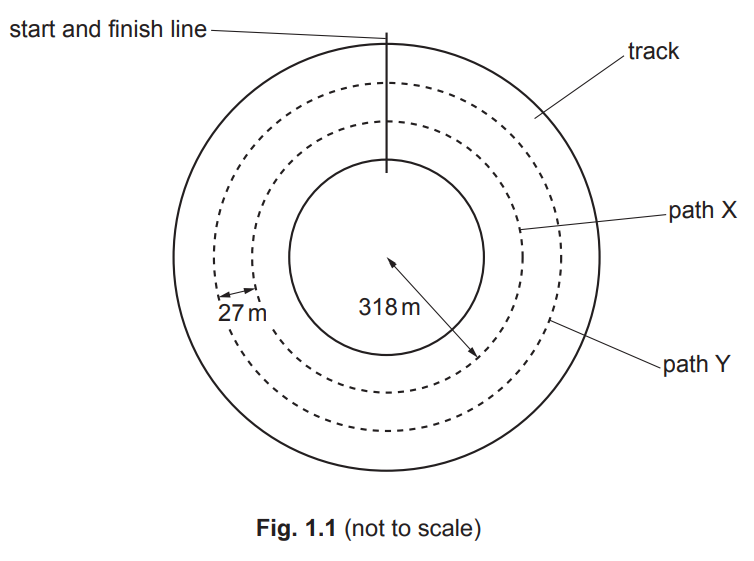
The radius of path X is 318m. Path Y is parallel to, and 27m outside, path X. Both cars have mass 790kg. The maximum lateral (sideways) friction force F that the cars can experience without sliding is the same for both cars.
(i) The maximum speed at which the car on path X can move around the track without sliding is 94ms–1.
Calculate F
(ii) Both cars move around the track. Each car has the maximum speed at which it can move without sliding.
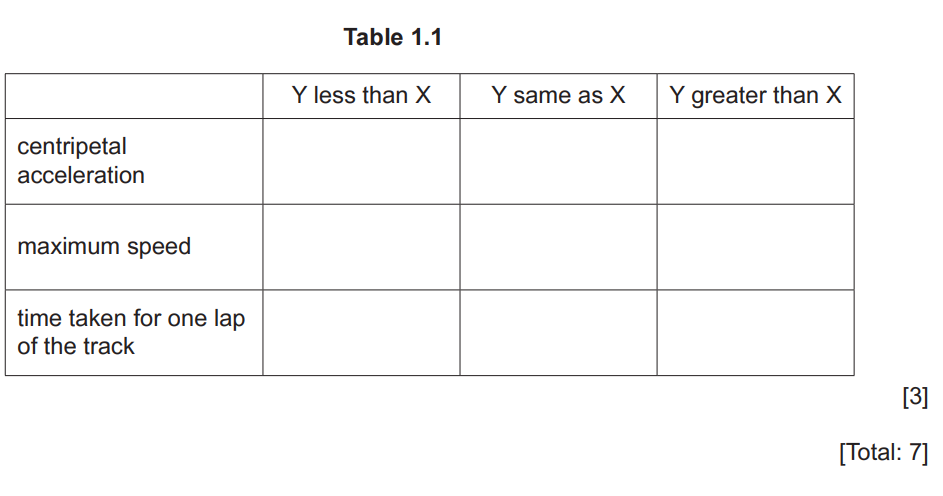
Complete Table 1.1, by placing one tick in each row, to indicate how the quantities indicated for the car on path Y compare with the car on path X
Answer/Explanation
Ans
(a) constant speed or constant magnitude of velocity
acceleration (always) perpendicular to velocity
(b) (i) \(F = mv^2 / r\)
or
v = rω and F = mrω2
F = 790 × 942 / 318
= 22000 N
(b) (ii) centripetal acceleration: same
maximum speed: greater
