Question
A small wooden block (cuboid) of mass m floats in water, as shown in Fig. 3.1.
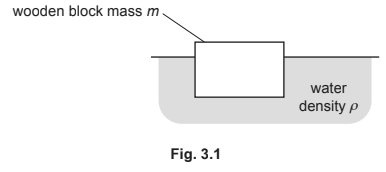
The top face of the block is horizontal and has area A. The density of the water is ρ.
(a) State the names of the two forces acting on the block when it is stationary.
(b) The block is now displaced downwards as shown in Fig. 3.2 so that the surface of the water is higher up the block.

State and explain the direction of the resultant force acting on the wooden block in this position.
(c) The block in (b) is now released so that it oscillates vertically.
The resultant force F acting on the block is given by
F = –Agρx
where g is the gravitational field strength and x is the vertical displacement of the block from the equilibrium position.
(i) Explain why the oscillations of the block are simple harmonic.
(ii) Show that the angular frequency ω of the oscillations is given by
\(\omega = \sqrt{\frac{A\rho g}{m}}\).
(d) The block is now placed in a liquid with a greater density. The block is displaced and released so that it oscillates vertically. The variation with displacement x of the acceleration a of the block
is measured for the first half oscillation, as shown in Fig. 3.3.
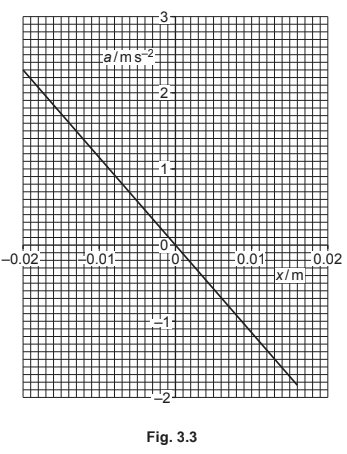
(i) Explain why the maximum negative displacement of the block is not equal to its maximum positive displacement.
(ii) The mass of the block is \(0.57\)kg.
Use Fig. 3.3 to determine the decrease ΔE in energy of the oscillation for the first half oscillation.
Answer/Explanation
Ans:
(a) upthrust, weight
(b) upthrust greater than weight so (resultant force is) upwards
(c) (i) A, g and ρ all constant so F ∝ x
minus sign means F and x are in opposite directions
(ii) \((a = \frac{F}{m}so)\) a = (-)\(\frac{Ag\rho x}{m}\)
so \(\omega ^{2} = \frac{Ag\rho }{m} hence \omega = \sqrt{\frac{Ag\rho }{m}}\)
(d) (i) damping due to viscous forces
(ii) \((E =) 1/2 m\omega ^{2}x_{0}^{2}\)
\(\omega ^{2}\) = (-) gradient
\((E =) 1/2 m\omega ^{2}(x_{1}^{2} – x_{2}^{2})\)
= \(1/2 \times 0.57 \times (2.3/0.020)(0.020^{2} – 0.016^{2})\)
Question
(a) State what is meant by simple harmonic motion.
…………………………………………………………………………………………………………………………………
(b) A trolley of mass m is held on a horizontal surface by means of two springs. One spring is attached to a fixed point P. The other spring is connected to an oscillator, as shown in Fig. 3.1.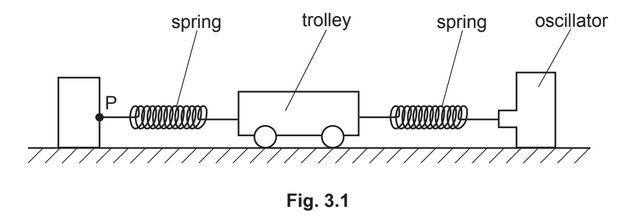
The springs, each having spring constant k of 130Nm−1, are always extended. The oscillator is switched off. The trolley is displaced along the line of the springs and then released. The resulting oscillations of the trolley are simple harmonic. The acceleration a of the trolley is given by the expression
f = ……………………………………………. Hz
(c) The oscillator in (b) is switched on. The frequency of oscillation of the oscillator is varied, keeping its amplitude of oscillation constant. The amplitude of oscillation of the trolley is seen to vary. The amplitude is a maximum at the frequency calculated in (b).
(i) State the name of the effect giving rise to this maximum.
…………………………………………………………………………………………………………………….
(ii) At any given frequency, the amplitude of oscillation of the trolley is constant. Explain how this indicates that there are resistive forces opposing the motion of the trolley.
………………………………………………………………………………………………………………………….
Answer/Explanation
Ans:
(a) acceleration (directly) proportional to displacement
acceleration is in opposite direction to displacement
(b)\(ω^2 = 2k / m \)and \(ω = 2πf\)
\((2πf)^2 = (2× 130) / 0.84 \)
\(f = 2.8 Hz\)
(c)(i) resonance
(c)(ii) oscillator supplies energy (continuously)
energy of trolley constant so energy must be dissipated
or
