Question
A small wooden block (cuboid) of mass m floats in water, as shown in Fig. 3.1.
The top face of the block is horizontal and has area A. The density of the water is ρ.
(a) State the names of the two forces acting on the block when it is stationary.
(b) The block is now displaced downwards as shown in Fig. 3.2 so that the surface of the water is higher up the block.

State and explain the direction of the resultant force acting on the wooden block in this position.
(c) The block in (b) is now released so that it oscillates vertically.
The resultant force F acting on the block is given by
F = –Agρx
where g is the gravitational field strength and x is the vertical displacement of the block from the equilibrium position.
(i) Explain why the oscillations of the block are simple harmonic.
(ii) Show that the angular frequency ω of the oscillations is given by
\(\omega = \sqrt{\frac{A\rho g}{m}}\).
(d) The block is now placed in a liquid with a greater density. The block is displaced and released so that it oscillates vertically. The variation with displacement x of the acceleration a of the block
is measured for the first half oscillation, as shown in Fig. 3.3.
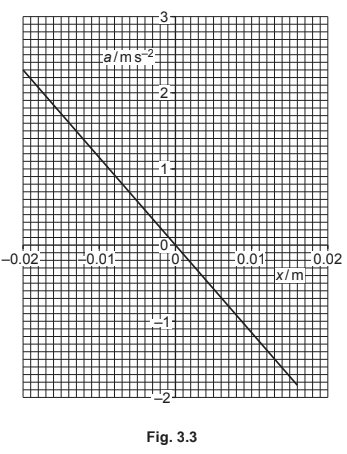
(i) Explain why the maximum negative displacement of the block is not equal to its maximum positive displacement.
(ii) The mass of the block is \(0.57\)kg.
Use Fig. 3.3 to determine the decrease ΔE in energy of the oscillation for the first half oscillation.
Answer/Explanation
Ans:
(a) upthrust, weight
(b) upthrust greater than weight so (resultant force is) upwards
(c) (i) A, g and ρ all constant so F ∝ x
minus sign means F and x are in opposite directions
(ii) \((a = \frac{F}{m}so)\) a = (-)\(\frac{Ag\rho x}{m}\)
so \(\omega ^{2} = \frac{Ag\rho }{m} hence \omega = \sqrt{\frac{Ag\rho }{m}}\)
(d) (i) damping due to viscous forces
(ii) \((E =) 1/2 m\omega ^{2}x_{0}^{2}\)
\(\omega ^{2}\) = (-) gradient
\((E =) 1/2 m\omega ^{2}(x_{1}^{2} – x_{2}^{2})\)
= \(1/2 \times 0.57 \times (2.3/0.020)(0.020^{2} – 0.016^{2})\)
Question
A trolley on a track is attached by springs to fixed blocks X and Y, as shown in Fig. 4.1. The track contains many small holes through which air is blown vertically upwards. This results in the trolley resting on a cushion of air rather than being in direct contact with the track.
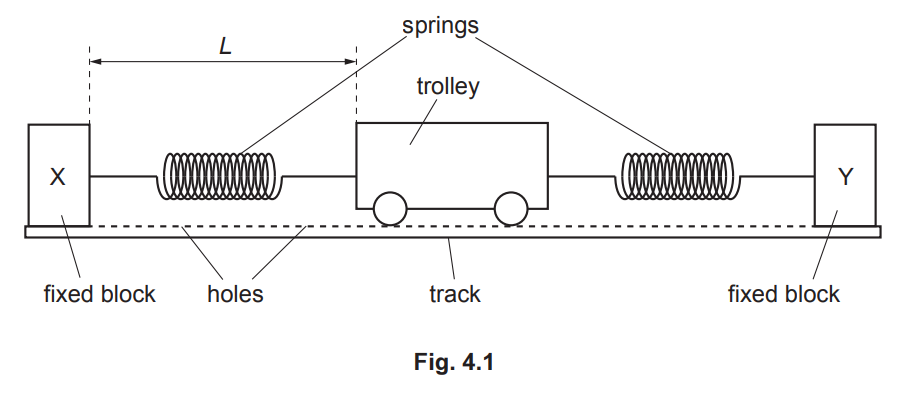
The trolley is pulled to one side of its equilibrium position and then released so that it oscillates initially with simple harmonic motion. After a short time, the air blower is switched off. The variation with time t of the distance L of the trolley from block X is shown in Fig. 4.2.
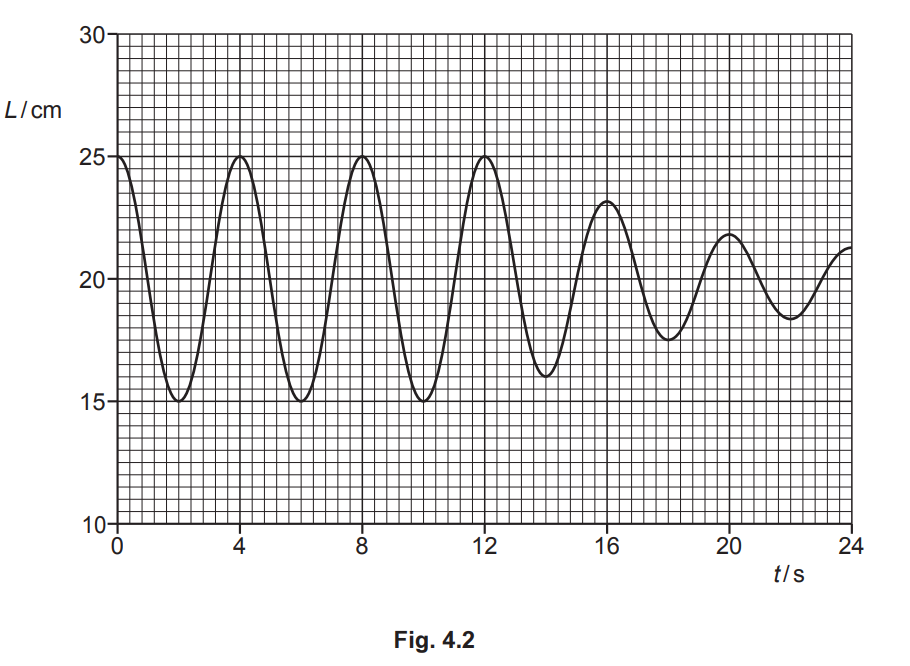
(a) Use Fig. 4.2 to determine:
(i) the initial amplitude of the oscillations
amplitude = …………………………………………… cm [1]
(ii) the angular frequency ω of the oscillations
ω = ………………………………………. rads–1 [2]
(iii) the maximum speed v0, in cms–1, of the oscillating trolley.
\(v_0\) = ………………………………………. cms–1 [2]
(b) Apart from the quantities in (a), describe what may be deduced from Fig. 4.2 about the motion of the trolley between time t = 0 and time t = 24s. No calculations are required. [3]
(c) On Fig. 4.3, sketch the variation with L of the velocity v of the trolley for its first complete
 oscillation.
oscillation.
Answer/Explanation
Ans
(a )(i) 5.0 cm
(a) (ii)ω = 2π / T
or
ω = 2πf and f = 1 / T
ω = 2π / 4.0
= 1.6 rad s–1
(a) (iii) v0 = ωx0
= 1.57 × 5.0
= 7.9 cm s–1
(b) • initial pull was to the right
• distance from X to trolley (at equilibrium) is 20 cm
• period is 4.0 s
• initial motion undamped
• motion becomes damped at/from 12 s
• damping is light
• maximum speed at 1s, 3s, etc. / stationary at 2s, 4s, etc.
Any three points, 1 mark each
(c) sketch: closed loop encircling (20, 0) B1
minimum L shown as 15 cm and maximum L shown as 25 cm
minimum v shown as –7.9 cm s–1 and maximum v shown as +7.9 cms
