Question
(a) Define the tesla.
(b) A magnet produces a uniform magnetic field of flux density B in the space between its poles.
A rigid copper wire carrying a current is balanced on a pivot. Part PQLM of the wire is between
the poles of the magnet, as illustrated in Fig. 8.1.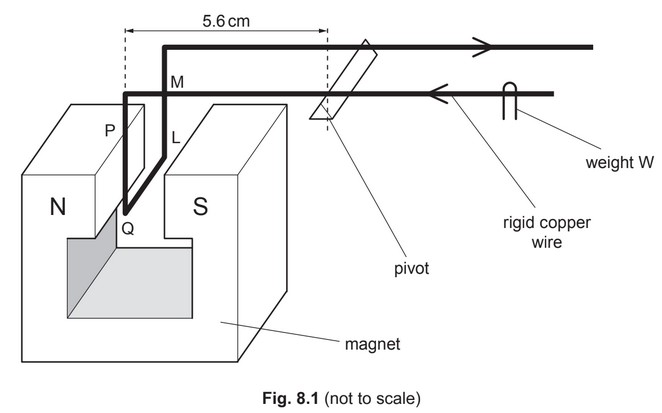
The wire is balanced horizontally by means of a small weight W.
The section of the wire between the poles of the magnet is shown in Fig. 8.2.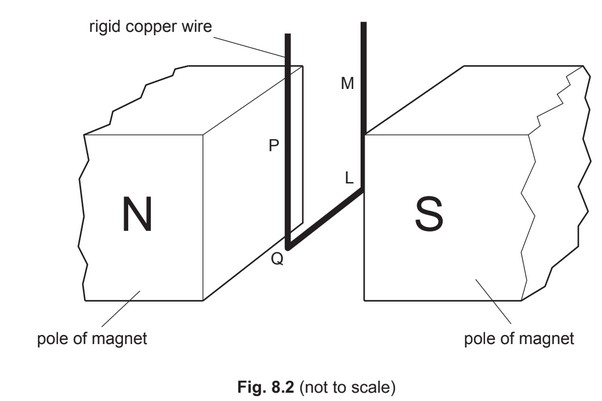
Explain why:
(i) section QL of the wire gives rise to a moment about the pivot
(ii) sections PQ and LM of the wire do not affect the equilibrium of the wire.
(c) Section QL of the wire has length 0.85cm.
The perpendicular distance of QL from the pivot is 5.6cm.
When the current in the wire is changed by 1.2 A, W is moved a distance of 2.6cm along the
wire in order to restore equilibrium. The mass of W is \(1.3 × 10^{–4}\) kg.
(i) Show that the change in moment of W about the pivot is \(3.3 × 10^{–5}\)Nm.
(ii) Use the information in (i) to determine the magnetic flux density B between the poles of the magnet.
B = ……………………………………………… T
Answer/Explanation
Answer:
(a) magnetic field normal to current
newton per ampere
newton per metre
(b) (i) current in wire QL gives rise to a force
or
wire QL is perpendicular to the magnetic field
force on wire QL is vertical
force does not act through the pivot
(ii) forces act through the same line
or
forces are horizontal
forces are equal (in magnitude) and opposite (in direction)
(c) (i) change = mg × (Δ)L
\(= 1.3 × 10^{–4} × 9.81 × 2.6 × 10^{–2} = 3.3 × 10^{–5} N m^{–1}\)
(ii) change =
B × (Δ)I × L × x
\(3.3 × 10^{–5} = B × 1.2 × 0.85 × 10^{–2} × 5.6 × 10^{–2}\)
Question
(a) Explain what is meant by a magnetic field.
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………..
(b) The apparatus shown in Fig. 8.1 is used in an experiment to find the magnetic flux density B between the poles of a horseshoe magnet. Assume the magnetic field is uniform between the poles of the magnet and zero elsewhere.
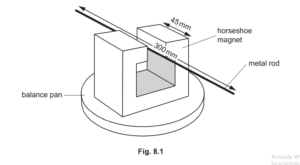
The rigid metal rod of length 300mm is fixed in position perpendicular to the direction of the magnetic field. The poles of the magnet are both 45mm long. There is a current in the rod that causes a force on the rod. The balance is used to determine the magnitude of the force.
The variation with current I of the force F on the rod is shown in Fig. 8.2.
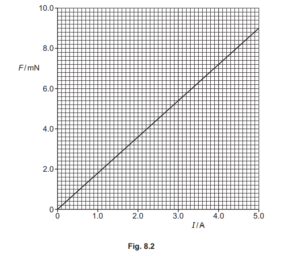
Calculate the magnetic flux density B.
B = ……………………………………………… T
(c) In a different experiment, electrons are accelerated through a potential difference and then enter a region of magnetic field. The magnetic field is into the plane of the paper and is perpendicular to the direction of travel of the electrons, as illustrated in Fig. 8.3.
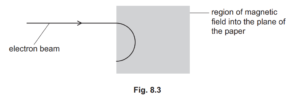
(i) Explain why the electrons follow a circular path when inside the region of the magnetic
field.
………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………….
…………………………………………………………………………………………………………………………
(ii) State the measurements needed in order to determine the charge to mass ratio, e/me, of an electron.
………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………….
…………………………………………………………………………………………………………………………
Answer/Explanation
(a)
a region where a magnet / magnetic material / moving charge / current carrying conductor experiences a force
(b)
B = F / I L
e.g. = 9 × 10–3 / (5.0 × 0.045)
= 0.040 T
(c)(i)
force is (always) perpendicular to the velocity / direction of motion
magnetic force provides the centripetal force
or force perpendicular to motion causes circular motion
magnitude of force (due to the magnetic field) is constant
or
no work done by force
or
the force does not change the speed
(c)(ii)
Applying the list rule, any 2 from:
accelerating p.d.
radius of path / radius of semicircle
