Question
(a) State an experimental phenomenon that provides evidence for:
(i) the particulate nature of electromagnetic radiation
……………………………………………………………………………………………………………………. [1]
(ii) the wave nature of matter.
……………………………………………………………………………………………………………………. [1]
(b) A particle of matter moves with momentum p.
(i) State the equation that gives the effective wavelength λ of the particle. State the name of any other symbols used. [2]
(ii) State the name given to the wavelength of the moving particle.
……………………………………………………………………………………………………………………. [1]
(c) Electrons are accelerated from rest through a potential difference (p.d.) of 4.8kV.
(i) Show that the final speed of the electrons is 4.1 × 107ms–1. [2]
(ii) Calculate the effective wavelength of a beam of electrons moving at the speed in (c)(i).
wavelength = …………………………………………….. m [2] [Total: 9]
Answer/Explanation
Ans
(a) (i) photoelectric effect
(a) (ii) electron diffraction
(b) (i) λ = h / p
h is the Planck constant
(b) (ii) de Broglie (wavelength)
(c )(i) ½mv2 = eV
½ × 9.11 × 10–31 × v2 = 1.60 × 10–19 × 4800 so v = 4.1 × 107 m s–1
(c) (ii) λ = h / mv = 6.63 × 10–34 / (9.11 × 10–31 × 4.1 × 107)
= 1.8 × 10–11
Question
(a) An isolated metal sphere of radius r is charged so that the electric field strength at its surface is E0. On Fig. 6.1, sketch the variation of the electric field strength E with distance x from the centre of the sphere. Your sketch should extend from x = 0 to x = 3r.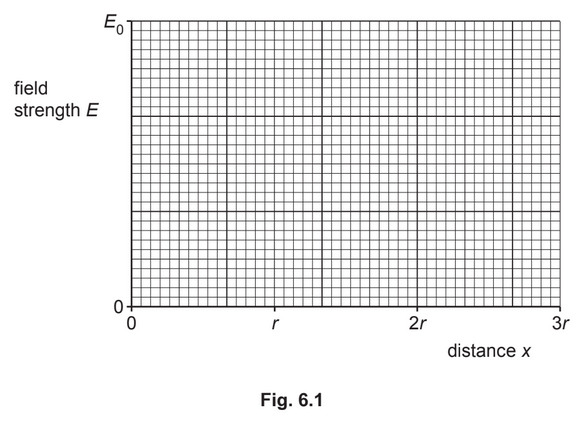
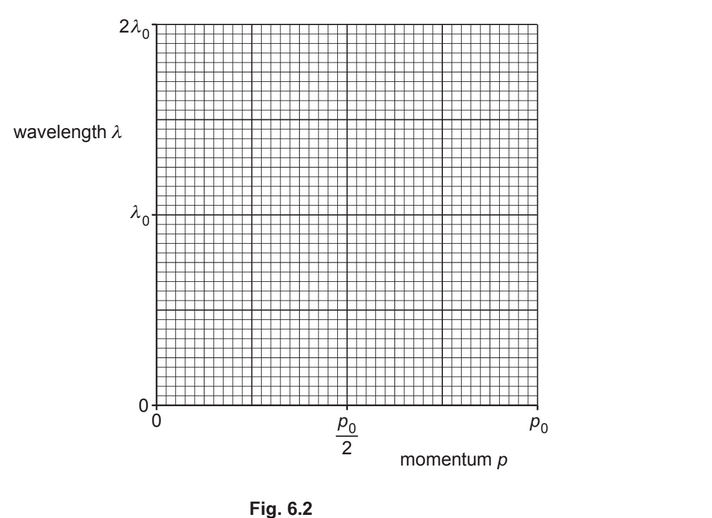
(b) The de Broglie wavelength of a particle is \(λ_ 0\) when its momentum is \(p_0\). On Fig. 6.2, sketch the variation with momentum p of the de Broglie wavelength λ of the particle for values of momentum from \(\frac{p_0}{ 2}\) to \(p_0\).
(c) A radioactive isotope decays with a half-life of 15s to form a stable product.
A fresh sample of the radioactive isotope at time t = 0 contains N0 nuclei and no nuclei of the stable product. On Fig. 6.3, sketch the variation with t of the number n of nuclei of the stable product for time t = 0 to time t = 45s.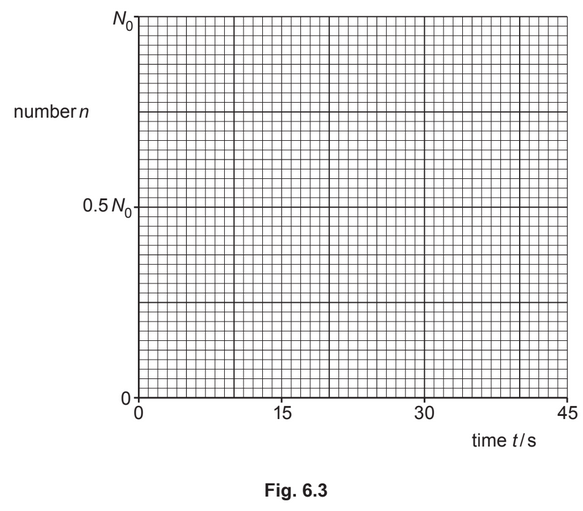
Answer/Explanation
Ans:
(a) from x = 0 to x = r: E = 0
from x = r to x = 3r: curve with negative gradient of decreasing magnitude passing through (r, E0)
line passing through (2r, E0 / 4) and (3r, E0 / 9)
(b) from p =p0 / 2 to p =p0: curve with negative gradient of decreasing magnitude passing through (p0, λ0)
line passing through (1⁄2p0, 2λ0)
(c) from t = 0 to t = 45 s: curve with positive gradient of decreasing magnitude starting at (0, 0)
line passing through (15, 1⁄2N0)
line passing through (30, 0.75N0) and (45, 0.88N0
