Question
(a) Explain what is meant by the binding energy of a nucleus.
…………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………..
(b) The following nuclear reaction takes place:
\(_{92}^{235}\textrm{U} + _{0}^{1}\textrm{n}\rightarrow _{55}^{144}\textrm{Cs} + _{x}^{90}\textrm{Rb} + y_{0}^{1}\textrm{n}\)
(i) Determine the values of x and y.
x = ………………………………………………………
y = ………………………………………………………
(ii) State the name of this type of nuclear reaction.
…………………………………………………………………………………………………………………….
(iii) Compare the binding energy per nucleon of uranium-235 with the binding energy per nucleon of caesium-144.
………………………………………………………………………………………………………………………….
………………………………………………………………………………………………………………………….
(c) Yttrium-90 decays into zirconium-90, a stable isotope.
A sample initially consists of pure yttrium-90.
Calculate the time, in days, when the ratio of the number of yttrium-90 nuclei to the number of zirconium-90 nuclei would be 2.0.
The half-life of yttrium-90 is 2.7 days.
time = ………………………………………… days
Answer/Explanation
(a)
(minimum) energy required to separate the nucleons
to infinity
(b)(i)
X=37
Y=2
(b)(ii)
fission
(b)(iii)
binding energy per nucleon smaller for U than for Cs
(c)
Current ratio 2 Y to 1 Zr, so initially 3 Y
2 = 3 e–λt
λ = 0.693 / 2.7
ln(2 / 3) = – (ln 2 / 2.7)t
t = 1.6 days
or
(½)n = 2 / 3
n = 0.585
time = 0.585 × 2.7
= 1.6
Question
One possible nuclear reaction that takes place is
![]()
Data for nuclei in this reaction are given in Fig. 12.1.
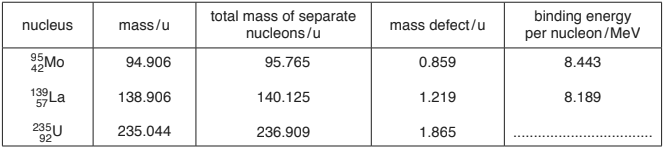
Fig. 12.1
(a) Show that the energy equivalent to a mass of \(1.00\) u is \(934\)MeV.
(b) (i) Use data from Fig. 12.1 to calculate the binding energy per nucleon of a nucleus of uranium-\(235\) \(\left ( _{92}^{235}\textrm{U} \right )\). Complete Fig. 12.1.
(ii) The nucleon number of an isotope of the element rutherfordium is \(267\).
State whether the binding energy per nucleon of this isotope will be greater than, equal to or less than the binding energy per nucleon of uranium-\(235\).
(c) Calculate the total energy, in MeV, released in this nuclear reaction.
(d) The nuclei in \(1.2 \times 10^{–7}\) mol of uranium-\(235\) all undergo this reaction in a time of \(25\) ms.
Calculate the average power release during the time of \(25\) ms.
Answer/Explanation
Ans:
(a) \(E\) = \((3.0 \times 10^{8})^{2} \times 1.66 \times 10^{–27}\) (= \(1.49 \times 10^{–10}\) J)
= \((1.49 ×\times 10^{–10}) / (1.60 \times 10^{–19})\) = \(9.34 \times 10^{8}\) = \(934\) MeV
or
binding energy = \(8.443 \times 95\) [or equivalent using La-\(139\) nucleus]
binding energy / mass defect = \((8.443 \times 95) / 0.859\) = \(934\) MeV
(b) (i) binding energy = \(1.865 \times 934\) (= \(1741.91\) MeV)
binding energy per nucleon = \(1741.91 / 235\)
= \(7.41\) (MeV)
(ii) less (than)
(c) energy = \({(1.219 + 0.859) – 1.865)} \times 934\)
or
energy = \((95 \times 8.443) + (139 \times 8.189) – (235 \times 7.412)\)
= \(199\) MeV
(d) number of reactions = \(1.2 \times 10^{–7} \times 6.02 \times 10^{23}\)
= \(7.22 \times 10^{16}\)
energy release (for one reaction) = \(199 \times 1.60 \times 10^{–13}\) (= \(3.18 \times 10^{–11}\) J)
power = \((7.22 \times 10^{16} \times 3.18 \times 10^{–11}) / (25 \times 10^{–3})\)
= \(9.2 \times 10^{7}\) W
